Числовые ряды. Сходимость ряда. Сумма ряда, страница 4

Пример:

Ряд – .

Получаем 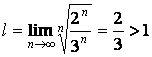– ряд сходится.

7.  Интегральный признак Коши:

, при .

 

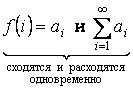
Доказательство:

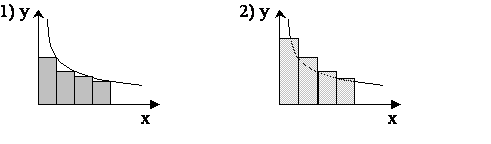
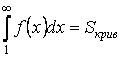 и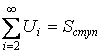 

 

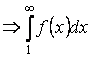Значит, если – сходится  – сходится.

Знакочередующиеся ряды.

Ряды вида: , где .

Теорема Лейбница. Если  и , то ряд 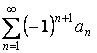 – сходится.

Доказательство:

Пусть , тогда

. При  

.  ограниченна сверху .

Так как  – возрастает и ограниченна сверху

Пример:  – сходится.

Пусть дан ряд , тогда

1)   – сходится, тогда ряд – абсолютно сходится.