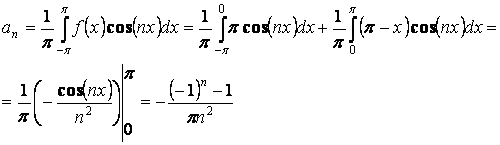
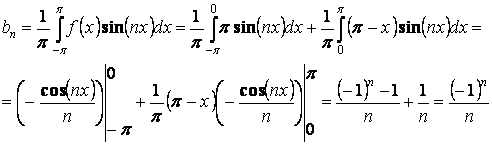
Получаем 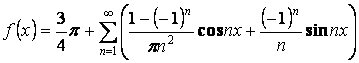
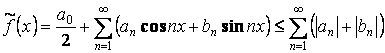
Равенство Парсеваля: 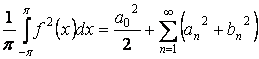
Свойства:
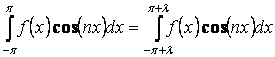
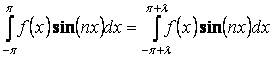
Доказательство:
![]()
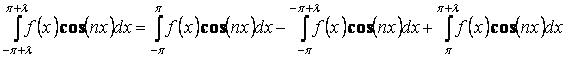
При этом
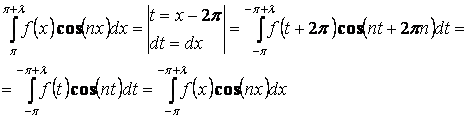
Отсюда получаем
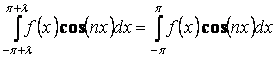
Неполные ряды Фурье.
Ряды от четных и нечетных функций.
Пусть ![]() – четная на
– четная на ![]() , т.е.
, т.е. ![]()
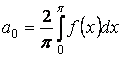
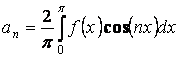
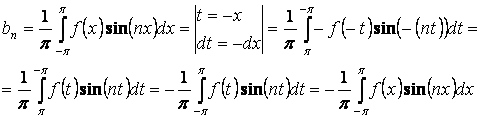
Отсюда ![]() .
.
Пусть ![]() – нечетная на
– нечетная на ![]() , т.е.
, т.е. ![]()
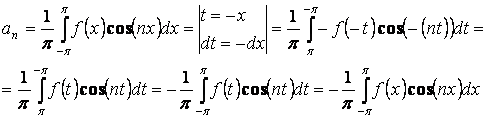
Отсюда ![]() и
и ![]() .
.
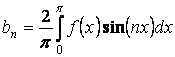
Если функция нечетная, то она раскладывается в ряд по
синусам, т.е. 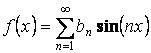 .
.
Если функция четная, то она раскладывается в ряд по
косинусам, т.е. 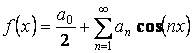 .
.
Ряд Фурье для функции с произвольным периодом.
![]() на отрезке
на отрезке ![]()
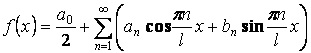
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.