2) ![]() – расходится и
– расходится и ![]() – сходится, тогда ряд сходится
условно .
– сходится, тогда ряд сходится
условно .
Теорема. Если ряд абсолютно сходится, то любая перестановка членов не меняет сумму.
Если ряд сходится условно, то подходящей перестановкой можно сделать его сумму равной любому числу и даже сделать его расходящимся.
Действия над рядами.
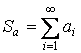 ,
, 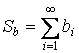 –
абсолютно сходящиеся.
–
абсолютно сходящиеся.
Тогда 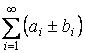 – абсолютно
сходится.
– абсолютно
сходится.
Функциональные ряды.
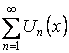 , где
, где ![]() – функция.
– функция.
Область сходимости.
Пусть ![]() фиксировано.
фиксировано.
Тогда 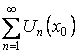 сходится, если
сходится, если ![]() –точка сходимости, и расходится,
если
–точка сходимости, и расходится,
если ![]() – точка расходимости.
– точка расходимости.
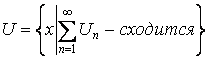 –
область сходимости.
–
область сходимости.
Пример:

![]() ,
то ряд сходится.
,
то ряд сходится.
![]()
![]() ,
где
,
где ![]() – остаток ряда.
– остаток ряда.
Если ряд сходится, то ![]()
Мажорируемые ряды
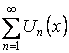 , где
, где ![]() – мажорируемы.
– мажорируемы.
Тогда ![]() – мажоранжа (если
ряд сходится), при
– мажоранжа (если
ряд сходится), при ![]() .
.
Теорема. О непрерывности суммы ряда.
Пусть 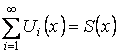 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.