




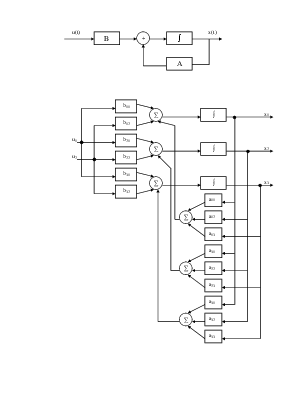

















































1. Римский-Корсаков Б.С. Операционное исчисление. – М.: Высшая школа, 1960.
2. Краснов М.Л., Макаренко Г.И. Операционные исчисления. Устойчивость движения. – М.: Наука, 1964.
3. Солодовников В.В. Основы автоматического регулирования. – М.: ГниМЛ, 1954.
4. Солодовников В.В. Основы автоматического регулирования. – М.: ГниМЛ, 1963.
5. Фельдбаум А.А. Электрические системы автоматического регулирования. Оборонгиз, 1957.
6. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. – М.: Наука, 1974г.
7. Понтрягин Л.С. Математическая теория оптимальных процессов. – М.: Наука, 1983.
8. Воробьёв Л.М., Воробьёва Т.М. Нелинейные преобразования в прикладных вариационных задачах. – М.: Энергия, 1972.
9. Атанс М., Фалб П. Оптимальное управление. – М.: Машиностроение, 1967.
10. Квакерлан Х., Сивал Р. Линейные оптимальные системы управления. – М.: Мир, 1977.
11. Новогранов Б.Н. Расчет частотных характеристик нелинейных автоматических систем. – М.: Машиностроение, 1986.
12. Палис Ж., Дименц В. Геометрическая теория динамических систем. – М.: Мир, 1986.
13. Месарович М., Токахара Я. Общая теория систем: математические основы – М.: Мир, 1978.
14. Крутько П.Д. Обратные задачи динамических управляемых систем.
15. Топчеев Ю.И. Атлас для проектирования систем автоматического регулирования. – М.: Машиностроение, 1988.
16. Справочник по теории автоматического управления. /под ред. А.А. Красовского – М.: Наука, 1987.
17. Бендриков Г.А., Теодорник К.Ф. Траектории корней линейных автоматических систем – М.: Наука,1964.
Автоматы в современных технических системах применяются в основном для выполнения рутинных операций (автопилот), выполнения точных операций, выполнения динамических операций, выполнения операций в опасных для человека условиях.
Задачи теории управления:
1. Создание методов анализа, позволяющих определить соответствие системы предъявленным требованиям;
2. Создание методов синтеза, позволяющих конструировать исходя из заданных требований;
3. Создание методов экспериментального исследования и испытаний.
Теория управления представляет собой научную дисциплину, которая изучает различные явления без учета их конкретной естественной природы, основываясь на формальных взаимосвязях между составляющими факторов и их изменениях под влиянием внешних воздействий. Результатом исследования является характер взаимодействия и функционирования, а не конкретное взаимодействие с вовлеченными во взаимодействие механизмами.
Определение системы:
Системой будем называть формальную взаимосвязь между наблюдаемыми признаками и их свойствами.
 |
 Первые технические реализации автоматического управления были
реализованы в 1765 году Ш.И. Пензуковым для регулирования уровня воды в паровом
котле и в 1784 английским механиком Уаттом для регулирования паровой машины.
Первые технические реализации автоматического управления были
реализованы в 1765 году Ш.И. Пензуковым для регулирования уровня воды в паровом
котле и в 1784 английским механиком Уаттом для регулирования паровой машины.
Теория систем развивалась профессором И.А. Вишнеградским 1876 г. "Общая теория регуляторов". По заданию Максвелла Раус вывел условия устойчивости 1909 г. Н.Е. Жуковский "Теория регулирования хода машин".
Конец XIX века А.М. Ляпунов - первый и второй методы для нелинейных систем. Частотные методы А.В. Михайлова 1938 г.
1) Системой S называется отношение
на непустых абстрактных множествах ![]() где множество Vi - объект системы. Если I
конечно то
где множество Vi - объект системы. Если I
конечно то ![]()
2) Пусть ![]() и
и ![]() образуют
разбиение множества I.
образуют
разбиение множества I.
![]() - условие
полноты;
- условие
полноты;
![]() - условие
единственности;
- условие
единственности;
![]() - входные объекты или вход;
- входные объекты или вход;
![]() - выходные объекты или выход;
- выходные объекты или выход;
![]() - система вход-выход (черный ящик).
- система вход-выход (черный ящик).
Если Vi являются функциями
времени и пространства то система динамическая. Vi
в основном представляются в виде мультипликации параметра ai
и переменной xi ![]() .
.
Если параметр ai не зависит от времени и пространства, то система будет с постоянными параметрами.
Если ai является функцией пространства, то система называется с распределенными параметрами.
Если ai является функцией времени, то система называется с распределенными параметрами.
Для того чтобы служить различным целям в различных конкретных системах теория движения удовлетворяет предельно общему и чисто математическому подходу.
Нами в подходе будут использованы следующие принципы:
1. аксиоматическое введение понятий с самым строгим исследованием поведения;
2. одинаковое отношение как к системам целенаправленного поведения так и к системам преобразующим входные величины в выходные;
3. математические структуры, обеспечивающие формализацию основных отношений, должны обеспечивать строгость и общность утверждений.
Определение и основные свойства линейного пространства
Пусть V - множество элементов с двумя операциями:
а) сложение элементов множества;
б) умножение элементов множества на число.
Аксиомы:
Если ![]()
Если ![]()
Следствия или свойства
Свойство 1: Сложение векторов коммутативно ![]() .
.
Свойство 2: Сложение векторов ассоциативно ![]() .
.
Свойство 3: Существует хотя бы один элемент ![]() .
.
Свойство 4: Для всякого элемента ![]() существует
хотя бы один
существует
хотя бы один ![]() .
.
Свойство 5: Существует хотя бы один элемент ![]()
Описание состояния системы
Возьмем список величин (скалярных) ![]()
![]()
![]() .
Введем систему векторов
.
Введем систему векторов ![]()
![]()
Система векторов ![]() называется
линейно-независимой или базисом, если
называется
линейно-независимой или базисом, если 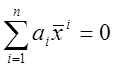 справедлива
только при ai=0 iÎJ={1¸N}.
справедлива
только при ai=0 iÎJ={1¸N}.
Рассмотрим систему уравнений
a11x1+a12x2+…+a1nxn+ b11u1+b12u2+…+b1mum=0
a21x1+a22x2+…+a2nxn+ b21u1+b22u2+…+b2mum=0
an1x1+an2x2+…+annxn+ bn1u1+bn2u2+…+bnmum=0
Которую в матричной форме можно записать:
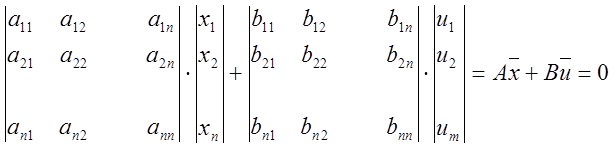
Это алгебраическая система линейных уравнений, которые связывают вектор
зависимых переменных (состояний) ![]() и вектор
независимых или произвольных переменных
и вектор
независимых или произвольных переменных ![]() (управлений).
(управлений).
Решение такой системы уравнений известно ![]() и
требует несингулярнотси матрицы А.
и
требует несингулярнотси матрицы А.
Рассмотренные уравнения инвариантно по времени.
Разрушим эту инвариантность, потребовав ![]() -
форма Коши, т.е. сделав
-
форма Коши, т.е. сделав ![]() (t)
– функцией времени, а систему динамической.
(t)
– функцией времени, а систему динамической.
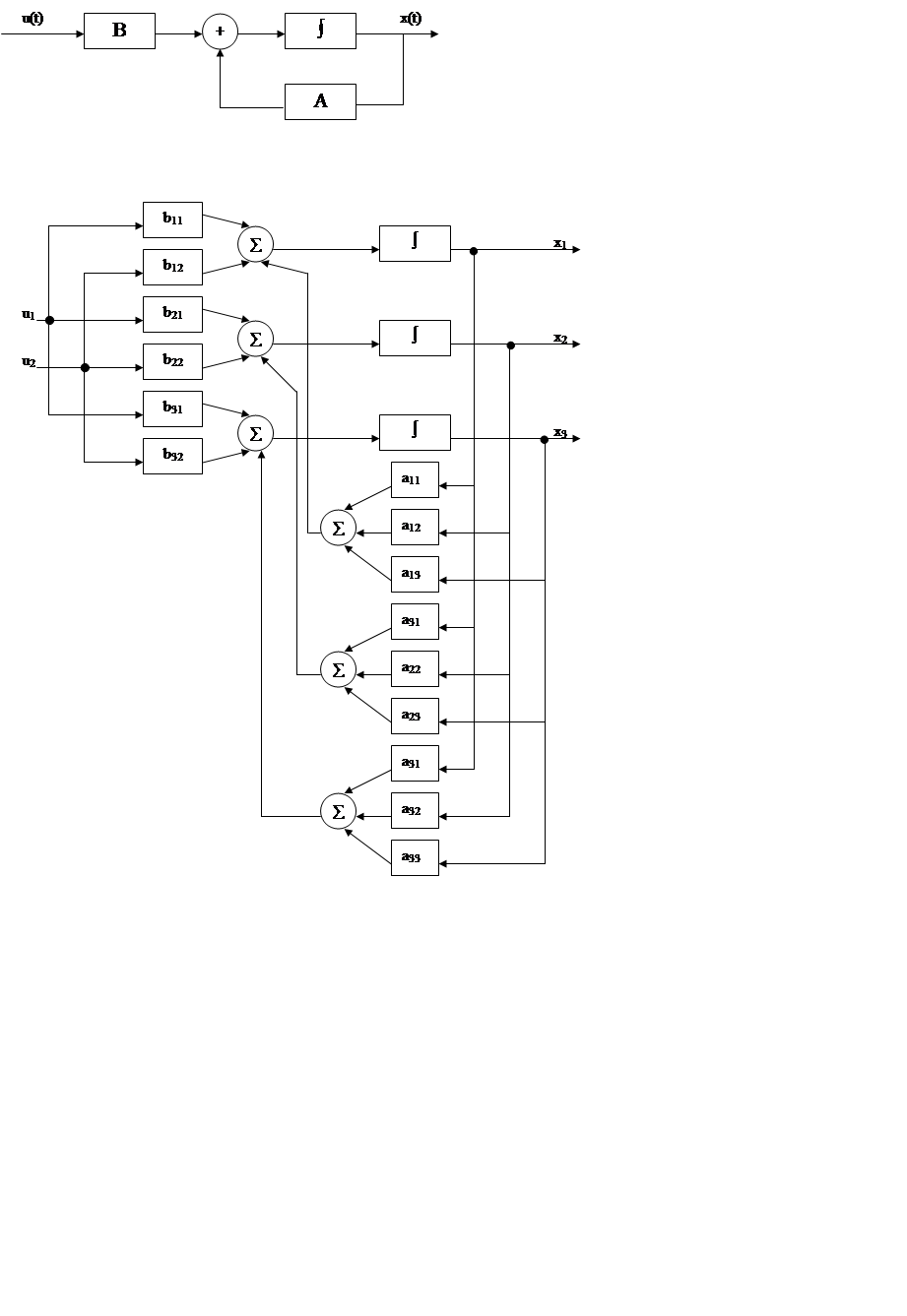 |
![]() - вектор состояния;
- вектор состояния;
![]() – уравнение состояния;
– уравнение состояния;
![]() - вектор управления;
- вектор управления;
![]() - уравнение выхода;
- уравнение выхода;
![]()
![]() -
переходная функция.
-
переходная функция.
В общем случае система может быть описана системой дифференциальных уравнений:
![]() – состояние
– состояние
![]() – выход
– выход
![]() – переходная функция
– переходная функция
Линеаризация
1) Пусть имеем динамическую систему
![]()
![]() где
где ![]()
![]()
![]()
![]() и
и ![]() –
матрицы Якоби
–
матрицы Якоби
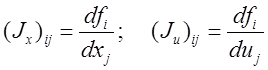
![]() – начальное условие
– начальное условие
2) Конечные разности
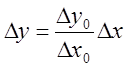
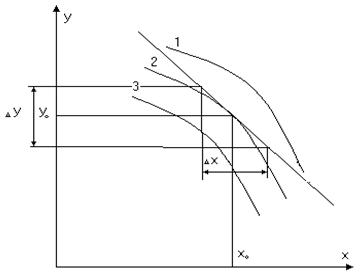 |
3)
![]()
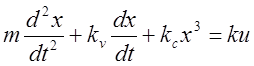
![]()
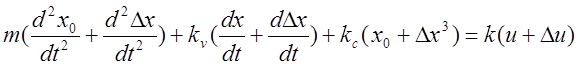
![]()
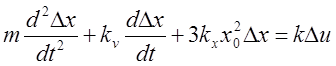
4) Метод наименьших квадратов
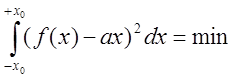
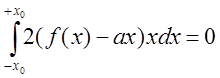
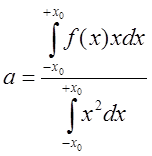
5) Гармоническая линеаризация
Класс существенно нелинейных элементов можно разделить на группы:
а) однозначные нелинейности ![]()
б) многозначные нелинейности 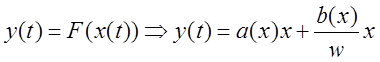
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.