Лекция № 10
ПРИНЦИП МАКСИМУМА
В ряде практических задач оптимизации объектов
управления экстремум функционала (3.91) при заданных уравнениях объекта (3.92)
обеспечивается при управлении u(t), имеющем разрывы первого рода. При этом
координаты ![]() также имеют разрывы, положение и
число которых заранее неизвестны. Эти обстоятельства затрудняют применение
классического вариационного исчисления для некоторых задач оптимизации, которые
могут быть решены методом, разработанным акад. Л.С.Понтрягин и названным
принципом, максимума.
также имеют разрывы, положение и
число которых заранее неизвестны. Эти обстоятельства затрудняют применение
классического вариационного исчисления для некоторых задач оптимизации, которые
могут быть решены методом, разработанным акад. Л.С.Понтрягин и названным
принципом, максимума.
Задачай оптимизации является определение оптимальных управлений u°(t) и траектории Х°(t) из условия минимума функционала (3.91) для заданных уравнений объекта (3.92) при начальных X(t0) и конечных X(tк) значениях, заданном интервале времени t0 £ t £ tк с учетом ограничений вида X(t) Î Wx, u(t) Î Wu .
Функции управления u(t) допускают разрывы первого рода (см. кривую 1 на рис. 3.6). Так как координаты выхода xi(t) не являются гладкими, то канонические уравнения (3.78) и (3.80) при введенных множителях Лагранжа (3.76) и функции Гамильтона (3.77) не могут быть непосредственно применены для определения оптимальных управлений. Объясняется это тем, что из-за разрывов первого рода вариация функции u(t) может быть большой, следовательно, большой будет и вариация функционала. В результате этого в выражении (3.56) уже нельзя ограничиваться только линейными относительно вариаций функций du(t) и dх(t) членами, а следует учитывать также нелинейные члены. В связи с этим было введено понятие игольчатой вариации [12].
Игольчатая вариация представляет собой приращение варьируемой функции оптимального управления u°(t) на бесконечно малом отрезке времени e в виде импульса ограниченной величины (см. кривую 4 на рис. 3.6) с учетом u(t) Î Wu. Влияние такой вариации на последующее движение объекта управления в интервале t < t < tк бесконечно мало, поскольку влияние любого импульса оценивается величиной его площади (u – u°) е, которая в данном случае бесконечно мала. Следовательно, приращение функционала при игольчатой вариации управления будет бесконечно малым. Оно обращается в нуль, т. е. выполняется условие экстремума (3.58) функционала (3.54), когда игольчатая вариация производится относительно оптимального управления u°(t).
Основные уравнения и их применение для синтеза оптимальных систем. Рассмотрим кратко сущность принципа максимума. Пусть математическая модель объекта оптимизации задана в виде уравнений состояния
![]() , (3.113)
, (3.113)
где i = 1, 2, ..., n; r – количество координат управления. Уравнение (3.113) можно представить в векторной форме
![]() . (3.114)
. (3.114)
Сигналы управления могут иметь ограничения для всех координат
![]() .
.
Зададимся некоторой функцией f0(Х, u) и будем считать, что цель управления объектом будет достигнута, если изображающая точка из начального положения Х0 с координатами (х10, х20, ..., хn0) в n-мерном фазовом пространстве переместится в положение Х1 с координатами (x11, x21, …, xn1).
При оптимизации объекта требуется найти вектор управляющего воздействия u(t) с учетом указанных ограничений из условия минимума функционала
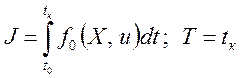 . (3.115)
. (3.115)
Сначала рассмотрим задачу при одной координате управления (r=1) в пространстве (n+1) координат, введя дополнительную переменную х0, определяемую уравнением
![]() . (3.116)
. (3.116)
При этом для вывода принципа максимума используем игольчатую вариацию.
Если управляющему воздействию u°(t) соответствует оптимальное движение объекта Х°(t), то после игольчатой вариации дальнейшее движение X(t) будет отличаться от оптимального. Разность между ними в момент t=t , определяется разностью скоростей
![]() . (3.117)
. (3.117)
Эта разность бесконечно мала, так как e – бесконечно малая величина. Поэтому для интервала t £ t £ T введем вектор вариации траектории
![]() .
.
Закон изменения вариации, являющейся бесконечно малой величиной, может быть найден из уравнений, записанных для малых изменений X(t), которые называют уравнениями в вариациях. Эти уравнения можно получить из (3.113) или (3.114), если заменить xi на xi + dхi а затем после разложения fi в ряд по степеням dxi отбросить члены высших порядков малости. Далее вычтем уравнение вида (3.113) и получим линейное уравнение в вариациях
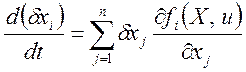 , (3.118)
, (3.118)
где j = 0, 1, 2..., n.
Вектор вариаций dX при t = Т характеризует изменение критерия оптимальности dJ. Для любых неоптимальных управлений u(t) эта величина определяется скалярным произведением вектора вариаций dX(T) и вспомогательного вектора y(Т) и является отрицательной:
![]() . (3.119)
. (3.119)
Уравнение (3.119) позволяет найти dX(T) в зависимости от начального условия dX(t), определяемого значением u(t).
Если подобрать такой (n+1)-мерный вектор y(t), который при t < t £ T удовлетворяет условию
![]() , (3.120)
, (3.120)
где y(t) = [y0(t) y1(t) … yn(t)]T,
то вместо принятой в классическом вариационном исчислении функции Гамильтона (3.77) можно составить функцию Гамильтона для неклассических вариационных задач:
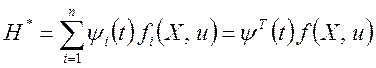 . (3.121)
. (3.121)
Эта функция достигает максимума при оптимальном управлении u°(t), откуда следует принцип максимума: нужно так подобрать u(t) Î Wu, чтобы величина Н* достигала максимального значения. При этом можно записать (для открытого множества Wu)
¶Н*/¶u = 0. (3.122)
Используя выражение (3.121) и уравнения объекта управления (3.113) с учетом (3.116), можно составить аналогично уравнениям (3.81) канонические уравнения Гамильтона для неклассических вариационных задач:
![]() , (3.123)
, (3.123)
где i = 0, 1, 2, ..., n.
Уравнения (3.123) при r координатах управления дополняются уравнениями
![]() . (3.124)
. (3.124)
Пусть существует допустимое управление u(t) Î Wu, то соответствующая ему фазовая траектория проходит через фиксированные начальную X(t0) и конечную X(Т) точки. Тогда u°(t) определяется по теореме Л. С. Понтрягина [12]:
для того чтобы управление u(t) было оптимальным, необходимо существование такой ненулевой вектор-функции y(t), соответствующей в силу уравнений (3.123) функциям u(t) и X(t), чтобы:
1) при t0 £ t £ Т функция H* достигла максимума при u°(t)
![]() ; (3.125)
; (3.125)
2) в конечный момент времени t = Т выполнялись бы соотношения
![]() . (3.126)
. (3.126)
В большинстве случаев в (3.126) можно принять y0(Т) = – 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.