![]()
|
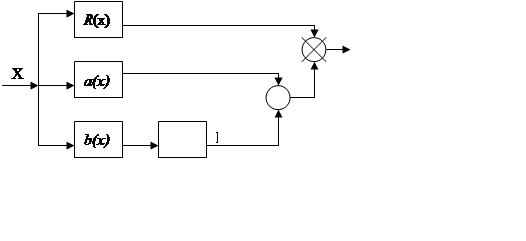
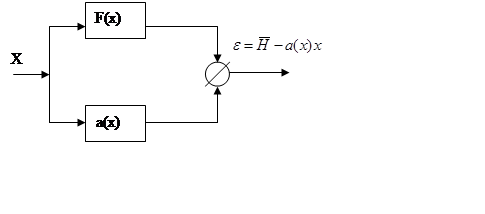
Минимизация
ошибки 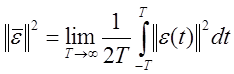
Среднее значение
квадрата разности, где ![]()
В общем случае
![]()
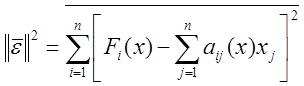 - алгебра.
- алгебра.
Для определения ![]()
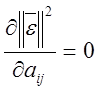 (см.
в конце)
(см.
в конце)
Пример. Система управления перевернутого маятника.
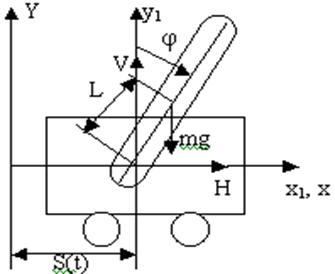 S(t) – линейное положение
S(t) – линейное положение
φ(t) – угловое положение
m – масса маятника
М – масса тележки
Н – горизонтальная сила реакции
V – вертикальная сила реакции
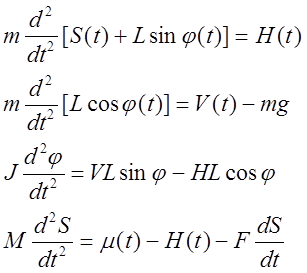
Предположим, что H(t)≈0, т.к. m<<M и φ- мал.
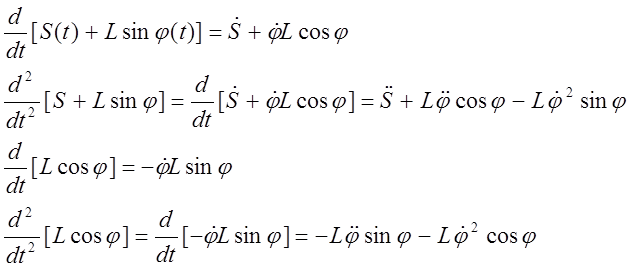
Тогда система уравнений имеет вид:
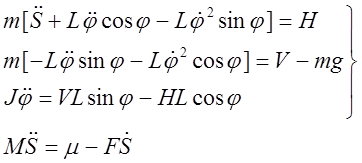
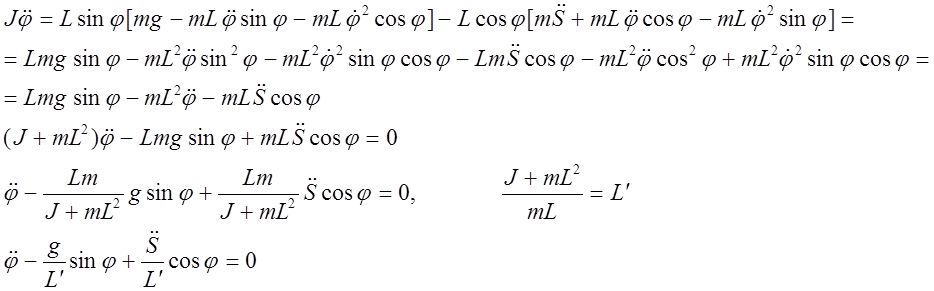
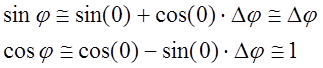 Линеаризация:
Линеаризация:
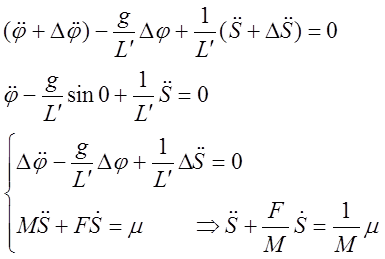
- согласно исходному уравнению
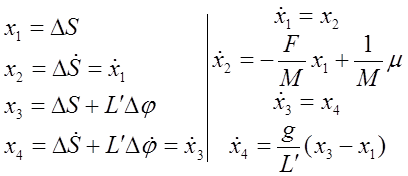
В окончательном виде:
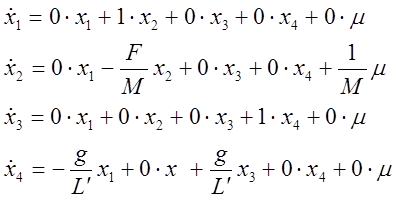
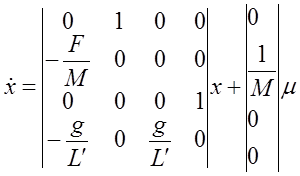 F/M=1 сек-1 1/М=1 кг-1
F/M=1 сек-1 1/М=1 кг-1
g/L’=11,65 сек-2 L’=0,482 м.
Пример: Смесительный бак.
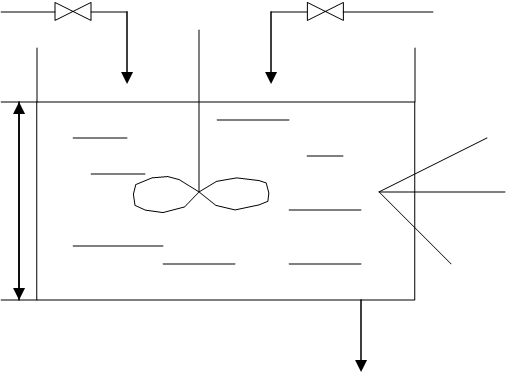 Расход F1 Расход
F2
Расход F1 Расход
F2
Конц. С1 Концентрация С2
V – объем
h С - концентрация
S - площадь
Расход F
Концентр. С
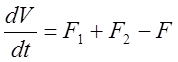 .
.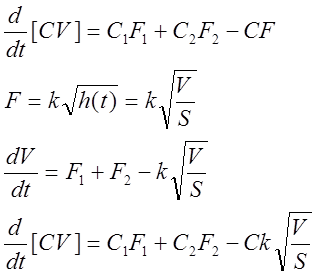
Установившееся состояние
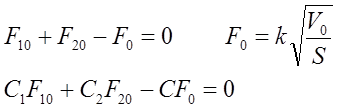
Пусть F1=F10+f1
F2=F20+f+2
V=V0+v
C=C0+ξ
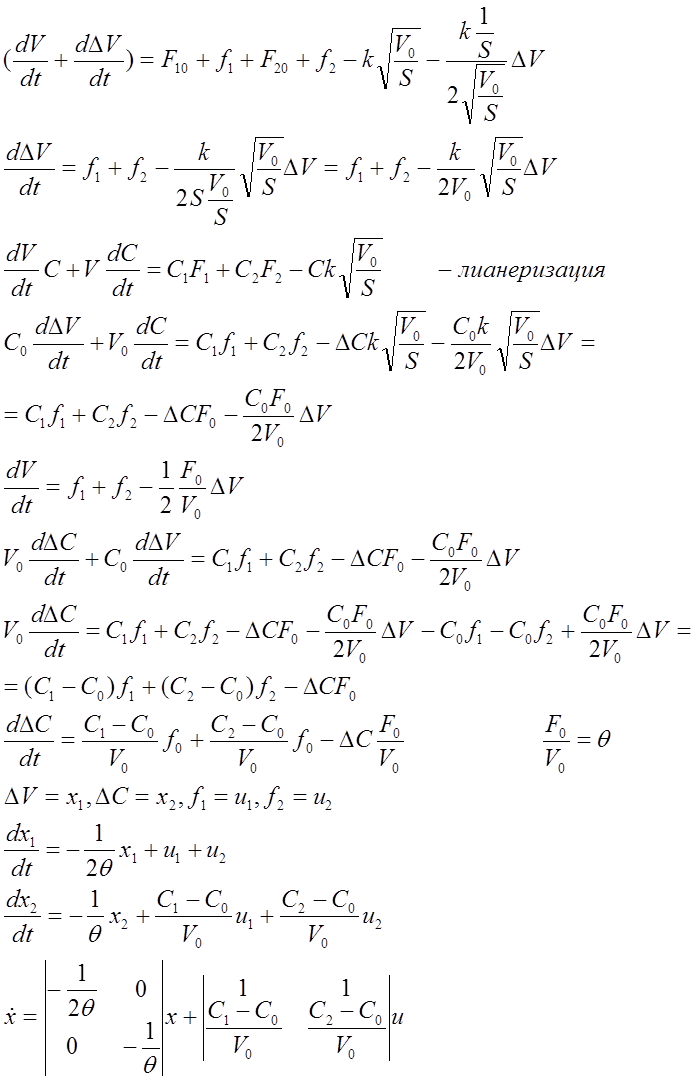
Пусть 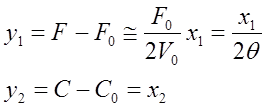
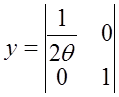 F10=0,015 м3/сек С1=1
кмоль/м3
F10=0,015 м3/сек С1=1
кмоль/м3
F20=0,005 м3/сек С2=2 кмоль/м3
F0=0,02 м3/сек С0=1,25 кмоль/м3
V0=1 м3 θ=50 сек
![]() - уравнение состояния.
- уравнение состояния.
Теорема 1. Для однородного уравнения ![]() , где А – постоянная величина,
для всех t всегда существует решение,
, где А – постоянная величина,
для всех t всегда существует решение,![]() .
.
Переходная матрица ![]() является решением
матричного дифференциального уравнения:
является решением
матричного дифференциального уравнения:
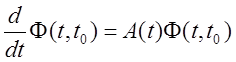 для всех t.
для всех t.![]() .
.
Теорема 2. Переходная матрица ![]() линейной
дифференциальной системы имеет следующие свойства:
линейной
дифференциальной системы имеет следующие свойства:
1) ![]() ,
, ![]() ;
;
2) ![]() - неособая для всех
- неособая для всех ![]() ;
;
3) ![]()
![]()
4) 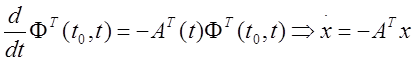 - сопряженная система.
- сопряженная система.
Доказательство.
![]()
![]()
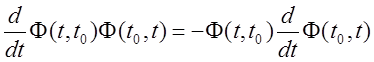
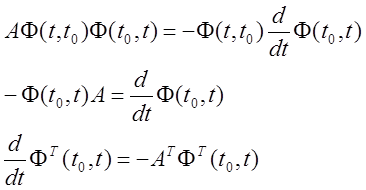
Теорема 3. Для линейного неоднородного дифференциального уравнения
![]() где B(t) и u(t) –
кусочно-непрерывные функции, решение имеет вид
где B(t) и u(t) –
кусочно-непрерывные функции, решение имеет вид
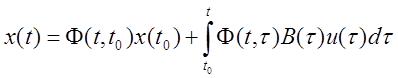
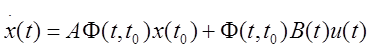
Рассмотрим систему с выходной переменной y=Cx.
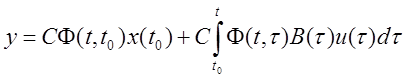
Если ![]() , то
, то 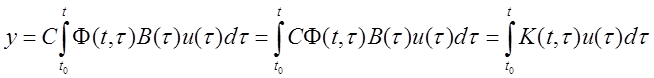
![]() импульсная переходная функция.
импульсная переходная функция.
Экспонента от ![]()
![]()
![]()
![]() или
или ![]()
Почему
использовали термин “ Экспонента от ![]() ”?
”?
![]()
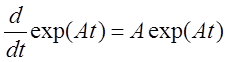
![]()
4. Решение
уравнения ![]() при
при ![]() имеет
вид:
имеет
вид:
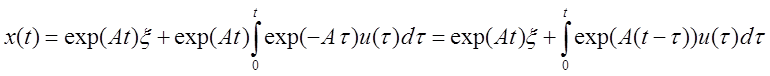
Далее
эвристически покажем, что ![]() можно
рассматривать как бесконечный ряд
можно
рассматривать как бесконечный ряд
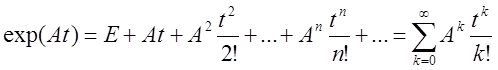
1.
При ![]()
![]()
2. При почленном дифференцировании имеем:
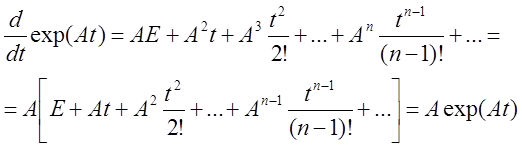
Устойчивость линейных систем с постоянными параметрами
Рассмотрим ![]() где
где ![]() ). Система устойчива, если малые отклонения от
положения равновесия, т.е. решения
). Система устойчива, если малые отклонения от
положения равновесия, т.е. решения ![]() остаются малыми
при сколь угодно большом увеличении времени и наоборот система неустойчива,
если малые отклонения становятся сколь угодно большими.
остаются малыми
при сколь угодно большом увеличении времени и наоборот система неустойчива,
если малые отклонения становятся сколь угодно большими.
![]()

Система![]() устойчива, если евклидова норма
устойчива, если евклидова норма ![]() остается ограниченной при
остается ограниченной при ![]() , т.е. для любого
, т.е. для любого ![]() и
и ![]() существует
существует
![]() , такое что
, такое что ![]() ,
то
,
то ![]() для
для ![]() .
.
Решение является асимптотически или абсолютно устойчивой, если ![]()
Решение является экспоненциально устойчивым, если ![]()
![]()
Устойчивость линейных систем с постоянными параметрами
![]()
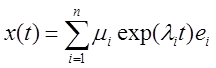 где
где
![]() - собственные векторы,
- собственные векторы, ![]() – скаляры,
определяемые через
– скаляры,
определяемые через ![]() .
.
Линейная система ![]() является
устойчивой в смысле Ляпунова тогда и только тогда, когда все характеристические
числа матрицы А имеют неположительные действительные части, и любому
характеристическому числу на мнимой оси кратности m
точно соответствует m собственных векторов матрицы А.
является
устойчивой в смысле Ляпунова тогда и только тогда, когда все характеристические
числа матрицы А имеют неположительные действительные части, и любому
характеристическому числу на мнимой оси кратности m
точно соответствует m собственных векторов матрицы А.
Задачи операционного исчисления.
 |
Операционное исчисление Лапласа.
Оригинал и изображение.
Оригинал – любая
функция![]() действительного аргумента t, удовлетворяющая условиям:
действительного аргумента t, удовлетворяющая условиям:
а) кусочно - непрерывности за исключением конечного числа точек разрыва первого рода;
б) ![]()
![]()
в) существуют ![]() ,
, ![]() такие,
что для всех t
такие,
что для всех t ![]()
Изображение: 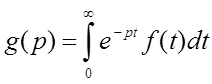
![]() или
или 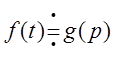
Пример.
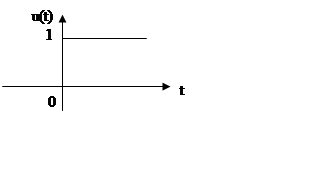
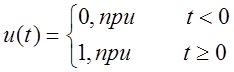
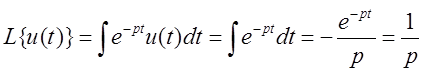 , при
, при ![]() .
.
Пример.
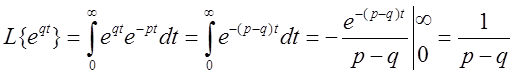
Пример.
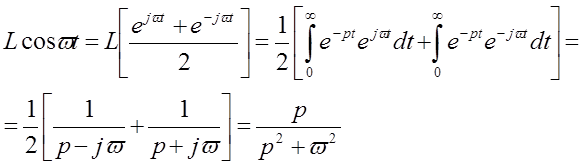
Теорема:
Изображение ![]() оригинала
оригинала![]() определено в полуплоскости
определено в полуплоскости ![]() , где
, где ![]() –
показатель роста оригинала.
–
показатель роста оригинала.
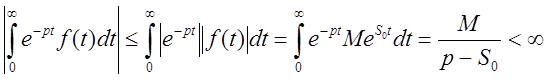
Действительная и мнимая части изображения
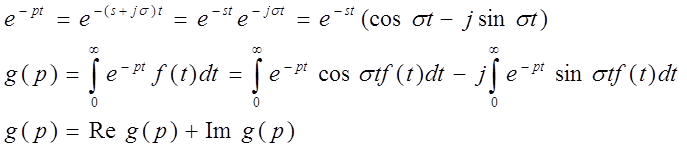
Линейность: ![]() ;
; ![]() =>
=>
![]()
Подобие: ![]() и
и ![]() то
то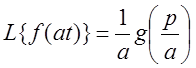
Запаздывание:
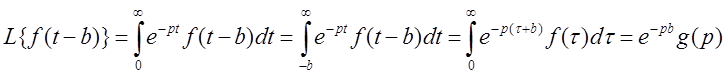
Пример
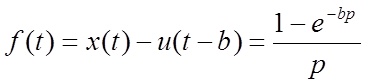
Система с
постоянными параметрами ![]() является
асимптотически устойчивой тогда и только тогда, когда все характерные числа
матрицы А имеют строго отрицательные действительные части.
является
асимптотически устойчивой тогда и только тогда, когда все характерные числа
матрицы А имеют строго отрицательные действительные части.
Дифференцирование оригинала
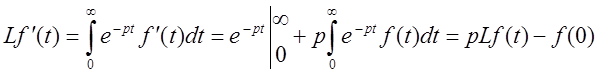
Интегрирование оригинала
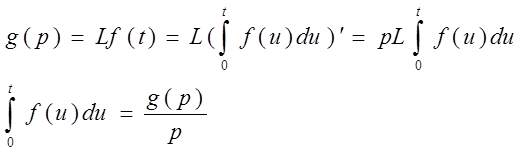
Формула обращения
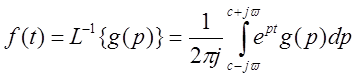
Изображение 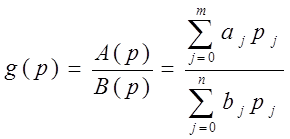 ;
; ![]()
Корни
знаменателя ![]() , являющиеся полюсами
дробно-рационального изображения
, являющиеся полюсами
дробно-рационального изображения ![]() ,Суть
,Суть ![]() с кратностями
с кратностями ![]() . Если
. Если ![]() ,
, ![]() ,
то
,
то
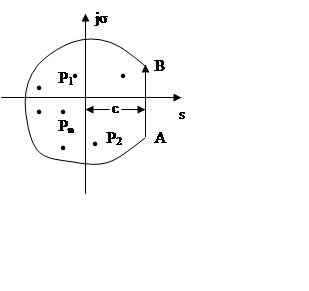
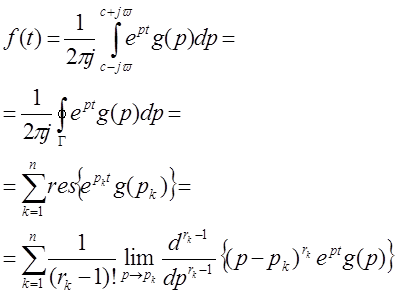
Теорема:
если изображение 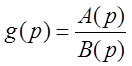 является
дробно-рациональной функцией со степенью числителя меньше степени знаменателя,
имеющего корни
является
дробно-рациональной функцией со степенью числителя меньше степени знаменателя,
имеющего корни ![]() кратности
кратности ![]() , то оригинал определяется следующим
(см. выше) образом.
, то оригинал определяется следующим
(см. выше) образом.
Следствие:
Если 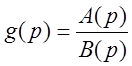 , где корни простые, то
, где корни простые, то 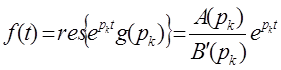
Пример 1:
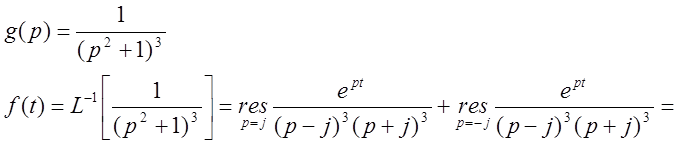
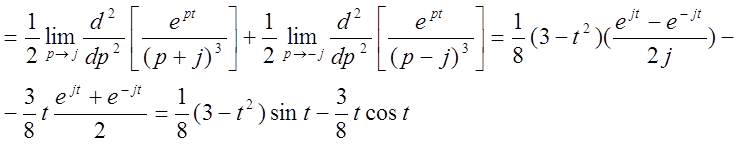
Пример 2:
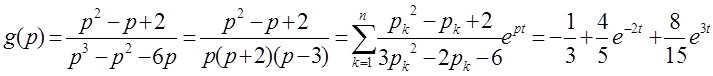
Анализ систем с постоянными параметрами на основе преобразования Лапласа
Решение дифференциального уравнения состояния.
![]()
![]()
![]()
Теорема: Пусть матрица системы А является
постоянной матрицей размерности ![]() тогда
тогда ![]() или
или ![]() где
где
![]() резольвента матрицы А.
резольвента матрицы А.
Рассмотрим постоянную матрицу А,
размерности ![]() с характеристическим полиномом
с характеристическим полиномом 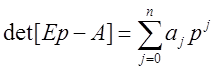 тогда
тогда 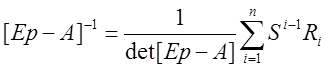 где
где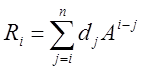
![]()
![]()
![]()
Пусть ![]() тогда
тогда
![]() при
при ![]() имеем
имеем
![]() или
или ![]() где
где
![]() - матричная передаточная функция
системы.
- матричная передаточная функция
системы.
Пример 1.
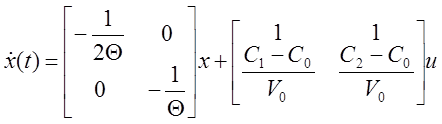
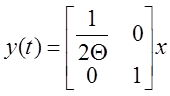
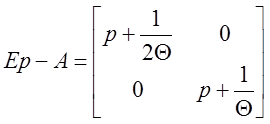
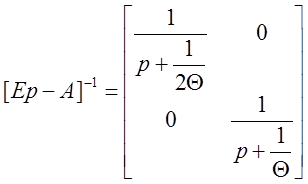
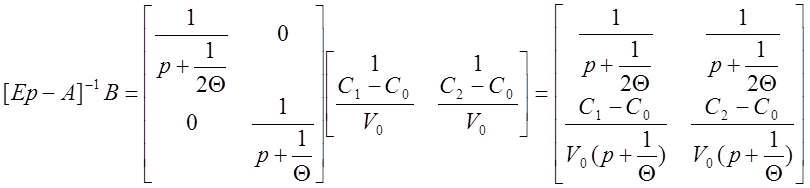
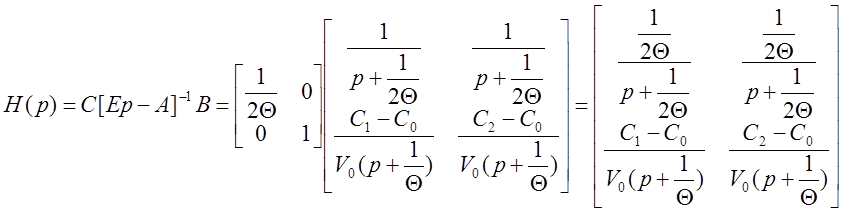
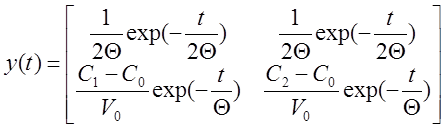
Теорема о конечном значении
![]()
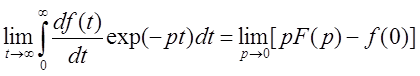
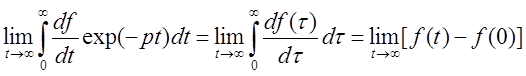
Теорема о наименьшем значении
![]()
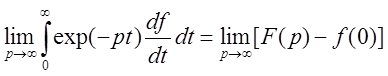
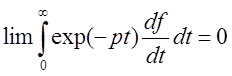
![]()
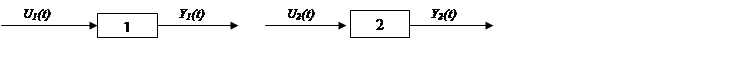
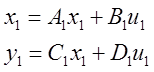
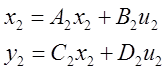
Введем расширенный вектор состояния
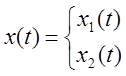
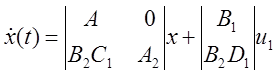
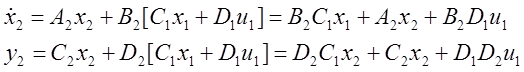
Если ![]()
![]() ,
,
то ![]()
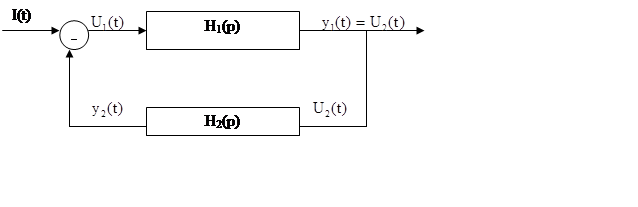
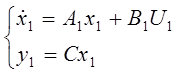 (1)
(1) 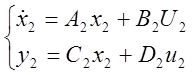 (2)
(2)
Cистема (1) не имеет прямой связки, что позволяет избежать неявных алгебраических уравнений.
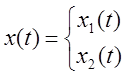
![]()
![]()
![]()
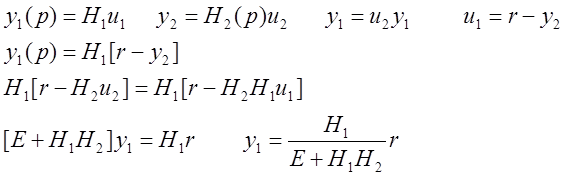
![]() – матрица возвратной разности
– матрица возвратной разности
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.