Применение автоматов в современных технических системах, страница 6

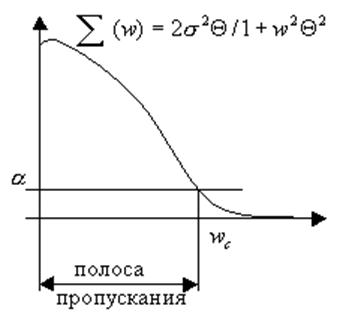
Если  то  называется частотой среза. При =0,01 определяют  как 1% частоту среза.

Определение: Пусть r скалярный процесс со спектральной плотностью энергии . Полоса частот  определяется как  и содержит заданную часть  половины энергии процесса .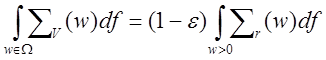

Если , то говорят об 1% частоте среза, что означает содержание в интервале  99% от половины энергии процесса.

Для получения малого (квадрата ошибки) необходимого чтобы полоса пропускания частот системы содержала как можно большую часть полосы пропускания системы.

Рассмотрим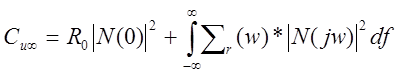

Для получения малого  нужно иметь  в полосе частот эталонной переменной.

Следцет отметить что это не означает что  малая величина, т.к. этот член определяет постоянную часть эталонной переменной, т.е от заданной рабочей точки во входной переменной. Второй член важен для динамического диапазона входной переменной и поскольку этот диапазон ограничен, то входная величина должна быть ограничена тоже.

Однако принципы проектирования  и  - противоречивы. Систему можно спроектировать так, чтобы удовлетворялся один из принципов.

           

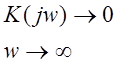
Выберем :

Если  при  то это означает, что  при  должно увеличиваться, а это означает, что  остается большим в частотном диапазоне входного сигнала  . Это приводит к перегрузке системы.

Задача синтеза регулятора, основаная на частотных методах.

Порядок решения:

1.  Составляют математическое описание объекта.

2.  Выбирают регулирующий орган и силовой привод, усилитель и датчики.

3.  Составляют передаточные функции и строят ЛАФЧХ и ФЧХ.

4.  По заданным требованиям на частотные характеристики строят желаемые частотные характеристики ЛАФЧХ и ФЧХ.

5.  По построенным желаемым и действительным частотным характеристикам определяют тип и место введения корректирующих устройств.

Корректирующие устройства бывают последовательные, параллельные и комбинированные.

Последовательные корректирующие устройства достаточно просты, но их включение всегда приводит к увеличению частоты среза и следовательно полосы пропускания системы при  , т.е. когда .

При этом приходится применять более быстодействующие приводы и большим потреблением мощности.

Параллельные корректирующие устройства более сложные, но они сужают полосу пропускания.

В сложных системах применяют как пораллельные, так и последовательные методы.

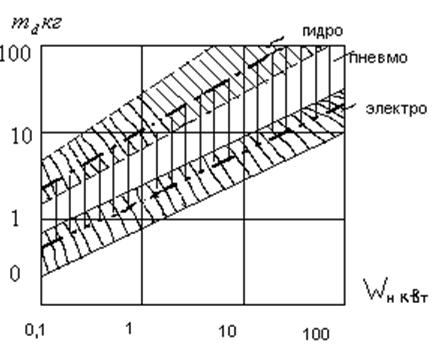
Выбор характеристик двигателя.

Зависимость массы и номинальной выходной мощности.

Выбор механической передачи

-момент инерции ротора

момент инерции якоря двигателя

.

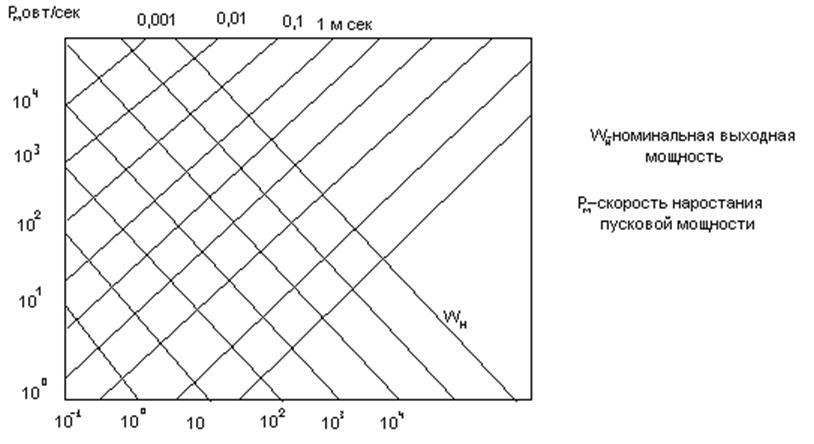
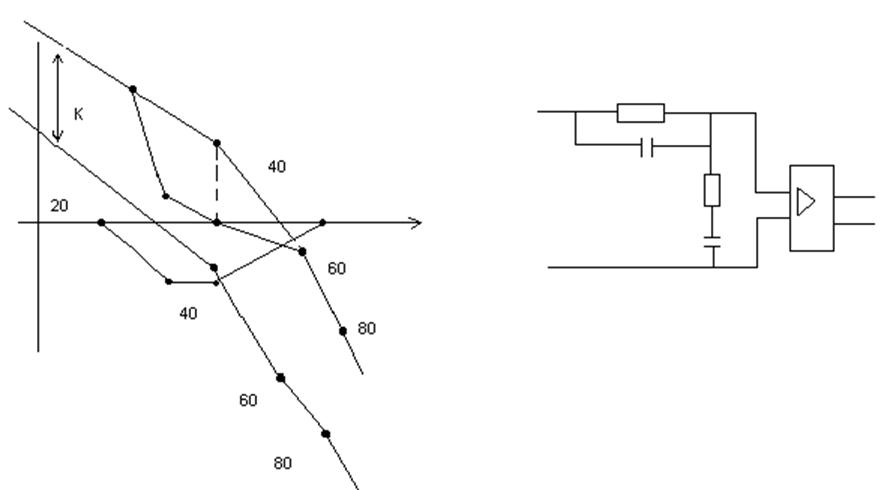
Синтез последовательных и параллельных корректирующих устройств.

                             

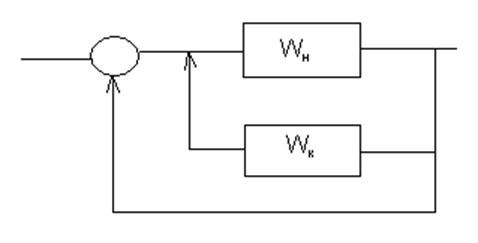
Синтез параллельного устройства

 

                                                  

                         

Влияние возмущений

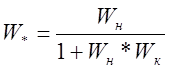
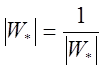
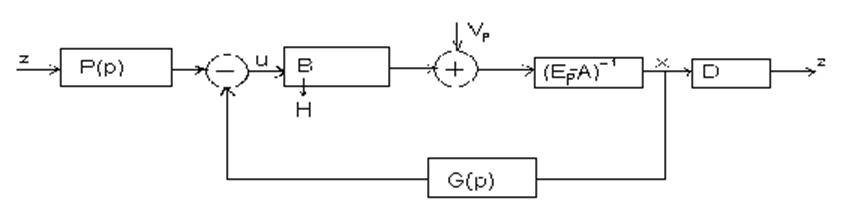
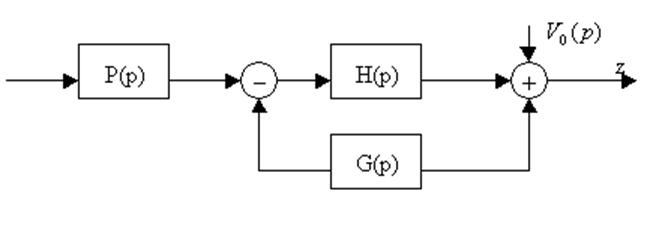
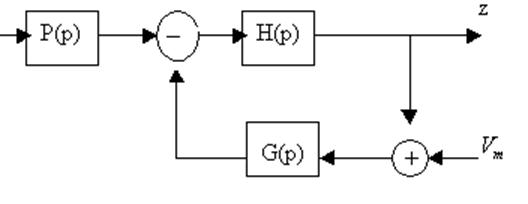
Возмущения, действующие на систему ухудшают показатели качества регулирования.

Исследуем зависимость возрастания квадрата ошибки слежения и квадрата входной переменной за счет действия возмущений и сформулируем принципы проектирования.

Примем допущения:

1.  -процесс не корректированный с  и .

2.  Управляемая переменная является наблядаемой , .

3.  Система управления является ассимптотически устойчивой.

4.  Входная и управляемая переменная является скалярными и  и .

5. 

  :

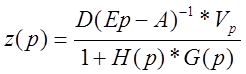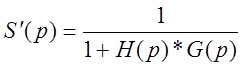
 – неособая матрица.

Составляющая от постоянной части возмущений в установившемся среднем значении квадрата ошибки слежения : 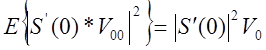 ,    , где - момент второго порядка от .

Составляющая от переменной части возмущений :

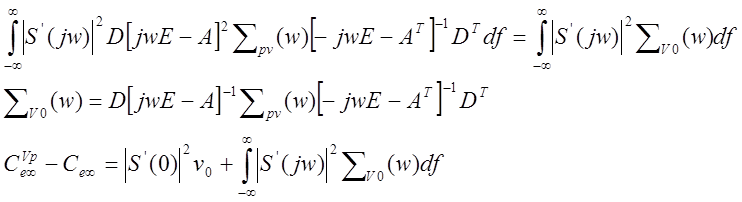
- среднее значение квадрата ошибки слежения с возмущением.

- среднее значение квадрата ошибки слежения без возмущения.

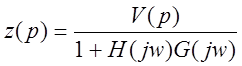
Уменьшение прироста  от возмущения  в асимптотически устойчивой линейной системе достигается за счет малости абсолютного значения функции чувствительности

 в полосе частот возмущения.

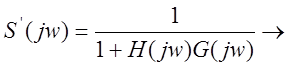 малое значение

 - большое значение, что противоречит условиям устойчивости.

Среднее значение квадрата входной переменной :

   

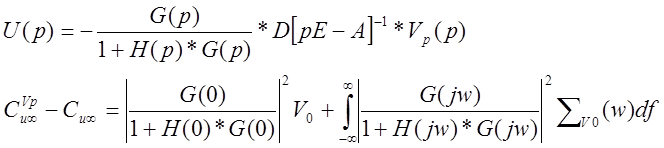
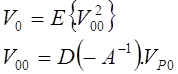
Чтобы получить малое увеличение  необходимо малое значение 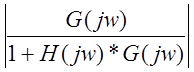 в диапазоне частот эквивалентного возмущения.

Влияние шума наблюдения на  и

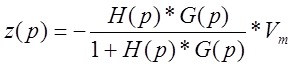
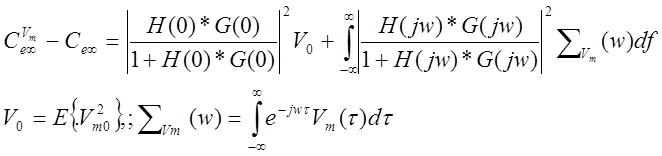
Чтобы уменьшить прирост установившегося среднего значения квадрата ошибки слежения от шума наблюдения в асимптотически устойчивой системе необходимо иметь малой величины 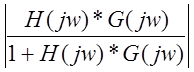 в полосе частот шума наблюдения.

Разностные уравнения и импульсные системы

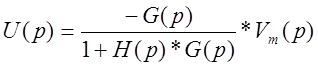
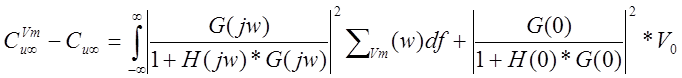
автоматического управления

Решетчатые функции:

               n – целое число

               Т – постоянная (период дискретности)

               

Введем время

Смещенная решетчатая функция.

При фиксированном

Смещенная решетчатая функция удовлетворяет условию: .

Если имеем разрыв первого рода в точке , то

         

В этом случае , т.е. .

функция двух аргументов.

Конечные разности решетчатых функций

 - конечная разность первого порядка

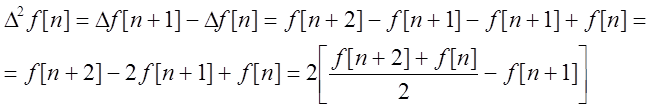
 - разность порядка .

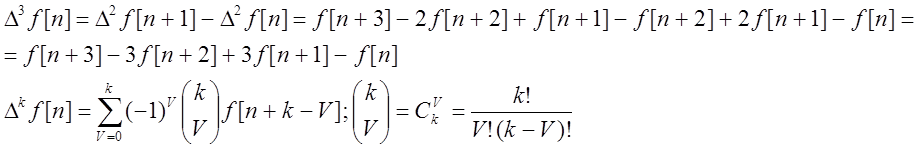
Примеры:

1.               

2.       

                             

3.             

                       

4.             

                         

                         

Линейность операции

Суммирование решетчатых функций

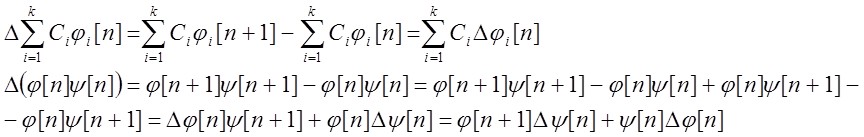
Пусть - решетчатая функция.

Найти  для которой  является первой разностью.

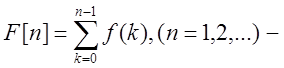первообразная функция.

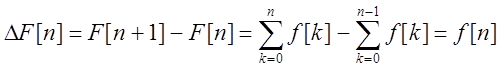
Если решетчатая функция определена при всех целочисленных значениях аргумента n=±0, ±1, ±2…, то 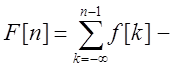ряд, который должен сходиться.

Если первообразная для , то  также является первообразной для  действительно .

Общий вид первообразной :.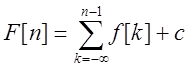

Значение c можно выразить через значение первообразной при каком-то фиксированном n=N, 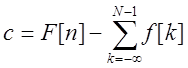 или .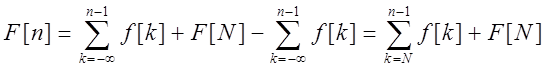

Если положить n=N+l : 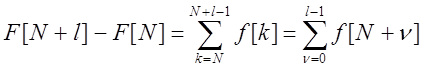   ,   l=[1,2,…]

или при N=0 :   .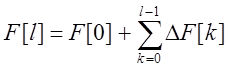

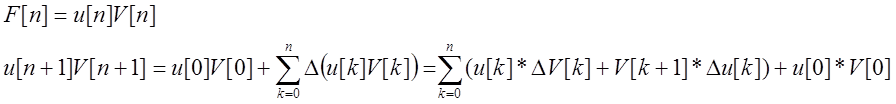
Для решетчатых функций справедлива формула 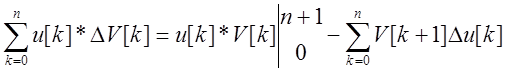суммирования по частям :

 - формула суммирования по частям

Пример:                  n=[0,1…]

;

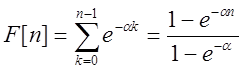Разностные уравнения.

Разностное уравнение связывает n-решетчатую функцию  и разности до некоторого порядка   или

Например:

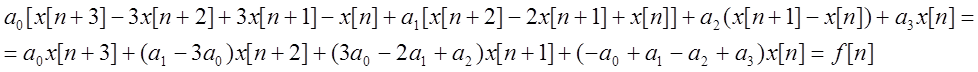
Если исходное уравнение содержит в явном виде  и , то исходное уравнение называется разностным порядка к.

Решетная функция , обращающая разностные уравнение в тождество называется его решением.