|
|||
 |
|||
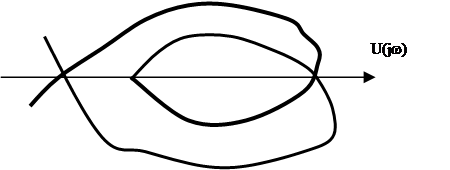
Пример: p3+p2+p+a0=0
a0=-p3-p2-p Þ a0=w2+jw(w2-1)
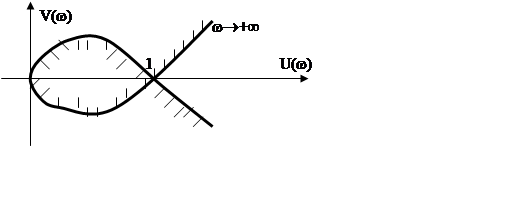 U(w)=w2 V(w)=w(w2-1) 0<a0<1
U(w)=w2 V(w)=w(w2-1) 0<a0<1
Анализ устойчивости одноконтурных динамических систем методом логарифмических АФЧХ.
![]()
 Анализ устойчивости
построен на критерии Найквиста-Михайлова.
Анализ устойчивости
построен на критерии Найквиста-Михайлова.
 |
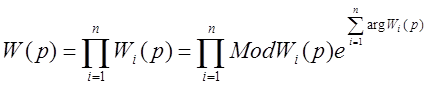
A(w)=20lg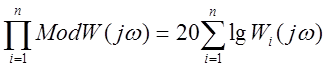
|
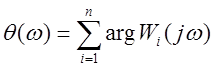
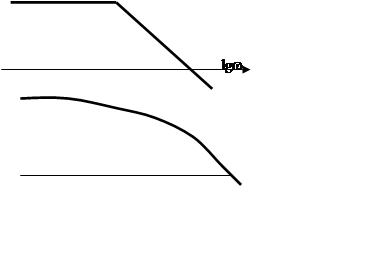
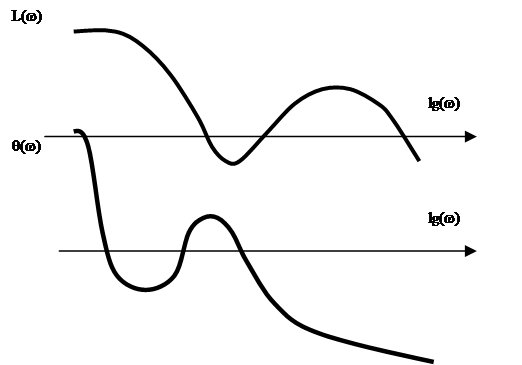
1).Для устойчивости замкнутой системы, у которой частотная характеристика разомкнутой системы первого рода, необходимо и достаточно, чтобы w1ср< w0cр.
![]() 2).
Для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы
разность между числом положительных и отрицательных переходов q(w)
через -p равнялась 0.
2).
Для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы
разность между числом положительных и отрицательных переходов q(w)
через -p равнялась 0.
 |
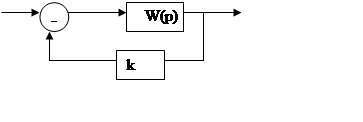
Метод корневого годографа.
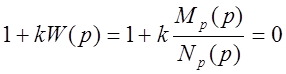
![]()
Совокупность точек рi, удовлетворяющих уравнению Np(p)+kMp(p)=0 при различных ki называют корневым годографом.
1) При к®0 полюсы замкнутой системы стремятся к полюсам разомкнутой системы.
2) При к®¥ полюсы замкнутой системы n стремятся к нулям m разомкнутой системы и (n-m) к бесконечности.
3) Число
асимптот (n-m) определят их
углы 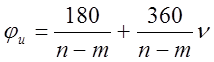 (1) n=(0.1…n-m-1). Все асимптоты пересекаются в
одной точке
(1) n=(0.1…n-m-1). Все асимптоты пересекаются в
одной точке 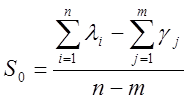 (2)
(2)
(1) следует из 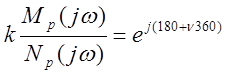
(2) 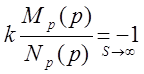
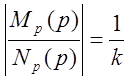
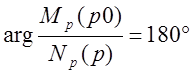
4) 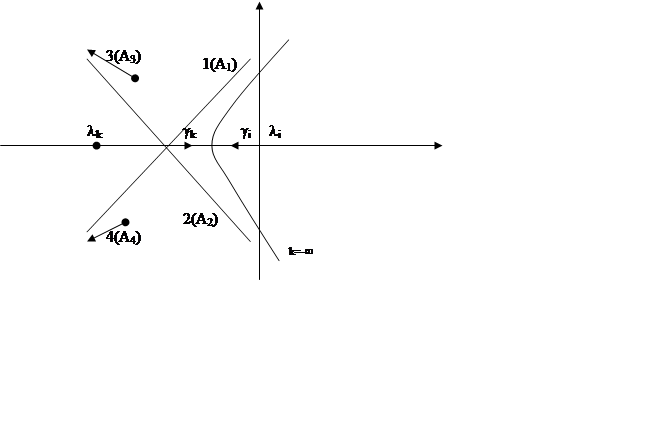 Участки годографа на оси абсцисс
определяются действительными нулями и полюсами.
Участки годографа на оси абсцисс
определяются действительными нулями и полюсами.
|
5) Точки отхода годографа от действительной оси определяются следующим образом:
(a,0) – координаты точки отхода
(a,e) – координаты корневого годографа, близкого к оси абсцисс
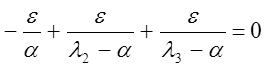
6) Точки пересечения годографа с мнимой осью определяются U(w)=0 V(w)=0, позволит определить w и к.
7) Углы
выхода годографа из комплексных полюсов и их подходы к комплексным нулям
определяются выражением: 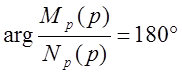 для
близкой точки.
для
близкой точки.
8) На корневом годографе различают параметр к. Корневой годограф – траектория движения корней в комплексной плоскости р, полученные с помощью уравнений замкнутой системы.
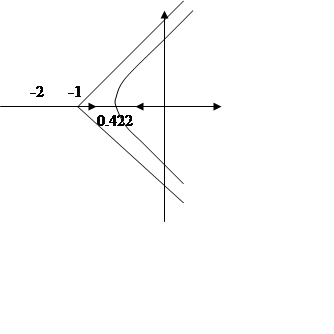 Пример:
Пример: 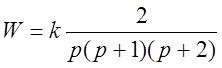
D(p)=p3+3p2+2p+2k, p1=0, p2=1, p3=-2
S0=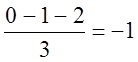
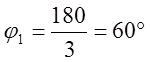
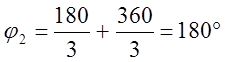
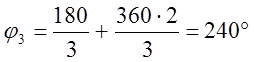
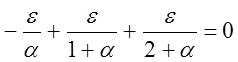
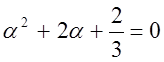 , a1=-0.422, a2=-1.58
, a1=-0.422, a2=-1.58
U(w)=-3w2+2k=0, w=![]()
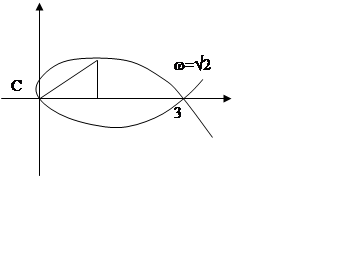 V(w)=j(2w-w3)=0, k=3
V(w)=j(2w-w3)=0, k=3
Метод Д-разбиения.
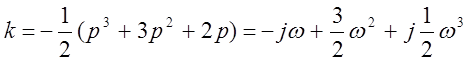
|
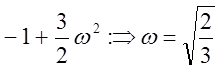
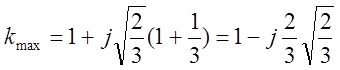
Анализ линейных САУ. Основные компоненты систем управления.
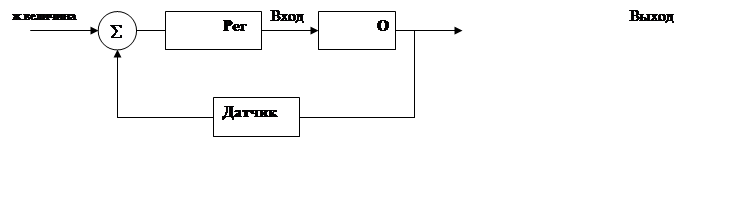 |
1. объект управления
2. датчик
3. регулятор
4. Задача управления или условие функционирования
Пример:
1)саморегулируемая система отопления дома.
2)спутниковая телевизионная антенна.
Общие формализованные черты:
1) Поведение – система дифференциальных уравнений или модель М.
2) Математический аппарат для анализа и синтеза получил название решающих процедур Т.
3) Исходные данные и ограничения А и С.
4) Проектное решение и его оценка R и K.
5) Обратная связь и возмущения.
6) Задание.
Задачи регулирования и слежения.
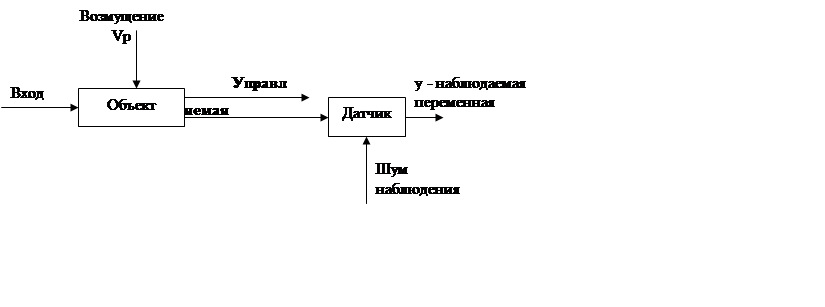 |
Переменные:
1) U(t)-управление
2) Vp(t)-возмущение
3) y(t)-наблюдение
4) Vm(t)-шум измерения
5) z(t)-управляемая величина
6) r(t)-задание или эталонная переменная
z(t)»r(t) t³t0-задача.
В исходных данных на проектирование необходимо учитывать:
1) неконтролируемость действующих на объект возмущений
2) недостоверность или переменность параметров объектов
3) неизвестность начального состояния
4) наблюдаемая переменная искажена шумом и не несет инфомации о регулируемой величине.
![]()
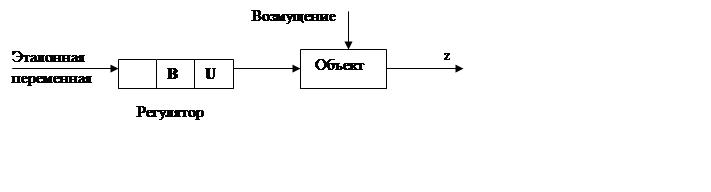
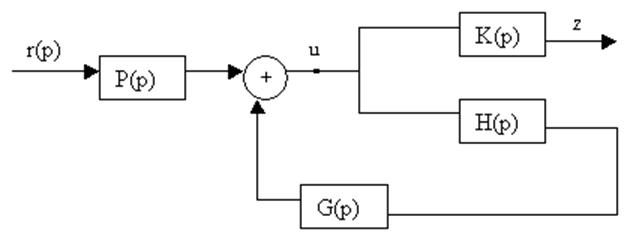
Разомкнутая система: управление основано только на прошлых и текущих значениях эталонной переменной.
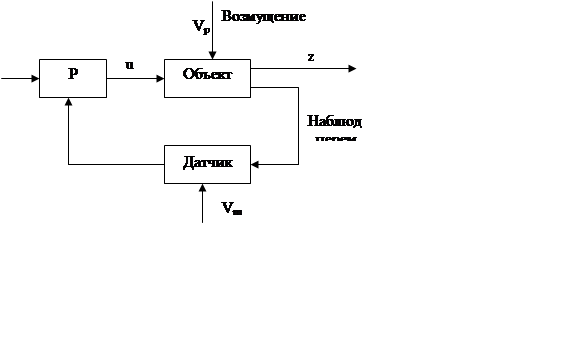
![]()
Пример системы управления.
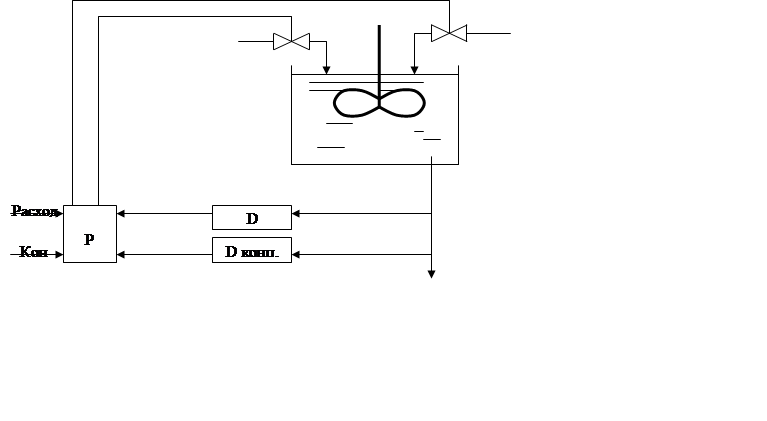 |
Замкнутые регуляторы могут накапливать информацию об объекте, его начальном состоянии уменьшать влияние возмущений и компенсировать неопределенность параметров.
Проектирование замкнутых систем.
Дифференциальные
уравнения объекта ![]()
![]() .
.
Наблюдаемая
переменная ![]() .
.
Управляемая
переменная ![]() .
.
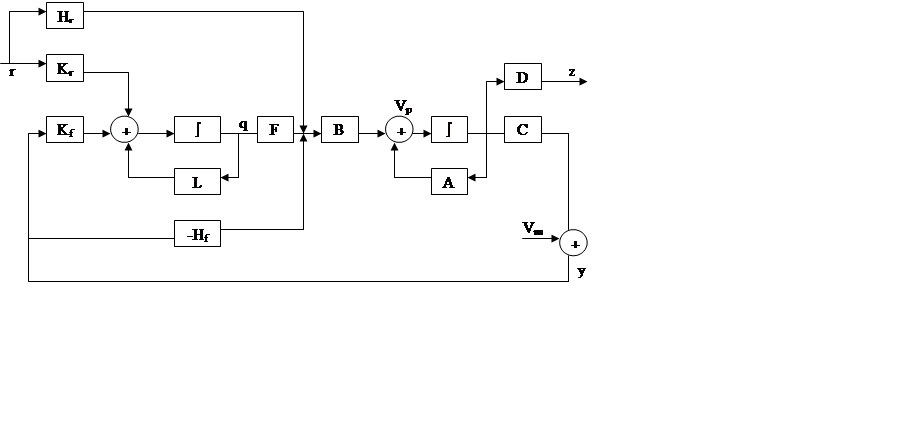 Дифференциальное уравнение регулятора
Дифференциальное уравнение регулятора
![]()
![]() .
.
Критерии качества работы:
Среднеее значение квадрата ошибки слежения Се(t) и среднее значение входной переменной Сu(t) определяется выражениями:
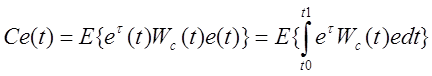
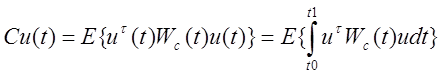
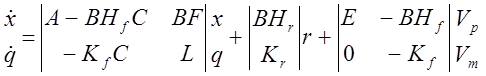
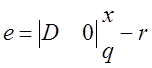
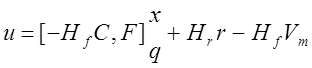
![]() и
и
![]() –
заданные неотрицательно определенные симметричные весовые матрицы в частном
случае диагональные.
–
заданные неотрицательно определенные симметричные весовые матрицы в частном
случае диагональные.
Основной принцип проектирования:
При проектировании следует добиваться минимума ![]() и
и ![]() .
.
1.Сначала вычисляют
![]() и
и ![]()
![]()
2.Затем вычисляют
![]()
![]()
3.![]()
![]()
Введем обозначения:
![]()
![]()
Подставим ![]() ,
где
,
где ![]() -постоянная
или средняя часть входного воздействия.
-постоянная
или средняя часть входного воздействия.
![]() -переменная
или вариабельная часть.
-переменная
или вариабельная часть.
![]()
![]()
![]()
![]()
![]()
![]()
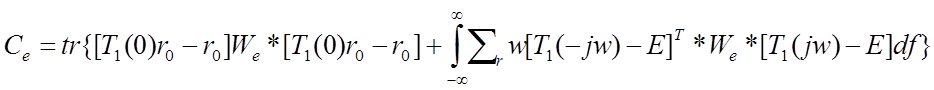
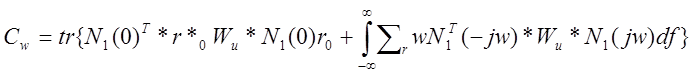
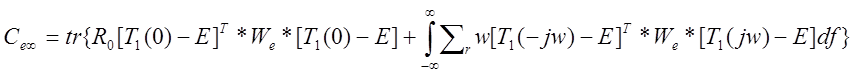
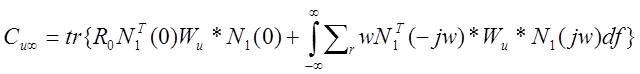
![]()
![]()
Матрица повариационных плотностей энергии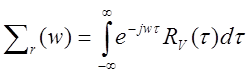
процесса ![]()
Например экспоненциального корректирования шума
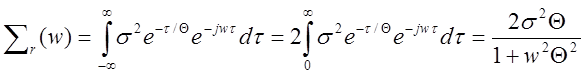
Квадратичные формы.
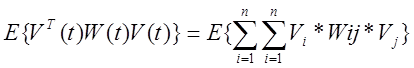
![]()
Допущения:
1. Система управления ассимптотически устойчива.
2.
Система управления имеет постоянные параметры и постоянные матрицы ![]() и
и ![]()
3.
![]() и
и
![]()
В случае многомерной векторной системы имеем:
![]()
![]()
![]()
Одномерная система управления
Входная величина и выходная (управляемая) переменная скалярные.
Принимаем ![]()
![]()
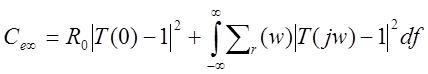
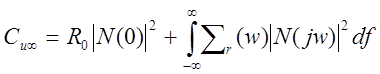
Для минимизации ![]() нужно придерживатьсь следующих
принципов.
нужно придерживатьсь следующих
принципов.
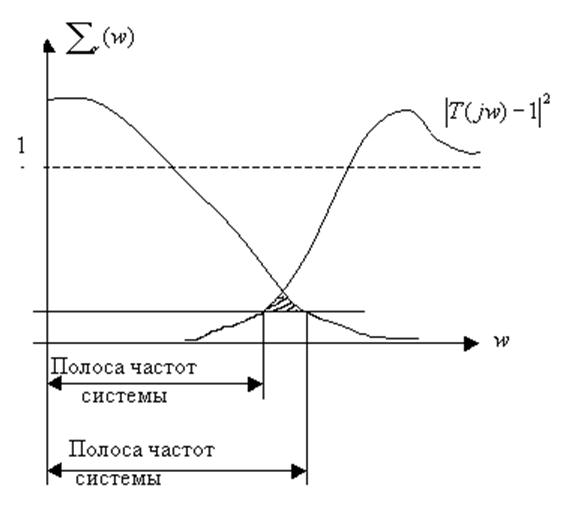 |
Общий подход: Разделить диапазон частот: там, где значительное ![]() нужно иметь
минимальное
нужно иметь
минимальное ![]() и
наоборот.
и
наоборот.
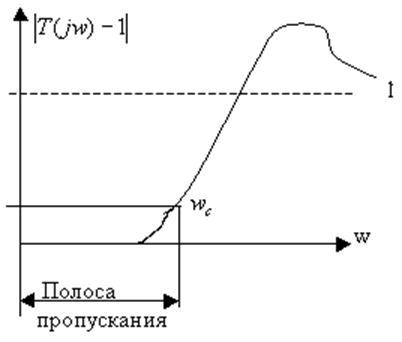 |
Полоса частот ![]() ,
где
,
где ![]() .
Полоса частот – интервал
.
Полоса частот – интервал ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.