Применение метода фазовых траекторий для синтеза оптимальных по быстродействию систем

Лекция №11

ПРИМЕНЕНИЕ МЕТОДА ФАЗОВЫХ ТРАЕКТОРИЙ ДЛЯ СИНТЕЗА ОПТИМАЛЬНЫХ ПО БЫСТРОДЕЙСТВИЮ СИСТЕМ

В задачах синтеза оптимальных по быстродействию систем, решаемых с помощью принципа максимума, дополнительно используют метод фазовых траекторий1'. При этом решение задачи сводится к определению уравнений линий или гиперповерхностей переключения, разделяющих фазовое пространство на области с различными траекториями движения изображающей точки. Так как фазовую плоскость или трехмерное фазовое пространство можно представить наглядно, то в простейших случаях для объектов, описываемых линейными дифференциальными уравнениями второго или третьего порядков, решение задачи синтеза оптимальных систем сводится к определению линий переключения на фазовой плоскости или поверхности переключения в трехмерном пространстве [2, 17].

Методика синтеза оптимальных по быстродействию замкнутых систем, основанная на применении метода фазовых траекторий, наиболее разработана для систем автоматической стабилизации выходной координаты объекта у(t)=x₁(t)=const, когда x_вх(t)=Х_вх × 1(t). При этом закон оптимального управления в соответствии с принципом максимума формируется в виде нелинейной зависимости координаты управления от координат вектора состояния [17, 18]:

.                        (3.138)

Сигнал управления меняет знак, если функция S(X), проходя нулевое значение, меняет знак, поэтому поверхность, определяемую равенством

S (X) = 0,                                    (3.139)

называют поверхностью переключения, а функцию S(X) – функцией переключения.

Знак сигнала управления на первом интервале определяется начальным X(t₀) и заданным X(Т) значениями вектора состояния:

.                         (3.140)

Аналитическое выражение функции переключения S(X) и релейный закон управления (3.138) определяют структуру оптимального по быстродействию регулятора.

В общем случае для автоматических систем программного управления и следящих систем задающее воздействие может иметь форму любого типового сигнала (линейного, квадратичного, гармонического и др.), т. е. х_вх(t)¹const. При этом структура регулятора, определяемая уравнением (3.138), не всегда будет обеспечивать оптимальное по быстродействию управление. Поэтому для систем программного управления и следящих систем, когда х_вх(t)=var, закон оптимального управления необходимо формировать в виде нелинейной зависимости координаты управления от ошибки Е(t), определяемой отклонением вектора состояния X(t) от вектора задающего воздействия Х_вх(t):

,                           (3.141)

где вектор ошибки Е = Х_вх – X. Функция переключения S(Е) в данном случае учитывает вектор задающего воздействия, поэтому поверхность переключения

S(Е) = 0                                      (3.142)

следует рассматривать в фазовом пространстве вектора ошибки

,

где .

Если корни характеристического уравнения объекта вещественные, то определение поверхностей переключения S(X) или S(Е) основано на справедливости теоремы «об n интервалах». При этом решение задачи выполним методом фазового пространства. При уравнениях высокого порядка целесообразно использовать каноническую форму

.                          (3.143)

Исключая из уравнений (3.143) время, получим систему уравнений, описывающих фазовые траектории в n-мерном фазовом пространстве. Для этого разделим все первые (n–1) уравнений на последнее и получим дифференциальные уравнения фазовых траекторий

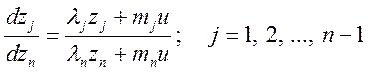.                  (3.144)

Проинтегрировав эти уравнения, найдем соответствующие зависимости между переменными состояния, характеризующими поверхность переключения [2, 11, 17], которая имеет (n–1)-ю размерность.

При определении аналитических выражений S(X) или S(Е) можно использовать известные методы построения фазовых траекторий и их аппроксимации [11, 12, 17]. Эта задача успешно решена для объектов второго и третьего порядков [2, 11, 12]. Для объектов более высокого порядка трудно получить практически реализуемые функции гиперповерхностей переключения, поэтому разработаны методы приближенного решения таких задач:

алгоритмический метод [2, 11] – основан на представлении решения уравнений состояния как линейного, так и нелинейного объекта, в виде степенных рядов для каждого интервала релейного управления и использует «попятное движение» от конечного состояния к начальному;

метод сечения пространства параметров – основан на выделении в системе канонических уравнений состояния нелинейного объекта независимой подсистемы уравнений первого или второго порядка и применении метода фазовой плоскости;

метод разделения движений – основан на расщеплении системы уравнений состояния как линейного, так и нелинейного объекта на подсистемы уравнений, характеризующих «быстрые» и «медленные» движения, и решении задачи сначала по уравнениям координат быстрых движений, а затем – медленных движений; при этом могут быть использованы как алгоритмический метод, так и методы построения фазовых траекторий, если уравнения расщепленных подсистем не превышают третий порядок.

При решении задачи синтеза оптимальных управлений методом фазовых траекторий могут быть учтены ограничения координат состояния и управления, а также контролируемые возмущения.