Надежность и диагностика технологических систем: Учебное пособие, страница 2

Рассмотрим и оценим влияние повреждения разных скоростных групп на выходной параметр Х (обычно точность обработки) и на показатели надежности.

1.1        Параметрические отказы.

          В теории надежности широко используются методы теории вероятности и статистики, поскольку надежность определяется случайным протеканием в объектах ТС различных явлений, вызывающих повреждение и отказы. Работоспособное состояние ТС характеризуется параметрами обработанной детали: точностью, шероховатостью, производительностью, стойкостью обработки и др. Выход параметра за пределы, установленные технической документации (ТД), означает отказ. Время выхода параметра на предельный уровень имеет случайный характер. Наработка на отказ и другие нерегламентированные временные показатели являются случайными величинами, прогнозируемыми методами теории вероятности. Их точное значение определяется при диагностировании ТС.

Наработка на отказ Т определяется законом ее распределения. Законом распределения Т является соотношение, устанавливающее связь между значениями Т и соответствующими им вероятностями. Закон распределения часто задают в виде функции распределения наработки до отказа Т, определяющей вероятностью Р того, что Т не превысит некоторого Т_i, т.е. по времени  -¥ ≤Т≤Т_i.

Таблица 1.1.

               F(T)=P(T≤T_i)                       (1.1)

Функцию F(T) называют интегральным законом распределения. Статическая вероятность отказа за время Т_i определяется как отношение числа отказов n (Т_i) с наработкой до отказа менее Т_i и общему числу отказов N:

               F(Т_i)= n(Т_i)/N             (1.2)

Основным показателем безотказности технологической системы является безотказность работы Р(Т), т.е. вероятность того, что наработка до отказа Т не будет ниже заданного Т_i:

                Р(Т_i)=1-n(Т_i)/N                   (1.3)

Вероятность отказа F(Т_i)=1-P(Т_i)

Вероятность безотказной работы в течении времени Т_i можно найти через плотность распределения величины- производную функции распределения F(T), т.е. F^(T)=f(T). Функция f(T) характеризует плотность, с которой распределяется значением случайной величины (наработки на отказ ТС). Запишем:

F(T)=∫^Ti_-∞f(T)dT              (1.4)

Тогда вероятность безотказной работы ТС в течении Т_i будет равна площади под кривой f(T) на участке от Т_i до +∞ и рассчитывается по формуле:

P(Т_i)=1-∫^Ti_-∞f(T)dT                    (1.5)

Плотность распределения получают в результате статических исследований.

Для анализа причин отказов определяют интенсивность отказов λ(Т), т.е. вероятность отказа в единицу ΔТ после времени Т при условии, что до этого отказов не было.

         l(Т)= f(T)/P(T)                 (1.6)

Статистическая интенсивность отказов определяется:

l(Т)=n(ΔT)/(N_cp(ΔT)*ΔT)           (1.7)

Где: n(ΔT)/ΔT- число отказов в единицу времени.

N_cp(ΔT)=(N(T)+N(T+ΔT))/2 – среднее число случаев безотказной работы в начале и в конце интервала. Зависимость интенсивности отказов от времени может иметь три зоны (рис.1.1).

           В зоне I высокая уменьшающаяся со временем интенсивность определяется дефектами изготовления объектов происходит отбор ненадежных объектов. Это зона приработки. В зоне III повышение интенсивности отказов определяется повреждениями, приобретенными при эксплуатации за длительный период времени.

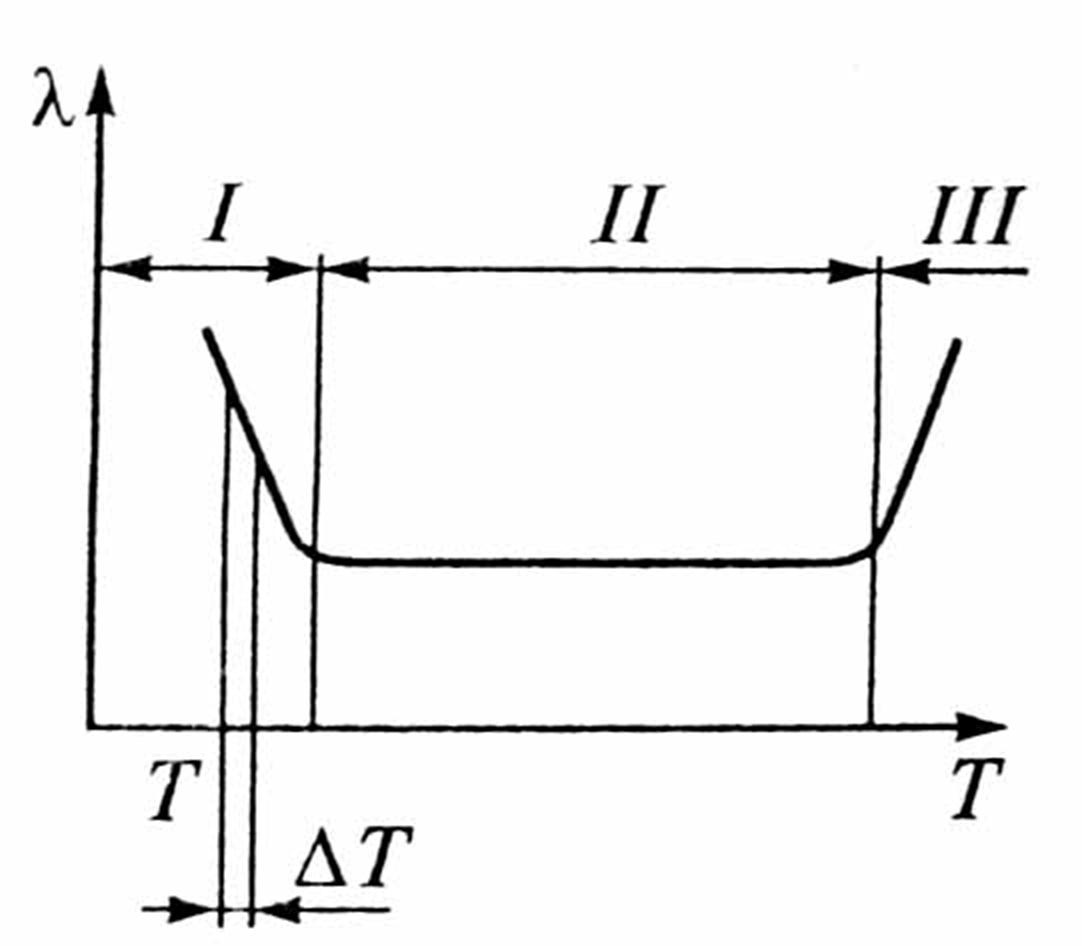
Рис. 1.1 Зависимость интенсивности отказов от времени.

В зоне II производится работа ТС, где интенсивность отказов стабильны и отказы носят случайный характер.

В задачах надежности часто используется нормальное распределение случайных величин:

F(T)=1/(s_T√2p)e^-(T-mT)2/2s_T²       (1.8)

Где:

mT- математическое ожидание наработки до отказа;

s_T- среднее квадратичное отклонение наработки до отказа.

Нормальное распределение используется также для приближенных расчетов в тех случаях, когда имеет место биноминальное распределение или распределение Пуассона.

Функция распределения F(T) имеет вид:

F(T)=∫^T_-∞f(T)dT=1/s_T √2π ∫_-∞^Tl^-(T-mT)2/2s_T²dT           (1.9)

 

Интеграл не выражается через элементарные функции и для его вычисления пользуются таблицами функций Лапласа или интеграла вероятностей

Ф(X)=2/√π∫^x₀ e^-x2dx

Использование функции Лапласа не всегда удобно и наработку на отказ определяют по наиболее простым формулам:

T_γ=mT-u_γs_T

Где T_γ – время безотказной работы с вероятностью γ;

u_γ- квантиль нормального распределения;

γ- вероятность безотказной работы.

γ=Р(Т) и может быть выражено в %. Тогда величину Т_γ называют гамма-процентной наработкой. Значение γ во избежание тяжелых последствий при отказе берут высоким (обычно γ=0,95). При γ=0,95  квантиль u_γ=1,645.

Нормальный закон только приближенно описывает распределение наработки до отказа сложных систем. Функция f(T) в отличие от нормального закона получается несимметричной. Для определения показателя надежности экспериментально получают гистограмму, для которой далее подбирают теоретическую кривую f(T) наработки до отказа.

Эффективная технологическая система должна быть высоконадежной и иметь значительную наработку на отказ, что требует значительного времени для определения f(T). Для случаев функциональных отказов используют ускоренные испытания на форсированных режимах. При оценке параметрической надежности ускоренные испытания недопустимы, поскольку форсированные режимы изменяют протекание процессов, приводящих к отказам.

Параметрические отказы являются как результатом комплексного воздействия различных элементов и узлов ТС, так и вызываются одним из них. Наработка на отказ инструментов значительно меньше, чем  у других элементов ТС, поэтому и надежность их значительно ниже.

1.3 Виды повреждения.

В каждый момент времени работы ТС значение выходного параметра Х является результатом воздействия суммы повреждения всех скоростных групп, воздействия которых независимы друг от друга.

X_max=X(U₁)+X(U₂)+X(U₃)                  (1.10)

Где:

 U₁ , U₂ ,U₃- быстропротекающие, средне- и медленнопротекающие процессы;