Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 9

Доказательство. Рассмотрим тело с центром масс в точке М (рис. 5). Требуется определить его момент инерции относительно оси х-х. Проведем ось y-y, параллельную оси х-х и отстоящую от нее на расстоянии L. Пусть расстояние от произвольной i-й точки тела до оси х-х - , a от той же точки до оси y-y -  ( может быть и положительным, и отрицательным в зависимости от положения i–й точки относительно оси y-y). Тогда  и, следовательно,

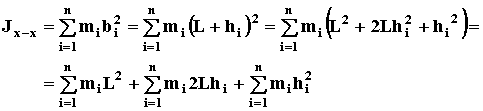
Вынеся из-под знака суммирования постоянные величины и учитывая, что

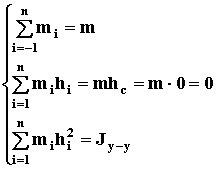                                                    получим

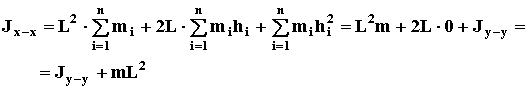
ч.т.д.                                    (49)

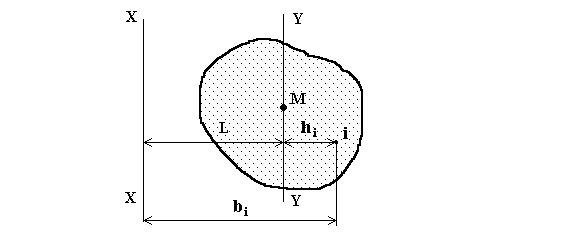
Рис. 5.

Основываясь на полученном результате, можем сделать вывод, что, поскольку величина всегда положительна, то СОБСТВЕННЫЙ МОМЕНТ ИНЕРЦИИ ЯВЛЯЕТСЯ МИНИМАЛЬНО ВОЗМОЖНЫМ МОМЕНТОМ ИНЕРЦИИ ДАННОГО ТЕЛА ПРИ СОХРАНЕНИИ НАПРАВЛЕНИЯ ОСИ ВРАЩЕНИЯ.

Кроме того, поскольку мы рассматриваем только абсолютно жесткие тела, то ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ ЕСТЬ ВЕЛИЧИНА ПОСТОЯННАЯ.

МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ

СИСТЕМЫ

МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ (КИНЕТИЧЕСКИЙ МОМЕНТ) относительно выбранной точки пространства – это результат векторного произведения вектора, проведенного из выбранной точки в любую точку линии действия силы на вектор количества движения материальной точки

                                                   (51)

МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ (КИНЕТИЧЕСКИЙ МОМЕНТ СИСТЕМЫ) относительно выбранной точки пространства – это сумма моментов количества движения всех материальных точек системы относительно той же точки

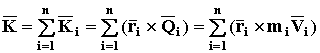
Ограничимся рассмотрением только плоских задач. В этом случае аналогично моменту силы (СТАТИКА стр. 9) можно считать, что момент количества движения точки является скалярной величиной и равен

где v_i – модуль вектора скорости точки;

h_i –плечо.

Знак момента количества движения выбирается так же, как и знак момента силы (СТАТИКА стр. 7).

ТЕОРЕМА Д10. Момент количества движения поступательно движущегося тела (кинетический момент поступательного движения) равен произведению массы тела на скорость любой точки тела и на плечо скорости центра масс относительно выбранной точки.

Доказательство. Как известно (КИНЕМАТИКА стр. 8), при поступательном движении тела скорости всех точек тела равны , тогда, пользуясь коммутативным свойством суммирования, разбив тело на материальные точки, получим

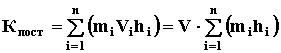
То, что получено в скобках, может быть выражено через координату центра масс системы (СТАТИКА стр. 15)

 

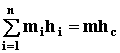
где h_c – плечо скорости центра масс системы относительно выбранной точки.

Тогда

                                                   (51)

ТЕОРЕМА Д11. Момент количества движения вращательно движущегося тела (кинетический момент вращательного движения) равен произведению момента инерции тела относительно оси вращения на угловую скорость.

Доказательство. Как известно (КИНЕМАТИКА стр. 9), при вращательном движении тела скорости всех точек тела могут быть выражены

где  угловая скорость тела,

расстояние от рассматриваемой точки до оси вращения.

Тогда, пользуясь коммутативностью суммирования, разбив тело на материальные точки и учитывая определение момента инерции (48), получим

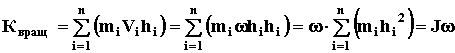      (52)

ТЕОРЕМА Д12. Момент количества движения плоскопараллельно движущегося тела (кинетический момент плоскопараллельного движения) равен сумме момента количества движения центра масс тела относительно выбранной точки и произведения собственного момента инерции тела на угловую скорость

                                                   (53)

Доказательство. Без доказательства.

ЭЛЕМЕНТАРНЫЙ МОМЕНТНЫЙ ИМПУЛЬС – это произведение момента силы на элементарный промежуток времени действия силы

Полный МОМЕНТНЫЙ ИМПУЛЬС – это сумма всех элементарных моментных импульсов за время действия силы

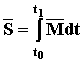                                                                      (54)