Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 3

Выражение (11) представляет собой неявную зависимость скорости от времени. Далее после интегрирования следует из полученного выражения выразить скорость и еще раз проинтегрировать.

г) Сила зависит от координат

Тогда имеем из (3)

                                                                      (12)

Уравнение интегрировать пока нельзя, так как в нем не разделены переменные. Сделаем замену переменных как в предыдущем разделе и, кроме того, учтем, что

                                  (13)

Подставив все это в выражение (12), получим

Разделим переменные

Теперь, проинтегрировав, получим

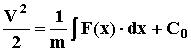                                                  (14)

Полученное выражение представляет собой неявную зависимость скорости точки от ее координат. Если далее вернуться к переменной х и разделить переменные, получим

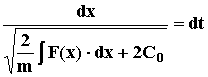
Проинтегрировав еще раз, получим

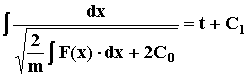                                         (15)

где С₁ – константа интегрирования.

Уравнение (15) в неявном виде описывает зависимость координат точки от времени.

При решении обратной задачи динамики материальной точки необходимо обращать внимание на характер действующих сил и в связи с этим выбирать соответствующий путь решения задачи. Кроме того, необходимо учитывать, что именно требуется определить по условию задачи. Например, если в задаче требуется определить зависимость скорости от перемещения или положение точки, когда ее скорость будет иметь определенное значение, то независимо от действующих сил рационально будет использовать уравнение (14).

УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ В ЕСТЕСТВЕННОЙ СИСТЕМЕ КООРДИНАТ

Если уравнение (1) разложить по осям естественной системы координат (КИНЕМАТИКА стр. 4), получим

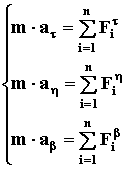
Учитывая особенности разложения вектора ускорений в естественной системе координат (КИНЕМАТИКА стр.5), получим

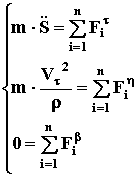                                                           (16)

где S – закон движения в естественной системе координат (КИНЕМАТИКА стр. 4).

Отметим, что чисто технически решать систему уравнений (16) в два раза проще, чем уравнения (2), потому что только первое из уравнений (16) является дифференциальным второго порядка, второе имеет только первый порядок, а третье вообще не дифференциальное. Однако пользоваться уравнениями (16) можно только в том случае, если заранее известна траектория движения.

УРАВНЕНИЯ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ

МАТЕРИАЛЬНОЙ ТОЧКИ

При сложном движении материальной точки (КИНЕМАТИКА стр. 16), согласно теореме К3 (Кориолиса)

Тогда из (1) получаем

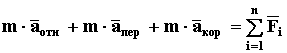
или 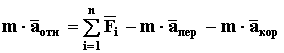                                        (17)

При определении характеристик движения материальной точки в подвижной системе координат необходимо при составлении дифференциальных уравнений движения учитывать движение самой системы координат. Уравнение (17) существенно раздвигает рамки классической механики и позволяет решать задачи в неинерциальных системах координат. Уравнение (17) называют УРАВНЕНИЕМ ДВИЖЕНИЯ материальной точки В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ.

КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ

а) Движение под действием восстанавливающей силы

ВОССТАНАВЛИВАЮЩАЯ СИЛА –это сила, которая прямо пропорциональна смещению от некоторой точки пространства и направленная всегда к этой точке

, где с=const – коэффициент пропорциональности;

х₀ – координата точки пространства, к которой направлена восстанавливающая сила.

Пусть на материальную точку действует только восстанавливающая сила. Этот случай движения является одной из разновидностей движения материальной точки под действием силы, зависящей от координат, однако в этом случае уравнение (15) интегрируется и решение можно получить аналитически. Разберем подробнее.

Для простоты будем считать, что х₀=0, тогда уравнение (3) примет вид

                                                                 (18)

Разделим полученное уравнение на m и введем обозначение

                                                                        (19)