Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 7

Движение механической системы в отсутствие внешних сил

Теорема Д4. Если внешние силы, действующие на механическую систему, уравновешены в некотором направлении, то центр масс системы в этом направлении будет двигаться с постоянной скоростью.

Доказательство. Выберем систему координат таким образом, чтобы ось Х совпадала с направлением, в котором внешние силы уравновешены, т.е. сумма проекций внешних сил на ось Х равна нулю

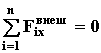
Тогда, согласно теореме Д3

Так как , следовательно

Если проинтегрировать последнее выражение, то получим

,   ч.т.д.

ТЕОРЕМА Д5. Если внешние силы, действующие на механическую систему, уравновешены в некотором направлении и в начальный момент система покоилась, то центр масс системы остается неподвижен все время движения.

Доказательство. Повторив рассуждения, приведенные в доказательстве предыдущей теоремы, получим, что скорость центра масс должна остаться такой же, какой она была в начальный момент, т.е. нулевой

Проинтегрировав это выражение, получим

,   ч.т.д.

ТЕОРЕМА Д6. Если внешние силы, действующие на механическую систему, уравновешены в некотором направлении и в начальный момент система покоилась, то сумма произведений масс каждого из тел системы на абсолютное смещение его собственного центра масс в том же направлении равна нулю.

Доказательство. Выберем систему координат таким образом, чтобы ось Х совпадала с направлением, в котором внешние силы уравновешены или отсутствуют (F₁, F₂, …, F_k на рис. 3), т.е. сумма проекций внешних сил на ось Х равна нулю

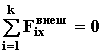
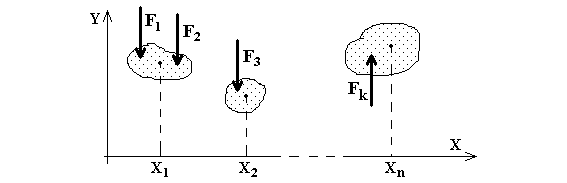
Рис. 3.

Пусть система включает n тел и координаты центров масс каждого тела равны . Тогда в начальный момент движения должно быть справедливо выражение (СТАТИКА стр. 15)

.

По прошествии некоторого промежутка времени Dt, тела системы переместились в новое положение (рис. 4)

где  абсолютное смещение j-го тела за рассматриваемое время.

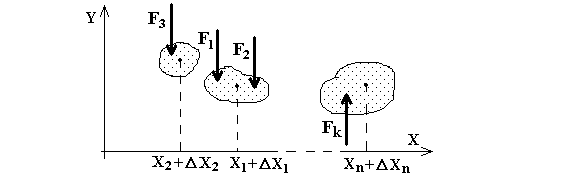
Рис. 4.

Для нового положения центра масс можем снова написать выражение

На основании теоремы Д5 можем сделать вывод, что центр масс системы по оси Х не смещается, т.е.  или

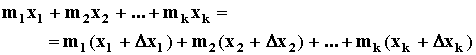
Раскрыв скобки и приведя подобные, получим

,   ч.т.д.                       (42)

Уравнения поступательного движения тела

Поскольку при поступательном движении ускорения всех точек тела одинаковы (КИНЕМАТИКА стр. 8), то уравнение движение будет как в формуле (41), только вместо ускорения центра масс можно использовать ускорение любой точки тела. Если спроектировать это уравнение на оси координат, получим

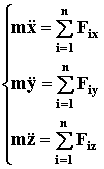                                                                 (43)

КОЛИЧЕСТВО ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ

КОЛИЧЕСТВО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ – это произведение массы точки на ее скорость

КОЛИЧЕСТВО ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ – это сумма количеств движения всех точек системы

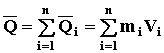                                                       (44)

При использовании формулы (44) не обязательно разбивать систему только на материальные точки: можно на отдельные тела или группы тел, но внутри этих групп не должно быть относительных смещений.

ТЕОРЕМА Д7. Количество движения системы материальных тел равно произведению массы всей системы на скорость ее центра масс.

Доказательство. Воспользовавшись определением скорости (КИНЕМАТИКА стр. 3), понятием центра масс (СТАТИКА стр. 15) и коммутативностью операций суммирования и дифференцирования, выполним преобразования

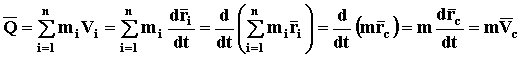
ч.т.д.               (45)

Следствие. Количество движения тела равно произведению его массы на скорость его центра масс.

Термин ЭЛЕМЕНТАРНЫЙ в сочетании с какой-либо характеристикой означает дифференциал этой характеристики.

Термин СУММА ЭЛЕМЕНТАРНЫХ в сочетании с какой-либо характеристикой означает интеграл этой характеристики.

ЭЛЕМЕНТАРНЫЙ ИМПУЛЬС СИЛЫ – это произведение силы на элементарный промежуток времени действия силы

                                                                    (46)