Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 10

Постоянный момент силы

Если то

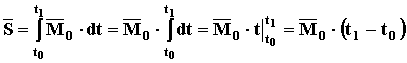
МОМЕНТНЫЙ ИМПУЛЬС ПОСТОЯННОГО МОМЕНТА СИЛЫ РАВЕН ПРОИЗВЕДЕНИЮ МОМЕНТА СИЛЫ НА ПРОМЕЖУТОК ВРЕМЕНИ ДЕЙСТВИЯ СИЛЫ.

ТЕОРЕМА Д13. (вторая основная теорема динамики). Изменение момента количества движения механической системы равно сумме моментных импульсов всех внешних сил, действующих на систему.

Доказательство. Рассмотрим произвольную механическую систему. Она состоит из конечного числа материальных тел. На основании аксиомы Д2 разобьем каждое тело системы на материальные точки. Пусть всего получено n таких точек. Для каждой такой точки можем составить уравнение (51). Продифференцируем это выражение, учитывая свойство дифференциала и определение скорости и ускорения (КИНЕМАТИКА стр. 3)  получим

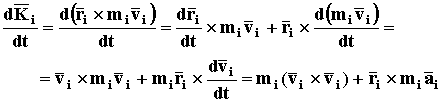
По свойствам векторного произведения произведение вектора самого на себя всегда равно нулю. Кроме того, согласно аксиомы Д4 и определения момента силы (СТАТИКА стр. 7)

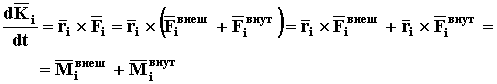
Просуммируем полученное выражение для всех точек системы

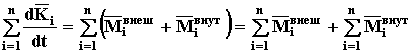
По свойству внутренних сил (теорема Д2) последнее слагаемое всегда равно нулю. Используя также свойства суммирования и дифференцирования, получим

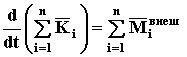
Согласно определению (52) окончательно будет

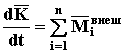                                                             (55а)

Если проинтегрировать это выражение, получим с учетом определения (54)

                                                             (55б)

Верхнее выражение называют дифференциальной формой теоремы, а нижнее – интегральной. На практике можно пользоваться любой из этих формулировок в зависимости оттого, что дано по условию задачи и что требуется определить (для определения ускорений удобнее пользоваться формулой (55а), для скоростей – (55б)).

Движение под действием центральной силы

ЦЕНТРАЛЬНАЯ СИЛА – это сила, линия действия которой проходит через одну и ту же неподвижную точку в выбранной системе координат.

Рассмотрим движение точки М, на которую действует центральная сила  направленная всё время в точку O (рис. 4). Поскольку линия действия силы пересекает точку O , то момент силы  относительно точки O всегда равен нулю и согласно теореме Д13

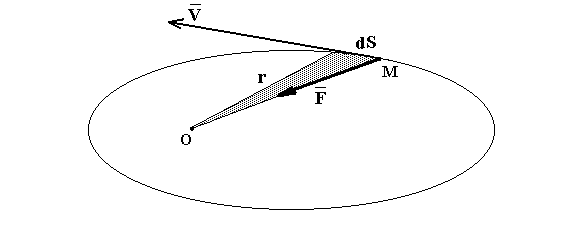
Рис. 6.

Если траектория – плоская кривая, то

Пусть . Поскольку модуль скорости  пропорционален длине элементарной дуги траектории dS, то можно считать, что  = const. С небольшой степенью погрешности можно считать, что площадь заштрихованного на рис. 6 треугольника

Величина s называется СЕКТОРИАЛЬНОЙ ПЛОЩАДЬЮ.

МАТЕРИАЛЬНАЯ ТОЧКА ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ ДВИЖЕТСЯ ТАКИМ ОБРАЗОМ, ЧТО СЕКТОРИАЛЬНАЯ ПЛОЩАДЬ, ОПИСЫВАЕМАЯ ЕЮ ЗА РАВНЫЕ ПРОМЕЖУТКИ ВРЕМЕНИ, БУДЕТ ОДИНАКОВА. Получается, что вблизи от точки O материальная точка будет двигаться с относительно большой скоростью, а вдали – с маленькой. Это действительно наблюдается при движении космических объектов по вытянутым эллиптическим орбитам.

Уравнение вращательного движения тела

Если рассматривается вращательное движение одного тела, то, подставив (52) в (55а), получим

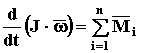
Так как J = const, то

Поскольку производная от угловой скорости – это угловое ускорение (КИНЕМАТИКА стр.9), то окончательно имеем

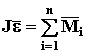                                                                    (56)

Уравнения плоскопараллельного движения тела

Как известно из кинематики (КИНЕМАТИКА стр. 11), плоскопараллельное движение можно представлять как выполнение телом одновременно и поступательного и вращательного движения. Поэтому уравнения движения для этого случая должны включать уравнения аналогичные и (43), и (56). Проще всего уравнения получаются, если в качестве полюса выбирать центр масс тела. Кроме того, выберем систему координат таким образом, что оси X и Y лежали в плоскости движения, а ось Z перпендикулярна ей. Тогда уравнения движения могут быть выражены в проекциях в следующем виде

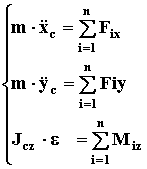                                                               (57)

где x_c и y_c - координаты центра масс тела;

J_cz - собственный момент инерции тела относительно оси, перпендикулярной плоскости движения.