Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 12

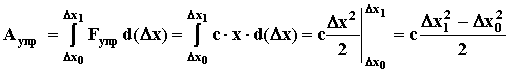
(65)

где Dх₀ – начальное относительное смещение;

Dx₁ – конечное относительное смещение.

РАБОТА УПРУГОЙ СИЛЫ РАВНА ПРОИЗВЕДЕНИЮ ПОЛОВИНЫ ЖЕСТКОСТИ ТЕЛА НА РАЗНОСТЬ КВАДРАТОВ КОНЕЧНОГО И НАЧАЛЬНОГО СМЕЩЕНИЯ.

Работа силы, приложенной к вращательному телу

Допустим некоторое тело вращается вокруг оси z-z под действием силы  (рис. 7). Спроектируем эту силу на любую плоскость, перпендикулярную оси вращения, получим проекцию F_t. Поскольку точка приложения силы может двигаться только по дуге окружности, то её элементарное перемещение можно принять равным dS, где S – длина дуги траектории. Тогда

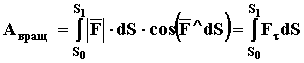
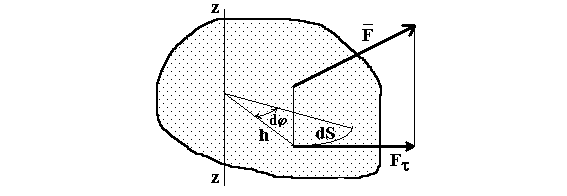
Рис. 7.

Как известно из геометрии длина дуги окружности равна произведению радиуса на центральный угол, тогда  Кроме того, произведение силы на плечо равняется моменту силы, поэтому

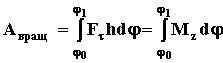                                             (66)

Если момент силы постоянен, то

РАБОТА СИЛЫ, СОЗДАЮЩЕЙ ПОСТОЯННЫЙ МОМЕНТ ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ ТЕЛА, РАВНА ПРОИЗВЕДЕНИЮ ЭТОГО МОМЕНТА НА УГОЛ ПОВОРОТА ОТ НАЧАЛЬНОГО ДО КОНЕЧНОГО ПОЛОЖЕНИЯ ТЕЛА.

Работа силы трения скольжения

Если тело совершает поступательное перемещение, то работа определяется по формуле (65).

Если тело вращается, а сила трения приложена не на оси вращения, то по формуле (68).

Если тело катится без проскальзывания, то работа силы трения равна нулю, поскольку мгновенный центр скоростей будет находиться в этом случае в точке приложения силы трения, т.е. эта точка в любой момент времени будет мгновенно неподвижна и, следовательно, работа не совершается.

ТЕОРЕМА Д15(третья основная теорема динамики). Изменение кинетической энергии механической системы равняется сумме работ всех сил, действующих на эту систему.

Доказательство. Рассмотрим произвольную механическую систему. Она состоит из конечного числа материальных тел. На основании аксиомы Д2 разобьем каждое тело системы на материальные точки. Пусть всего получено n таких точек. Для каждой i-ой точки, сделав замену (13), можем написать уравнение движения в виде

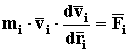
Воспользовавшись известной формулой дифференцирования , внеся под знак дифференцирования как константу массу точки и перебросив знаменатель из левой части в правую, получим

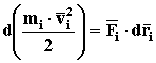
С учетом сделанных определений (58) и (62) можем записать

Просуммируем полученное выражение по всем точкам механической системы, получим

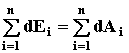
Воспользовавшись свойствами суммирования и дифференцирования, согласно определения кинетической энергии системы

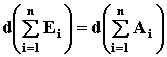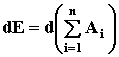 или                           (67а)

Проинтегрировав это выражение, получим

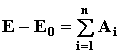                                                              (67б)

Выражение (67а) называют дифференциальной формой теоремы, а (67б) – интегральной. На практике можно пользоваться любой из этих формулировок в зависимости от того, что дано по условию задачи и что требуется определить.

Неизменяемая механическая система

МЕХАНИЧЕСКАЯ СИСТЕМА называется НЕИЗМЕНЯЕМОЙ, если относительные смещения тел, входящих в систему, отсутствуют.

Поскольку относительные смещения внутри системы отсутствуют, то тогда отсутствует работа внутренних сил и теорема Д15 формулируется следующим образом.

Следствие 1. Изменение кинетической энергии неизменяемой механической системы равняется сумме работ всех внешних сил, приложенных к системе

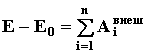                                                         (68)

Система с идеальными связями

ВОЗМОЖНОЕ ПЕРЕМЕЩЕНИЕ – это любое бесконечно малое перемещение произвольной точки тела, которое допускают наложенные на тело связи без изменения самой связи.

ИДЕАЛЬНАЯ СВЯЗЬ – это связь, у которой сумма возможных работ всех её реакций на всех возможных перемещениях системы равна нулю.

Все связи, которые рассматривались до этого (СТАТИКА стр. 3-6), исключая шероховатую поверхность, являются идеальными.

АКТИВНАЯ СИЛА – любая сила, действующая в системе, исключая силы реакции.

Из определения идеальных связей непосредственно следует, что работа реактивных сил в случае системы с идеальными связями всегда равна нулю.