Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 4

Тогда уравнение (18) примет вид

                                                                   (20)

Характеристическое уравнение, соответствующее полученному дифференциальному уравнению, имеет вид

Корнями такого алгебраического уравнения являются мнимые числа

где j – мнимая единица.

В этом случае решение уравнения (20) ищется в виде

                                               (21)

где С₁ и С₂ – константы интегрирования.

ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ – это такое движение материальной точки, когда закон ее движения изменяется пропорционально синусу, аргумент которого в свою очередь прямо пропорционален времени движения.

АМПЛИТУДА колебаний – это коэффициент перед синусом в законе гармонического движения.

ФАЗА колебаний – это аргумент синуса в законе гармонического движения.

ПЕРИОД колебаний – это промежуток времени, по истечении которого фаза колебаний повторяется.

КРУГОВАЯ ЧАСТОТА колебаний – это количество повторений фазы колебаний за одну секунду.

Из тригонометрии известно, что выражение (21) можно преобразовать к виду

                                                          (22)

где А и a - постоянные величины.

С учетом введенных определений можно сделать вывод, что ДВИЖЕНИЕ ТОЧКИ ПОД ДЕЙСТВИЕМ ВОССТАНАВЛИВАЮЩЕЙ СИЛЫ ЯВЛЯЕТСЯ ГАРМОНИЧЕСКИМ КОЛЕБАНИЕМ, причем в выражении (22) А – это амплитуда; a - начальная фаза колебаний; kt+a - текущая фаза колебаний; k – круговая частота.

Период колебаний можно определить по формуле

Продифференцировав выражение (22), получим зависимость скорости колебаний от времени

                                                            (23)

Примем начальные условия

                                                         (24)

Подставив (24) в (22) и (23), получим систему двух уравнений с двумя неизвестными А и a

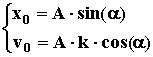
Выполнив несложные преобразования, можем получить выражение для амплитуды и начальной фазы колебаний (полученные формулы верны только при наличии одной восстанавливающей силы; при наличии других сил выражения изменятся)

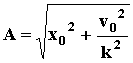
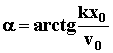
Полученные результаты позволяют сделать вывод, что КРУГОВАЯ ЧАСТОТА и ПЕРИОД КОЛЕБАНИЙ НЕ ЗАВИСЯТ ОТ НАЧАЛЬНЫХ УСЛОВИЙ, а определяются только жесткостью и инерционностью колебательной системы. В свою очередь АМПЛИТУДА и НАЧАЛЬНАЯ ФАЗА КОЛЕБАНИЙ ЗАВИСЯТ ЕЩЕ И ОТ НАЧАЛЬНЫХ УСЛОВИЙ.

б) Движение под действием восстанавливающей и постоянной сил

Пусть на точку действует восстанавливающая сила F_вост и постоянная сила F₀. Тогда из (3) имеем

Воспользовавшись (19), получим

                                                                (28)

Дифференциальное уравнение (28) является неоднородным, поэтому его решение ищется в виде

                                                             (29)

где х_общ – общее решение однородного уравнения;

х_част – частное решение.

Так как однородное уравнение – это фактически уравнение (20), то общее решение х_общ можно представить в виде (21) или (22).

Частное решение будем искать в виде

Подставив частное решение в (28), с учетом, что , получим

        

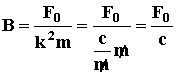
СТАТИЧЕСКОЕ УДЛИНЕНИЕ – это отношение постоянной силы к коэффициенту восстанавливающей силы

Таким образом, окончательно получаем решение уравнения (28) в виде

                                                   (30)

ПРИ ДЕЙСТВИИ ПОСТОЯННОЙ И ВОССТАНАВЛИВАЮЩЕЙ СИЛ МАТЕРИАЛЬНАЯ ТОЧКА БУДЕТ СОВЕРШАТЬ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ, НО ЦЕНТР КОЛЕБАНИЙ БУДЕТ СМЕЩЕН ПО НАПРАВЛЕНИЮ ПОСТОЯННОЙ СИЛЫ НА ВЕЛИЧИНУ СТАТИЧЕСКОГО УДЛИНЕНИЯ.

в) Движение под действием восстанавливающей и силы вязкого трения

СИЛА ВЯЗКОГО ТРЕНИЯ – это сила, прямо пропорциональная скорости материальной точки и направленная против ее движения

где l - коэффициент вязкости.

Тогда уравнение (3) примет вид

Если ввести обозначение , то с учетом (19) это уравнение можно преобразовать к виду

                                                           (31)

Характеристическое уравнение для дифференциального уравнения (31) имеет вид