Механика \ Теоретическая механика

Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 14

Выбирать независимые перемещения можно произвольным образом. Так плоское тело, покоящееся на плоскости (рис. 9), имеет множество возможных перемещений (вправо, влево, вверх под любым углом), но линейно независимых - только три (например, горизонтальное смещение dх, вертикальное смещение вверх dy и угол поворота вокруг точки А - dj).

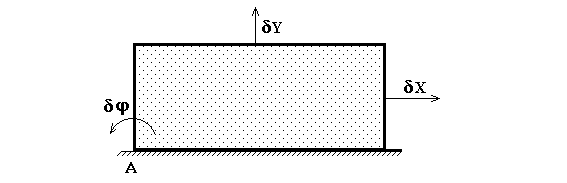
Рис. 9.

Принято обозначать возможные перемещения, указывая символ «δ» перед перемещением.

Следует отличать возможные перемещения от действительных. Возможных может быть множество, а действительных только одно. Действительное перемещение обязательно входит в число возможных.

ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ. Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.

Доказательство. Допустим, система находится в равновесии, т. е. сумма всех сил равна нулю и сумма моментов всех сил равна нулю

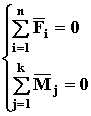
Если умножить оба эти уравнения на любые возможные перемещения δr и δj, а затем сложить эти уравнения, то получим

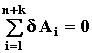
Поскольку все связи в системе идеальные, т.е. работа реакций равна нулю, то остается

ч.т.д. (75)

Теперь рассудим наоборот. Пусть нам известно, что сумма возможных работ активных сил равна нулю. Так как связи идеальные, то получается, что сумма любых возможных мыслимых работ в системе равна нулю. Но действительные перемещения входят в состав возможных и следовательно сумма работ всех сил на действительных перемещениях тоже должна быть равна нулю. А по теореме Д14 это значит, что кинетическая энергия системы тоже равна нулю, откуда вытекает, что все тела системы должны покоится. Ч.т.д.

Принцип возможных перемещений позволяет определять соотношения между силами системы, обеспечивающими ее равновесие, а также любые реакции статически определимых систем. Причем для нахождения одной реакции принцип возможных перемещений всегда позволяет составить ТОЛЬКО ОДНО уравнение, из которого неизвестная реакция будет определена.

Порядок решения задач, использующих

принцип возможных перемещений

1. Вычерчивается расчетная схема задачи.

2. Если требуется определить неизвестную реакцию, то расчетная схема модифицируется таким образом, чтобы система имела возможное перемещение в направлении искомой реакции. Рисуется новая расчетная схема.

3. Системе сообщается любое возможное перемещение (лучше в направлении искомой реакции).

4. Определяются зависимости между сделанным возможным перемещением и происшедшими в результате этого возможными перемещениями точек приложения активных сил.

5. Определяется возможная работа каждой активной точки, причем выражение преобразуется с учетом предыдущего пункта, пока в нем не окажется возможное первичное перемещение как множитель. Обязательно составляется возможная работа для искомой реакции.

6. Возможные работы всех активных сил и искомой реакции суммируются и приравниваются нулю. Поскольку все слагаемые этого уравнения имеют общий множитель – первоначальное возможное перемещение, то его можно сократить и остается уравнение с одной неизвестной реакцией.

УРАВНЕНИЯ ЛАГРАНЖА II-го РОДА

Рассмотрим механическую систему, имеющую n степеней свободы. Каждой степени свободы можно поставить в соответствие одну обобщенную координату. Выбирать обобщенные координаты можно произвольно, но необходимо следить, чтобы они были линейно независимы. Поведение такой механической системы описывается n уравнениями движения. Лагранж впервые их получил в следующей форме

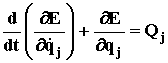
(76)