д) Движение под действием восстанавливающей силы, силы вязкого трения и возмущающей гармонической силы
Уравнение (3) в этом случае имеет вид
![]() (38)
(38)
Без вывода приведем решение уравнения (38)
![]() (39)
(39)
где ![]() общее решение однородного
уравнения, определяемое так, как это изложено в пункте в), т.е. (33) или (35);
общее решение однородного
уравнения, определяемое так, как это изложено в пункте в), т.е. (33) или (35);
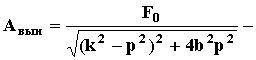 амплитуда вынужденных колебаний;
амплитуда вынужденных колебаний;
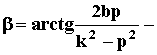 начальная фаза вынужденных
колебаний.
начальная фаза вынужденных
колебаний.
В рассматриваемом случае ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ СКЛАДЫВАЕТСЯ ИЗ ДВУХ ГАРМОНИЧЕСКИХ ДВИЖЕНИЙ – СОБСТВЕННЫХ И ВЫНУЖДЕННЫХ, НО ПОСКОЛЬКУ СОБСТВЕННЫЕ КОЛЕБАНИЯ ЯВЛЯЮТСЯ ЛИБО ЗАТУХАЮЩИМИ, ЛИБО АПЕРИОДИЧЕСКИМИ, ТО ПО ПРОШЕСТВИИ КОНЕЧНОГО ПРОМЕЖУТКА ВРЕМЕНИ ИХ ВЛИЯНИЕ СТАНЕТ ИСЧЕЗАЮЩЕ МАЛЫМ И ПОВЕДЕНИЕ ТОЧКИ БУДУТ ОПРЕДЕЛЯТЬ ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ.
Д В И Ж Е Н И Е М А Т Е Р И А Л Ь Н Ы Х Т Е Л
УРАВНЕНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС СИСТЕМЫ
МЕХАНИЧЕСКАЯ СИСТЕМА – это произвольный заранее выбранный набор материальных тел, поведение которых анализируется.
В дальнейшем будет использоваться следующее правило: В МАТЕМАТИЧЕСКИХ ВЫКЛАДКАХ ХАРКТЕРИСТИКИ МАТЕРИАЛЬНЫХ ТОЧЕК В ОТЛИЧИЕ ОТ ХАРАКТЕРИСТИК МАТЕРИАЛЬНЫХ ТЕЛ, БУДУТ ИМЕТЬ ИНДЕКС.
МАССА ТЕЛА – это сумма масс всех материальных точек, составляющих данное тело
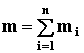
ВНЕШНИЕ СИЛЫ – это силы взаимодействия материальных точек, включенных в механическую систему и не включенных.
ВНУТРЕННИЕ СИЛЫ – это силы взаимодействия материальных точек, включенных в механическую систему.
ТЕОРЕМА Д1. Сумма внутренних сил механической системы всегда равна нулю.
Доказательство. Согласно аксиоме Д5, для любой пары материальных точек механической системы сумма сил их взаимодействия всегда равна нулю. Но все взаимодействующие точки принадлежат системе и, следовательно, любой из внутренних сил всегда найдется противодействующая внутренняя сила. Следовательно, полная сумма всех внутренних сил обязательно равна нулю. Ч.т.д.
ТЕОРЕМА Д2. Сумма моментов внутренних сил механической системы всегда равна нулю.
Доказательство. Согласно аксиоме Д5, каждой внутренней силе найдется противодействующая внутренняя сила. Поскольку линии действия этих сил совпадают, то их плечи относительно любой точки пространства будут одинаковы и, следовательно, их моменты, относительно выбранной точки пространства по величине одинаковы, но знаки имеют разные, так как силы направлены противоположно. Следовательно, полная сумма моментов всех внутренних сил обязательно равна нулю. Ч.т.д.
ТЕОРЕМА Д3. Произведение массы всей механической системы на ускорение ее центра масс равняется сумме всех внешних сил, действующих на систему.
Доказательство. Рассмотрим произвольную механическую систему, состоящую из конечного числа материальных тел. На основании аксиомы Д2 каждое тело можем разбить на конечное число материальных точек. Пусть всего получено nтаких точек. Для каждой такой точки на основании аксиомы Д4 можно составить уравнение движения
![]()
Учитывая, что
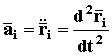 (КИНЕМАТИКА стр. 3), а
также разбив все силы, действующие на i-ю точку, на внешние и внутренние, получим из
предыдущего равенства
(КИНЕМАТИКА стр. 3), а
также разбив все силы, действующие на i-ю точку, на внешние и внутренние, получим из
предыдущего равенства
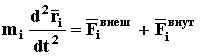
Если просуммировать уравнения движения всех точек системы, получим
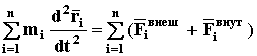
Используя коммутативность операций суммирования и дифференцирования (фактически знаки суммирования и дифференцирования можно менять местами), получим
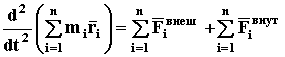 (40)
(40)
Выражение, полученное в скобках, может быть представлено через координату центра масс системы (СТАТИКА стр. 15)
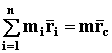
где m – масса всей системы;
![]() - радиус-вектор центра
масс системы.
- радиус-вектор центра
масс системы.
Как следует из теоремы Д1, последнее слагаемое в выражении (40) обращается в ноль, поэтому
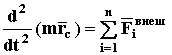
или 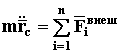 ,
ч.т.д. (41)
,
ч.т.д. (41)
Следствие. Центр масс механической системы движется таким образом, как если бы он был материальной точкой, обладающей всей массой системы и к которой приведены все внешние силы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.