Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 8

Полный ИМПУЛЬС СИЛЫ – это сумма всех элементарных импульсов в течение времени действия силы

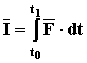
Импульс постоянной силы

Если , то

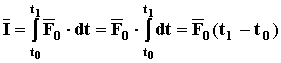
ИМПУЛЬС ПОСТОЯННОЙ СИЛЫ РАВЕН ПРОИЗВЕДЕНИЮ САМОЙ СИЛЫ НА ПРОМЕЖУТОК ВРЕМЕНИ ДЕЙСТВИЯ СИЛЫ.

ТЕОРЕМА Д8 (Первая основная теорема динамики). Изменение количества движения механической системы равно сумме импульсов всех внешних сил, действующих на систему.

Доказательство. Рассмотрим произвольную механическую систему. Она состоит из конечного числа материальных тел. На основании аксиомы Д2 можем разбить каждое тело на конечное число материальных точек. Пусть будет всего n таких точек. Для каждой точки, согласно аксиомы Д4, можно выписать уравнение движения

Разбив все силы, действующие на каждую точку, на внешние и внутренние, а также учитывая определение ускорения (КИНЕМАТИКА стр. 3), получим

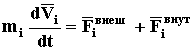
Просуммировав уравнения движения всех точек системы, получим

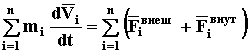
Воспользовавшись коммутативностью свойств операций суммирования и дифференцирования, а также учитывая, что масса - величина постоянная, будем иметь

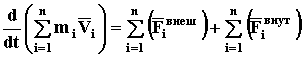
На основании теоремы Д1 последнее слагаемое обращается в ноль. Умножим обе части уравнения на dt

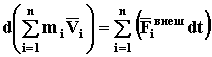
Выражение в скобках слева – это то, что было определено как момент количества движения системы (44), а справа в скобках – элементарные импульсы силы (46)

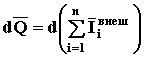                                                          (47а)

Если это выражение проинтегрировать, то получим

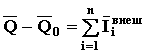                                                         (47б)

Выражение (47а) называют дифференциальной формой теоремы Д8, а (47б) – интегральной. Приведенные формы идентичны, если в задаче требуется определить ускорение, то лучше воспользоваться формулой (47а), если скорости – то (47б).

МОМЕНТ ИНЕРЦИИ ТЕЛА

МОМЕНТ ИНЕРЦИИ ТОЧКИ относительно выбранной оси – это произведение массы точки на квадрат ее расстояния до выбранной оси.

МОМЕНТ ИНЕРЦИИ ТЕЛА относительно выбранной оси – это сумма моментов инерции всех точек тела относительно той же оси

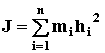                                                                 (48)

СОБСТВЕННЫЙ МОМЕНТ ИНЕРЦИИ ТЕЛА – это момент инерции относительно оси, проходящей через центр масс данного тела.

В справочной литературе всегда приводятся ТОЛЬКО СОБСТВЕННЫЕ моменты инерции.

Моменты инерции некоторых тел

Для наиболее распространенных форм материальных тел собственные моменты инерции определены в более удобном виде, чем формула (48). Приведем некоторые из них. На рисунках показано плоское изображение тел, поэтому ось Z всегда направлена перпендикулярно рисунку.

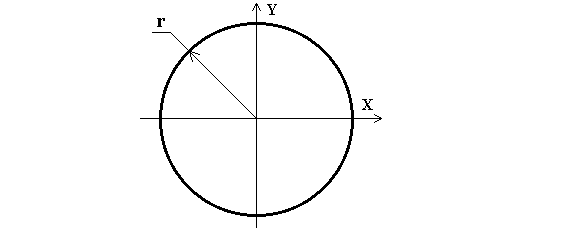
1. Термин: КОЛЬЦО, ОБРУЧ, ПОЛЫЙ ЦИЛИНДР.

Примечание. Масса тела распределена по окружности.

Изображение:

                              

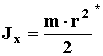
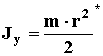
* - кроме цилиндра.

2.  Термин: ДИСК, КРУГЛАЯ ПЛАСТИНА, СПЛОШНОЙ ЦИЛИНДР.

Изображение:

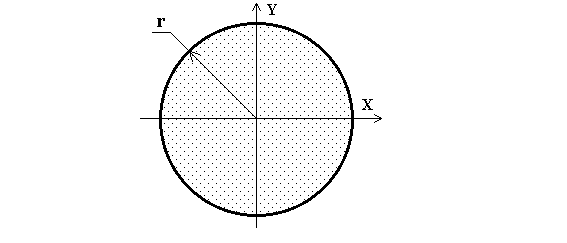
Примечание: Масса тела распределена по всей поверхности.

                             

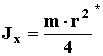
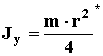
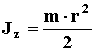
* - кроме цилиндра.

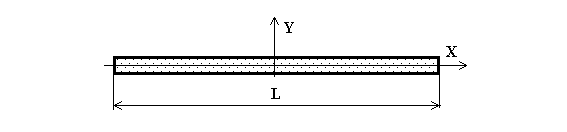
3.  Термин: СТЕРЖЕНЬ, ТЯГА.

Примечание: Любая деталь, у которой один размер больше двух других.

Изображение:

                                      

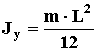
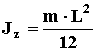
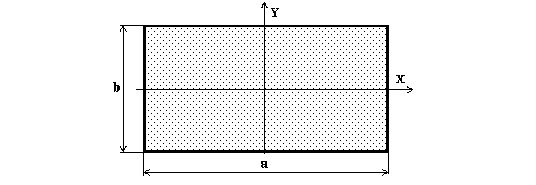
4.  Термин: ПРЯМОУГОЛЬНАЯ ПЛАСТИНА ИЛИ ЛИСТ.

Примечание: Масса тела распределена по всей поверхности.

                          

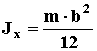
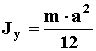
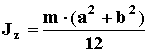
Изображение:

РАДИУС ИНЕРЦИИ – это радиус такого кольца, которое имеет такую же массу и такой же собственный момент инерции, что и данное тело.

Если в задаче задан радиус инерции тела, то вычислять момент инерции следует обязательно по формуле

.

ТЕОРЕМА Д9(Штейнера-Гюйгенса). Момент инерции относительно произвольной оси равен сумме собственного момента инерции относительно оси, параллельной данной, и произведения массы тела на квадрат расстояния от центра масс тела до оси.