Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 13

Следствие 2. Изменение кинетической энергии механической системы с идеальными связями равняется сумме работ всех активных сил, действующих на систему

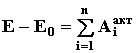                                                           (69)

ПРИНЦИП  Д’АЛАМБЕРА

СИЛА ИНЕРЦИИ МАТЕРИАЛЬНОЙ ТОЧКИ – это условная сила, линия действия которой противоположна действительному ускорению точки и которая равна по величине произведению массы точки на её ускорение

                                                                 (70)

СИЛА ИНЕРЦИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ – это сумма сил инерции всех точек системы

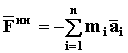                                                             (71)

ТЕОРЕМА Д16. Сила инерции механической системы равняется произведению массы всей системы на ускорение её центра масс, взятое с обратным знаком.

Доказательство. Рассмотрим произвольную механическую систему. На основании аксиомы Д2 разобьем каждое тело системы на материальные точки. Пусть всего получено n таких точек. Для каждой i–ой точки, воспользовавшись определением ускорения и формулой (70), можем написать

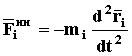
Просуммируем полученное выражение по всем точкам механической системы, получим

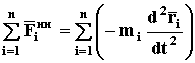
Воспользовавшись свойствами суммирования и дифференцирования, а также формулой (71)

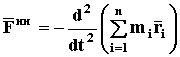
Используя определение центра масс системы (СТАТИКА стр. 15), получим

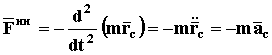                                     (72)

ЦЕНТР ИНЕРЦИИ СИСТЕМЫ – точка приложения силы инерции системы.

Положение центра инерции ищется как точка приложения равнодействующей всех элементарных сил инерции. Следует помнить, что поскольку силы инерции могут вести себя не так, как силы тяжести, то ЦЕНТР ИНЕРЦИИ И ЦЕНТР ТЯЖЕСТИ ТЕЛА МОГУТ НЕ СОВПАДАТЬ.

Для примера рассмотрим ось АВ, вращающуюся в подшипниках А и В с постоянной угловой скоростью (направление вращения показано стрелкой) и расположенную вертикально (рис. 8). К оси АВ приварен стержень CD под некоторым углом. Поскольку стержень вращается равномерно, то каждая i-я точка стержня, удаленная от оси вращения на расстояние h_i, имеет ускорение . Это значит, что силы инерции точек стержня параллельны между собой и пропорциональны расстоянию от точки до оси вращения, т.е. силы инерции стержня являются нагрузкой, распределенной по треугольному закону. Как известно, равнодействующая такой нагрузки приложена на расстоянии одной трети от максимальной. Таким образом, получается, что центр тяжести такого стержня находится посредине (точка Е), а центр инерции - на расстоянии двух третьих длины стержня от оси вращения (точка Н).

ИНЕРЦИОННЫЙ МОМЕНТ – это условный момент, который действует относительно оси вращения тела и равен произведению момента инерции тела относительно этой оси на угловое ускорение тела, взятое с противоположным знаком

                                                                 (73)

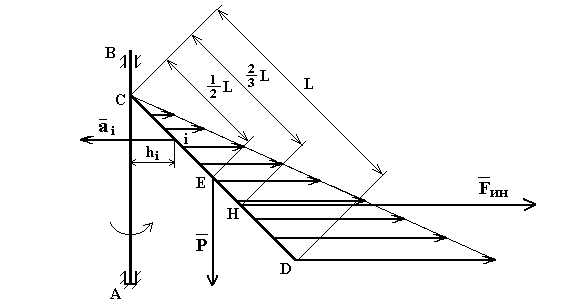
Рис. 8.

ПРИНЦИП Д^’АЛАМБЕРА. Если к заданным внешним силам, действующим в системе, добавить силы инерции тел и их инерционные моменты, то можно считать, что система находится в равновесии.

Доказательство. В общем случае движение материального тела описывается двумя векторными уравнениями

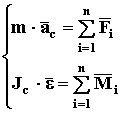
где  ускорение центра масс тела;

J_c – собственный момент инерции тела.

C учетом теоремы Д16 и определения силы инерции (72) и инерционного момента (73)

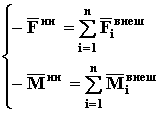
Если собрать все слагаемые в одну часть

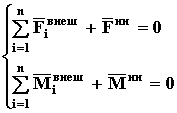                                                     (74)

Получены уравнения, фактически совпадающие с уравнениями описывающими равновесное положение тела, хотя тело находится в движении.

ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ

Термин “ОБОБЩЕННЫЙ” в механике означает “линейный”  или “угловой”,  если связывается с перемещениями, и “сосредоточенная сила” или “момент силы”, если связывается с силами.

ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ СИСТЕМЫ – это количество линейно независимых возможных обобщенных перемещений системы.