Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 5

Его корни определяются выражением

                                                     (32)

В зависимости от подкоренного выражения меняется вид решения уравнения (31). Рассмотрим два случая

1) Пусть , т.е.

Обозначим , тогда

                         

С учетом введенных обозначений решение уравнения (31) можно представить в виде

       (33)

Движение материальной точки по закону (33) называется ЗАТУХАЮЩИМИ КОЛЕБАНИЯМИ. Для этих колебаний характерно следующее.

Во-первых, для различных моментов времени  выполняется соотношение  или .

Во-вторых, период затухающих колебаний

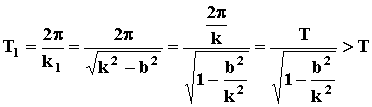
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ ХАРАКТЕРИЗУЮТСЯ ПЛАВНЫМ УМЕНЬШЕНИЕМ АМПЛИТУДЫ И УВЕЛИЧЕНИЕМ ПЕРИОДА КОЛЕБАНИЙ С ТЕЧЕНИЕМ ВРЕМЕНИ.

На рис. 1 показан пример графика затухающих колебаний.

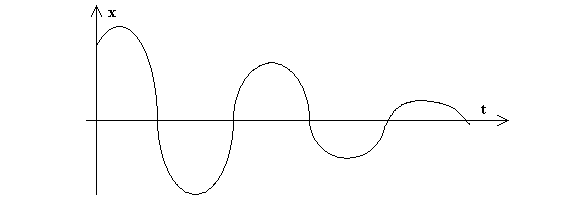
Рис. 1.

Пусть в момент времени

, а при

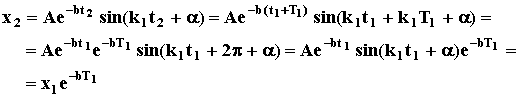
или 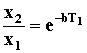                                                                         (34)

Таким образом, размах колебаний образует убывающую геометрическую прогрессию. Знаменатель этой прогрессии, определяемый формулой (34), называется ДЕКРЕМЕНТ КОЛЕБАНИЙ, а величина  ЛОГАРИФМИЧЕСКИЙ ДЕКРЕМЕНТ КОЛЕБАНИЙ.

2) Пусть , т.е. .

Тогда с учетом формулы (32), введенной в предыдущем пункте, решение уравнения (31) ищется в виде

                                                         (35)

Из формулы (32) следует, что корни характеристического уравнения z₁ и z₂ являются отрицательными величинами.

Движение материальной точки, которое происходит по закону (35), называется АПЕРИОДИЧЕСКИМ. В апериодическом движении присутствует фактически только одно полуколебание. Материальная точка просто приближается замедленно к своему равновесному положению. На рис. 2 показаны примеры поведения апериодического закона при различных начальных условиях.

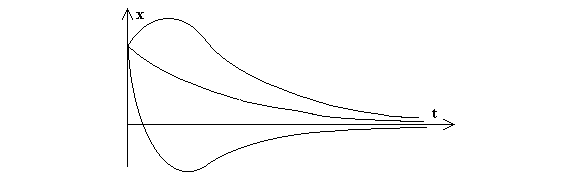
Рис. 2.

ПРИ ДВИЖЕНИИ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ВОССТАНАВЛИВАЮЩЕЙ СИЛЫ И СИЛЫ ВЯЗКОГО ТРЕНИЯ, ЕСЛИ СИЛЫ ВЯЗКОСТИ ДОСТАТОЧНО ВЕЛИКИ, ТО ДВИЖЕНИЕ ТОЧКИ БУДЕТ АПЕРИОДИЧЕСКИМ, А ЕСЛИ МАЛЫ – ТО ЗАТУХАЮЩИМ.

г) Движение под действием восстанавливающей и возмущающей гармонических сил

Выражение для гармонической возмущающей силы имеет вид

где F₀ – амплитуда колебаний возмущающей силы;

р – частота колебаний возмущающей силы.

Тогда уравнение (3) примет вид

Учитывая замену (19), получим

                                                       (36)

Решение уравнения (36) ищется в виде (29), причем общее решение однородного уравнения уже получено (20), а частное решение  будем искать в виде

где В – неизвестная константа.

Учитывая

из (36) можем получить

Так как эта формула должна быть верна для любого момента времени, то, сократив общий множитель , получим

     или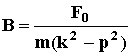      

Окончательно решение уравнения (36)примет вид

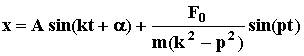                               (37)

ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ВОССТАНАВЛИВАЮЩЕЙ И ВОЗМУЩАЮЩЕЙ СИЛ ЯВЛЯЕТСЯ СУММОЙ ДВУХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ: С ЧАСТОТОЙ k (СОБСТВЕННЫЕ КОЛЕБАНИЯ) И ЧАСТОТОЙ р (ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ).

Обратим внимание на второе слагаемое в (37). Если частота вынужденных колебаний оказывается близка к частоте собственных (), то амплитуда вынужденных колебаний при отсутствии других сил неограниченно возрастает

Значительное увеличение амплитуды вынужденных колебаний без увеличения возмущающей силы называется РЕЗОНАНС.

Резонанс является одним из важнейших феноменов механики. С одной стороны, он очень вреден для жестких конструкций. В самолетостроении, кораблестроении, моторостроении и т.д. проектировщики тратят массу сил и средств, добиваясь того, чтобы собственные частоты конструкции в целом и отдельных ее узлов не были близки частотам внешних нагрузок. А с другой стороны, движение механизма в режиме резонанса требует минимальных затрат энергии на поддержание движения (только компенсация затрат на преодоление сил трения). Это особенно важно для механизмов, работающих в режиме периодического движения, т.е. «разгон – торможение – выстой – разгон …» (двигатели, конвейеры, прессы, средства механизации, роботы и т.д.). При этом и разгон, и торможение требуют затрат энергии, которые в случае резонансного движения будут минимальны. Энергетические ресурсы нашей планеты (нефть, уголь, газ) не безграничны и человечеству рано или поздно придется больше уделять внимания ресурсосберегающим технологиям. Поэтому у резонансных механизмов большое будущее.