Динамика: Конспект лекций по курсу "Теоретическая механика" (Уравнения движения материальной точки в декартовой системе координат. Уравнения движения материальной точки в естественной системе координат), страница 15

-  “замораживаем” (обездвиживаем) все обобщенные координаты кроме той, для которой собираемся подсчитать обобщенную силу;

-  задаем системе возможное перемещение по этой обобщенной координате;

-  подсчитываем работу всех действующих в системе сил на сделанном возможном перемещении;

-  суммируем эти работы;

-  поскольку все слагаемые в полученной сумме содержат сомножителем сделанное возможное перемещение, то его можно вынести за скобку.

То выражение, которое останется в скобках, и является обобщенной силой , соответствующей рассмотренной обобщенной координате.

ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ

Если воспользоваться принципом Д^,Аламбера и принципом возможных перемещений для произвольной механической системы, то можем сформулировать следующее утверждение.

ТЕОРЕМА Д16. Сумма возможных работ всех сил, действующих в произвольной механической системе, а также возможных работ всех сил инерции и инерционных моментов всегда равна нулю

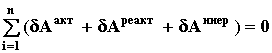                                     (77)

Доказательство. Без доказательства.

РЕКОМЕНДАЦИИ ПО СОСТАВЛЕНИЮ УРАВНЕНИЙ

ДВИЖЕНИЯ ПРИ РЕШЕНИИ ЗАДАЧ ДИНАМИКИ

Подводя итоги рассмотренного курса динамики, следует сказать, что решение обратной задачи динамики представляет серьезную трудность из-за необходимости выполнять операцию интегрирования. Поэтому были разработаны различные подходы к решению этой задачи (закон изменения импульса, закон изменения кинетической энергии и т.д.), с которыми мы познакомились. Сформулируем рекомендации по решению задач динамики.

Если в задаче речь идет о движении материальной точки, то

-  если движение сложное, то следует использовать уравнения (17);

-  если известна траектория движения материальной точки, то следует использовать уравнения (16);

-  если траектория неизвестна, то уравнения (2).

Если в задаче речь идет о движении материального тела, то

-  если тело движется поступательно, то используются уравнения (43);

-  если тело движется вращательно, то используется уравнение (58);

-  если тело движется плоскопараллельно, то используются уравнения (59).

Если в задаче идет речь о движении системы тел (два тела уже система) с одной степенью свободы, то

-  если все тела системы двигаются поступательно, то следует пользоваться первой основной теоремой динамики (47), а если в каком-либо направлении силы уравновешены и в начальный момент система покоилась, то можно использовать уравнение (42);

-  если все тела системы двигаются поступательно, но хотя бы одно вращательно, то следует пользоваться второй основной теоремой динамики (57);

-  если все тела системы двигаются поступательно или вращательно, но хотя бы одно плоскопараллельно, то следует пользоваться третьей основной теоремой динамики (69), с учетом (70) и (71).

Следует помнить, что третья основная теорема динамики может подвести там, где происходит мгновенная передача движения (ударное взаимодействие тел: пуля попадает в доску, молот бьет по наковальне и т.д.). В этом случае лучше использовать первую, либо вторую основные теоремы.

Если по условию задачи не требуется искать характеристики движения отдельных тел, то удобно использовать (39), с учетом (40) и (41).

Если в задаче идет речь о движении системы со многими степенями свободы, то следует использовать уравнения Лагранжа (78), либо общее уравнение динамики (79).

Если в задаче идет речь об исследовании состояния равновесия, то следует пользоваться либо уравнениями статики, либо принципом возможных перемещений (77).

Если в задаче требуется подсчитать динамические реакции в точках крепления тел, то обязательно следует использовать принцип Д’Aламбера (76).

В любом из всех вышеперечисленных случаев следует учитывать, что после подстановки в уравнения движения заданных сил и разделения переменных, по виду полученного уравнения можно выписать решение уравнения в соответствующем в