Структурный анализ и кинематическое исследование механизма, определение сил и моментов сил инеции, страница 12

3.3 Определение момента инерции маховика.

После построения диаграммы разности работ DА (приращения кинетической энергии DT) и приведенной массы всего механизма строится диаграмма кинетической энергии в функции приведенной массы DT – m_пр(DT – I_пр) – диаграммы Виттенбауэра.

tg y_max=V²_срk_m/2K_t(1+d)=6,1

y_max=80,7

tg y_min= V²_срk_m/2K_t(1-d)

y_min=79,9

Маховой момент маховика определяется по выражению:

GD²=3600 K_t*АВ/dn²=69,5 кг*м²

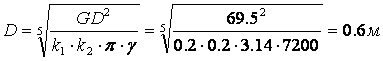
a=k₁*D=0,12 мм

b=k₂*D=0,12 мм

4. СИНТЕЗ ЭВОЛЬВЕНТНОГО ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ

Исходные данные

Числа зубьев сопряженных колес z₁=12 ; z₂=24 ; модуль  m=15 мм ;  угол профиля a=20° ; коэффициент высоты зуба  h_a=1;  коэффициент радиального зазора c=0,25

Коэффициент смещения исходного контура  x₁=0, x₂=0 выбраны по табл     [1].

Основные параметры передачи и размеры зубьев сопряженных зубчатых колес для передачи определяются по следующим формулам:

1. Радиусы делительных окружностей

r₁=m*z₁/2=15*12/2=90 мм

r₂=m*z₂/2=15*24/2=180 мм

2. Радиусы основных окружностей

r_b1=r₁*cosa=84,57 мм

r_b2=r₂*cosa=169,15 мм

3. Делительный окружной шаг

P_t=p*m=47,12 мм

4. Делительная окружная толщина зуба

S_t1=p*m/2+2x_1*m*tga=26,84 мм

S_t2=p*m/2+2x_2*m*tga=20,29 мм

5. Угол зацепления

inva_w=2(x₁+x₂) tga/(z₁+z₂)+ inva=inva

a_w=a=20

6. Межосевое расстояние

a_w=m*(z₁+z₂)/2 =270 мм

7. Радиусы начальных окружностей

r_w1=a_w/(u+1)=90 мм