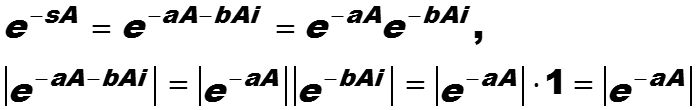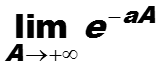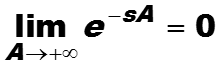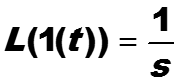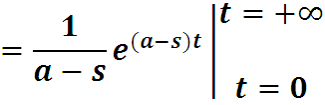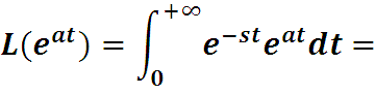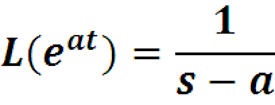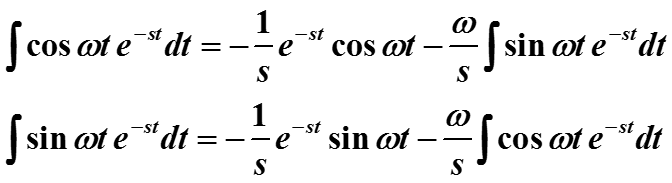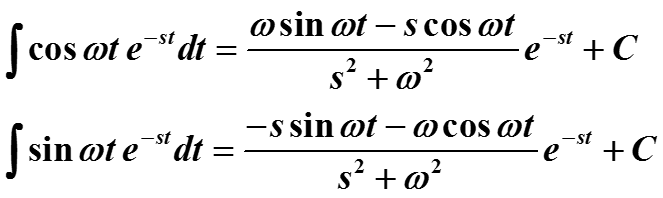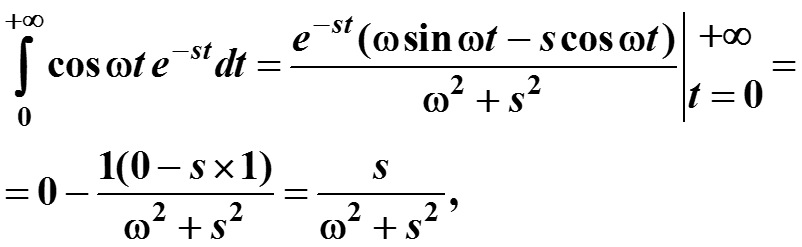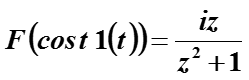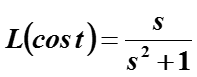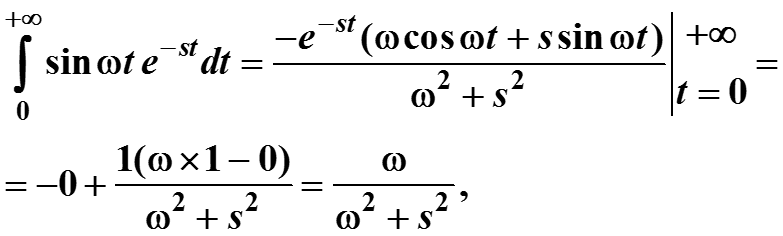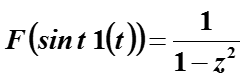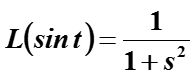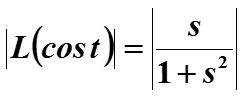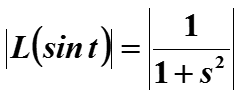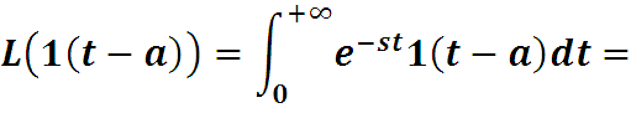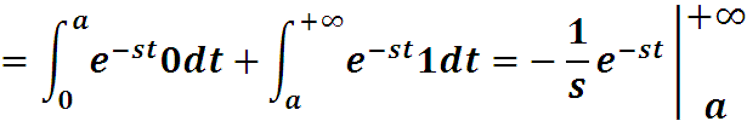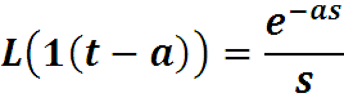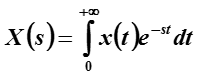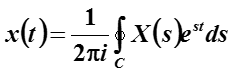Преобразование Лапласа. Решение дифференциальных уравнений преобразованием Лапласа. Обратное преобразование Лапласа

6. Преобразование Лапласа

1

6. Преобразование Лапласа

6.2. Преобразование Лапласа. 6.3. Решения дифференциальных уравнений преобразованием Лапласа. 6.4. Обратное преобразование Лапласа. 6.5. Непрерывные и дискретные преобразования. 6.6. z-преобразование. 6.7. Свойства z-преобразования. 6.8. Обратное z-преобразование. 6.9. Анализ и проектирование фильтров. 6.10. Инвариантный метод анализа фильтра. 6.11. Решение уравнений в конечных разностях.

2

6.2. Преобразование Лапласа

• Преобразование Лапласа приме-няется в радиоэлектронике, а также для исследования дифференциальных уравнений.
• Оно преобразует дифференци-альное уравнение в алгебраиче-ское, которое обычно решается проще. Затем полученное в часто-тной области решение обратным преобразованием Лапласа пере-водится в решение исходного дифференциального уравнения.

3

6.2. Преобразование Лапласа

L{ f(t)} = F(s)

Дифференц уравнение f(t)

Алгебраическое уравн F(s)

Прямое

L-1{F(s)} = f(t)

Решение алг уравнения F(s)

Решение диф уравнение f(t)

Обратное

4

6.2. Преобразование Лапласа

• Преобразованием Лапласа F(s) функции f(t), определенной для t ≥ 0, называется интегральное преобразование:
  • для вычисления такого интеграла применяются те же приемы, что и для преобразования Фурье.
  • Переменная s комплексная, переменная t тоже может быть комплексной.
  • Преобразование Лапласа – это оператор L[·] от функции f(t), точнее, это интегральный оператор от f(t).

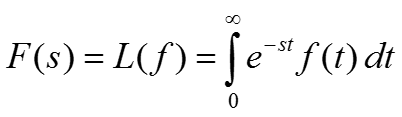
5

6.2. Преобразование Лапласа

• Пример. Найти преобразование Лапласа функции единичного скачка (Хевисайда)

• Решение.

• Это табличный интеграл

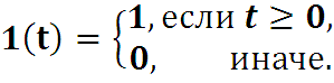
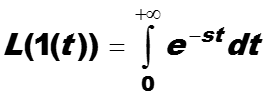
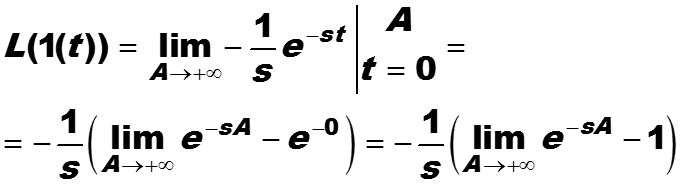
6

6.2. Преобразование Лапласа

• s – комплексное число, пусть

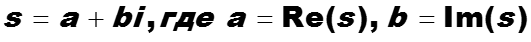
• Тогда модуль комплексного числа

• Если a < 0, то предел

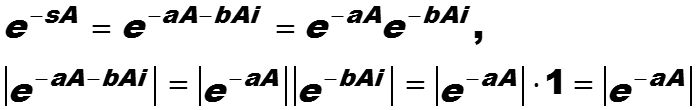
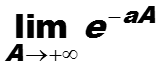
не существует, его значение уходит на бесконечность.

• Если a > 0, то предел

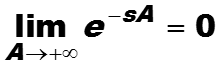
так как модуль экспоненты стремится к нулю.

7

6.2. Преобразование Лапласа

• При s = 0 преобразование Лапласа сигнала 1(t) не определено, (почему?). Таким образом преобразование Лапласа сигнала 1(t) определено для параметров s таких, что Re(s) > 0 . В этом случае

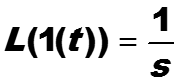
• На комплексной плоскости область параметров s, для которых преобразование Лапласа сигнала 1(t) определено имеет вид

Im(s)

Re(s)

0

8

6.2. Преобразование Лапласа

• Пример. Найти преобразование Лапласа функции eat
• Решение не представляет никаких трудностей:
• Если Re (a-s) > 0, то значение определенного интеграла уходит на бесконечность, то интеграл не существует.
• Если Re (a-s) = 0, то интеграл от константы также равен бесконечности, то есть не существует.
• При Re (a-s) < 0 интеграл существует, преобразование равно

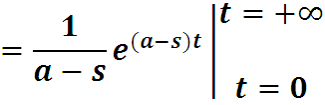
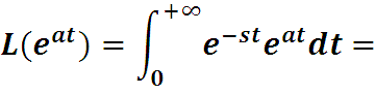
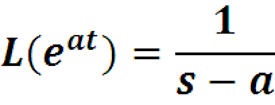
9

6.2. Преобразование Лапласа

• Пример. Найти преобразование Лапласа тригонометрических функций cos ωt и sin ωt с параметром ω≠0.
• Интегрирование по частям дает :

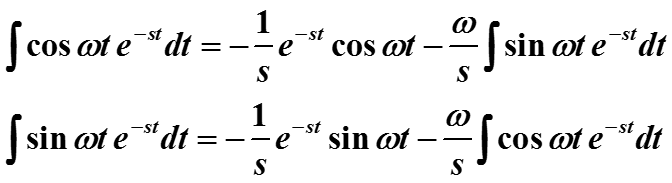
• Подставляем в первую формулу второе выражение и решая полученное уравнение, имеем результат :

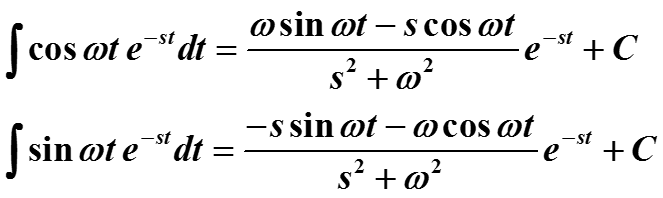
10

6.2. Преобразование Лапласа

• Теперь для сигнала Cos ωt :

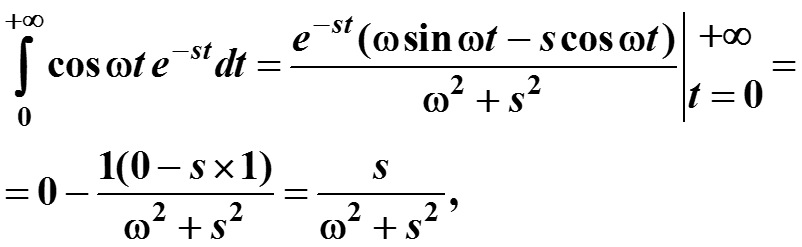
• интеграл существует, если Re(s)>0.

11

6.2. Преобразование Лапласа

• Сравним преобразования Фурье и Лапласа от Cos ωt , преобразование Фурье вычислим также на интервале [0, +∞]

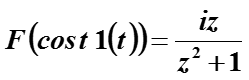
(вычисляется как Фурье от произведения)

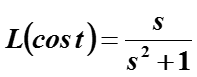
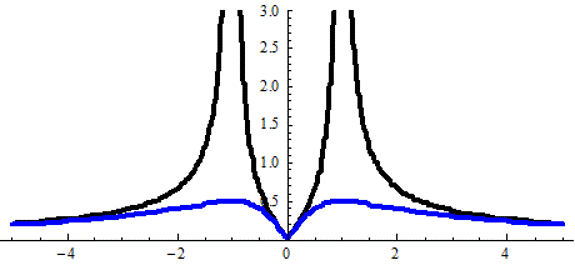
Графики АЧХ от Cos(t) при применении Фурье- и Лаплас преобр.

12

6.2. Преобразование Лапласа

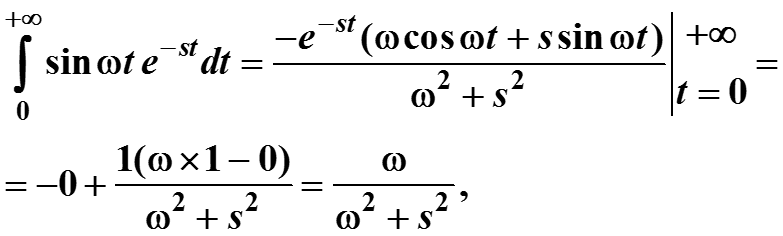
• интеграл существует, если Re(s)>0.

Ну, это совсем просто! Француз, наверное, брал по частям ? Только что такое Re(s) ? Что-то музыкальное ?

13

6.2. Преобразование Лапласа

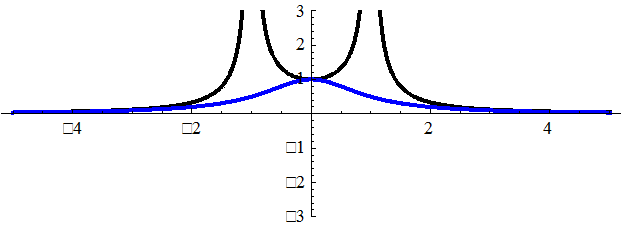
• Сравним преобразования Фурье и Лапласа от sin t , преобразование Фурье вычислим также на интервале [0, +∞]

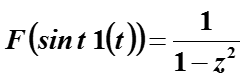
(вычисляется как Фурье от произведения)

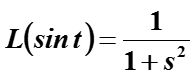
Графики АЧХ от sin t при применении Фурье- и Лаплас преобр.

14

6.2. Преобразование Лапласа

• График АЧХ cos ωt для преобразования Лапласа при ω=1

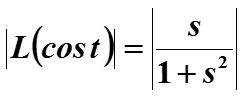
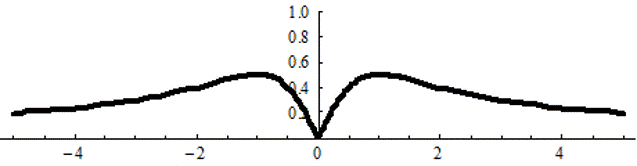
• График АЧХ sin ωt для преобразования Лапласа при ω=1

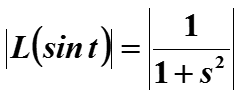
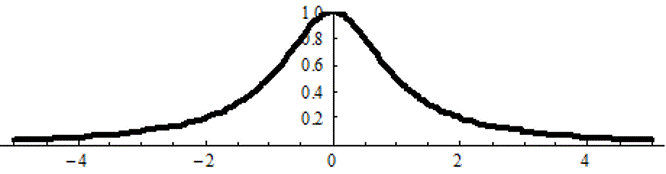
15

6.2. Преобразование Лапласа

• Найдем преобразование Лапласа для функции Хевисайда 1(x-a) со сдвигом на a>0 – сдвиг графика вправо.
• Если Re s > 0, то интеграл сходится и

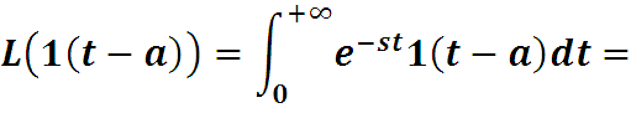
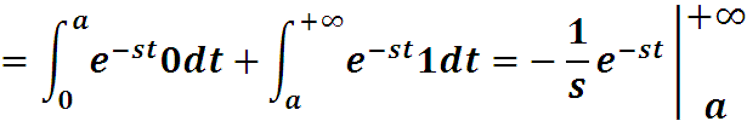
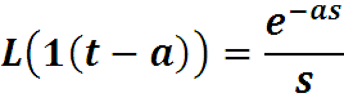
16

6.2. Преобразование Лапласа

• Упражнения.
• 1. Найти преобразование Лапласа для функции f(t) = t.
• 2. Найти преобразование Лапласа для функции f(t) = tn.

• Сравнить преобразование Лапласа от cos(t) и sin(t) с преобразованием Фурье от 1(t)cos(t) и 1(t)sin(t) (использовать правило преобразования Фурье от произведения).

17

6.2. Преобразование Лапласа

Существуют таблицы преобразования Лапласа для различных функций

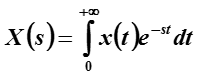
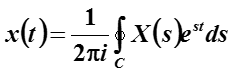
18

6.2. Преобразование Лапласа

• Свойства преобразования Лапласа
• 1. Линейность: L(a·f(t) + b·g(t)) = a·L(f(t)) + b·L(g(t)).
• 2. Свойство сдвига по частоте : если Re (s-a) > 0 и
• L(f) = F, то
• L(eat f(t)) = F(s-a).
• 3. Преобразование производной (Дифференциальное свойство):
• если для некоторого вещественного α>0 функция f(t) ограничена экспонентой:
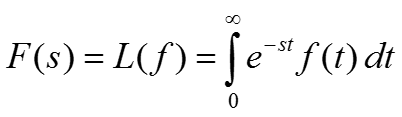
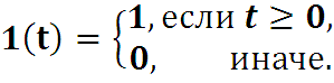
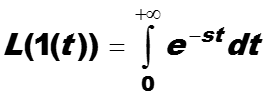
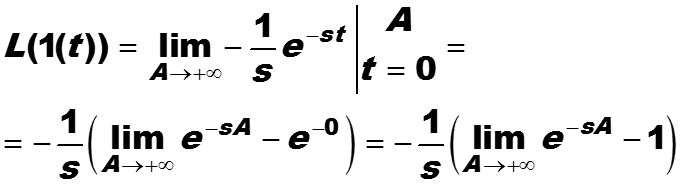