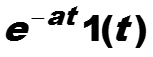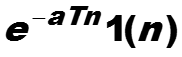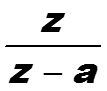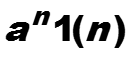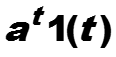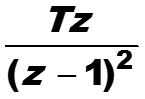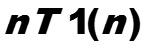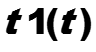Преобразование Лапласа. Решение дифференциальных уравнений преобразованием Лапласа. Обратное преобразование Лапласа, страница 6

• Дифференциальное уравнение можно приближенно записать в виде разностного уравнения.
• Рассмотрим вопрос о том, как найти выходной сигнал y(t), зная разностное уравнение и значения входного сигнала x(t), то есть как решить разностное уравнение.

63

6.6. z-преобразование

• Положит T = 1 и применим к дискретному сигналу f(n) z-преобразование, переводом разностного уравнения в частотную область можно получить его решение.

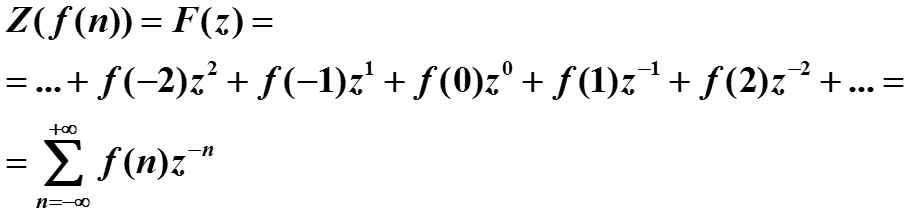
• В общем случае z – комплексная переменная.
• Выполним z-преобразование для нескольких примеров.

64

6.6. z-преобразование

• Пример. Найти z-преобразование сигнала δ1(t).

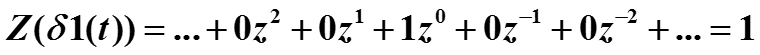
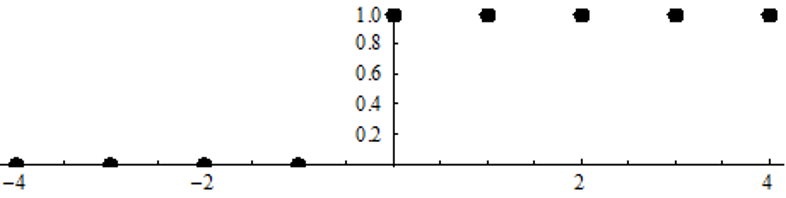
• Пример. Найти z-преобразование дискретной функции Хевисайда :

• График этой функции

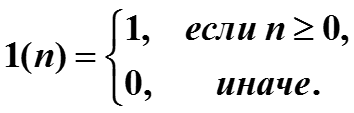
65

6.6. z-преобразование

• Если |z| > 1, то Z(1(n)) равно

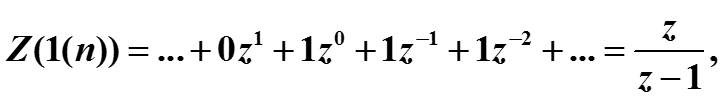
• Если |z| ≤ 1, z-преобразования для 1(n) не существует.
• Пример. Найти z-преобразование сигнала , а > 0.

• Положим тогда

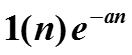
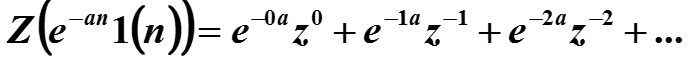
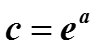
66

6.6. z-преобразование

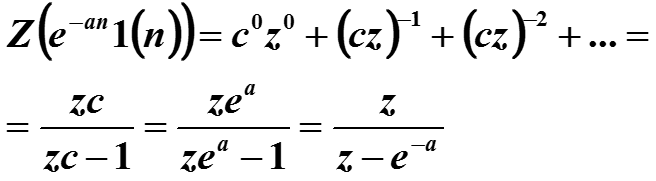
• если знаменатель геометрической прорессии по модулю меньше единицы, то есть, если |z| > e-a .
• Аналогично получается

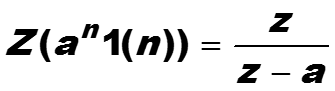
• Это преобразование существует, если |z| > a-1 .

67

6.6. z-преобразование

• Пример. z-преобразование степенных функций nk1(n)
• Построим рекурсивную формулу z-преобразований, рекурсия проводится по степени k. Если известна форму-ла зависимости преобразования для nk1(n) от n(k-1)1(n), то вычисление формулы для nk1(n) можно выполнить следующим способом.
• Для k = 0 степенная функция представляет собой просто дискретную функцию Хевисайда, для 1(n) z-преобразо-вание известно, оно вычисляется как сумма геометричес-кой прогрессии.
• По формуле зависимости находим z-преобразование для k = 1, от него для k = 2, затем для k = 3 и так далее до нужной степени k.

68

6.6. z-преобразование

• Пример. z-преобразование степенных функций
• По определению z-преобразования:

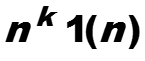
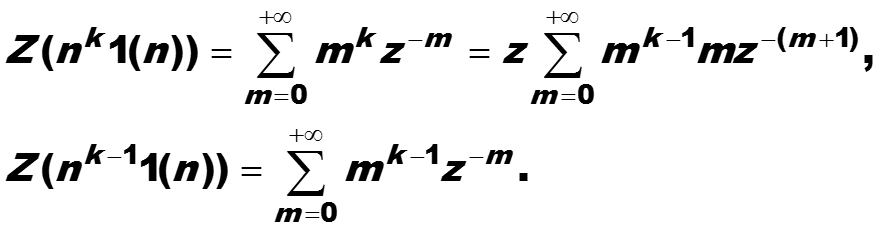
• Предполагая, что все ряды, участвующие в преобразованиях, сходятся абсолютно, дифференцируем по z второе равенство:

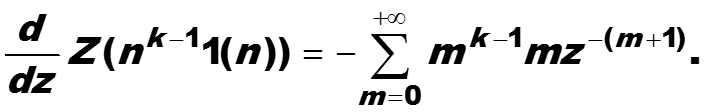
69

6.6. z-преобразование

• Сравнивая (*) с производной, получаем

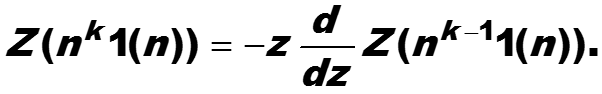
• Это выражение позволяет рекурсивно, начиная с k = 0, найти z-преобразования сигнала для любых по-
• ложительных целых k. Так, для k = 1

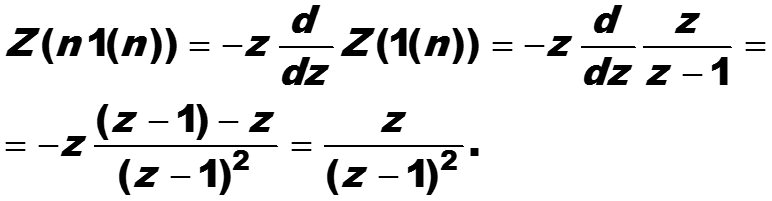
70

6.6. z-преобразование

• Пример (преобразование тригонометрических функций). Найти z-преобразование сигнала
• Представим косинус в комплексной форме (формула Эйлера) и воспользуемся преобразованием экспонент.

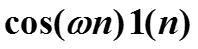
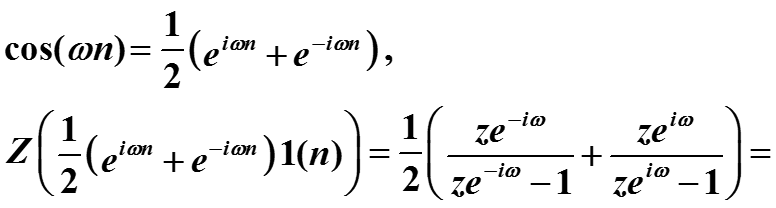
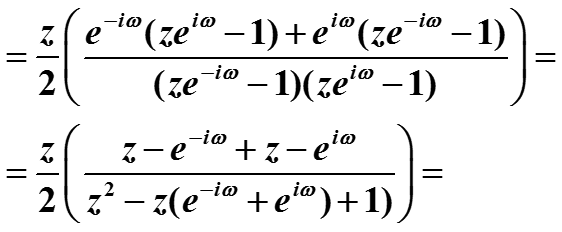
71

6.6. z-преобразование

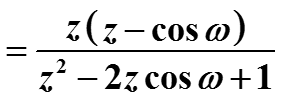
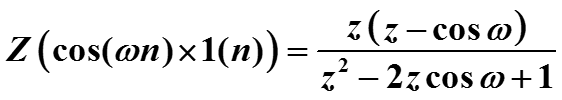
• Аналогично получается z-преобразование сигнала

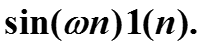
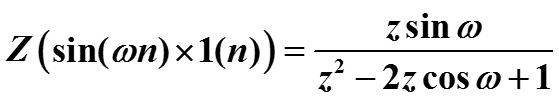
72

6.7. Свойства z-преобразования

• 1. Линейность
• Z(a f(n) + b g(n)) = a F(z) + b G(z)
• 2. Свойство сдвига (задержки)
• Z(f(n-n0)) = F(z) z -n0
• 3. z-преобразование свертки
• Если y(n) – свертка сигналов x1(n) и x2(n) , то
• Y(z) = X1(z) X2(z)

73

6.7. Свойства z-преобразования

• Свойство сдвига. Найти z-преобразование сигнала со сдвигом f(n - n0), если Z(f(n))=F(z).

• Сравним два ряда

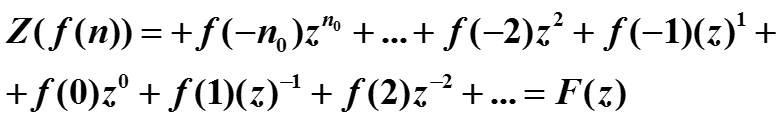
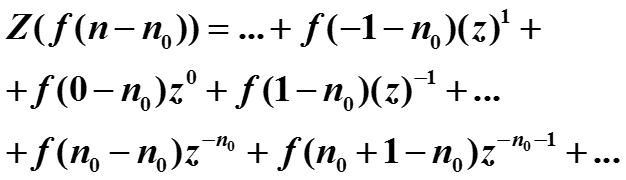
• Предполагая, что ряды сходятся абсолютно, первый ряд, равный F(z), умножим на z-n0 и получим второй ряд. То есть

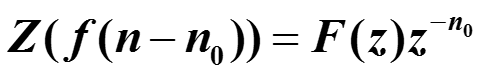
74

6.7. Свойства z-преобразования

• Сверткой двух дискретных сигналов x1(n) и x2(n), где n пробегает целые числа от -∞ до +∞, называется сигнал

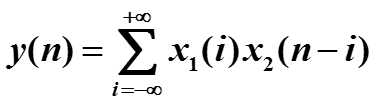
• z-преобразование свертки. Если ряды, представляющий z-преобразования сигналов x1(n) и x2(n) сходятся абсолютно, то z-преобразование свертки равно произведению z-преобразований исходных сигналов :
• Y(z) = X1(z) X2(z)
• Утверждение доказывается перестановкой членов ряда.

75

6.7. Свойства z-преобразования

• Доказательство.

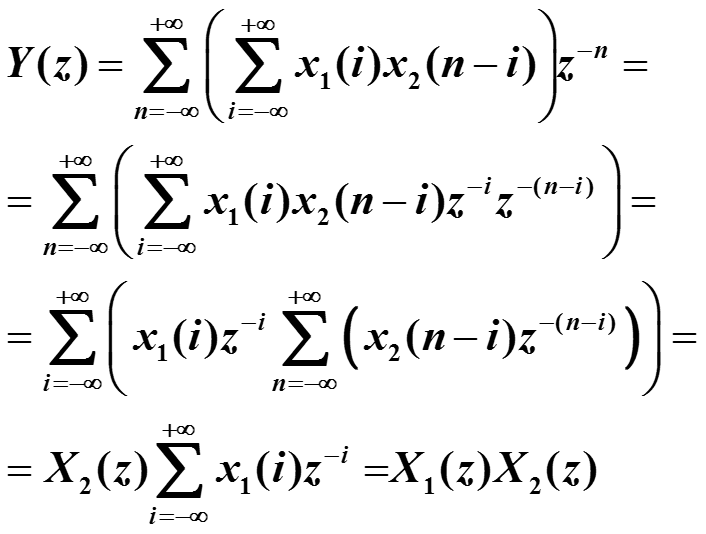
76

6.7. Свойства z-преобразования

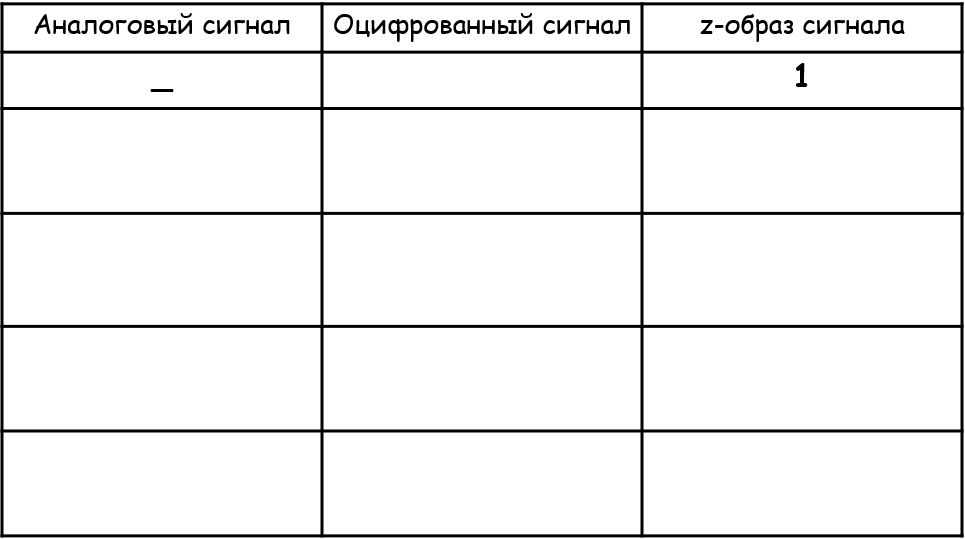
Таблица z-преобразования (1)

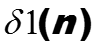
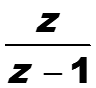
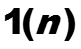
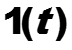
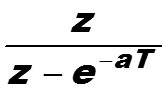
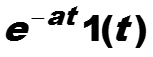
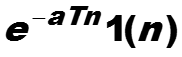
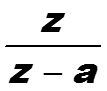
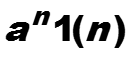
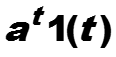
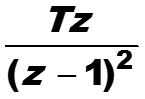
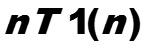
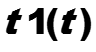
77

6.7. Свойства z-преобразования
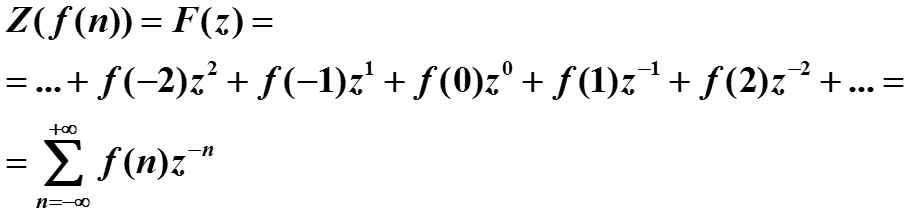
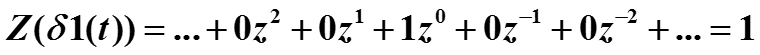
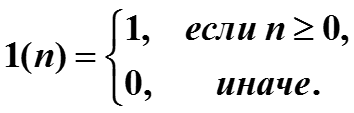
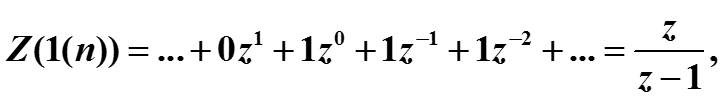
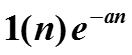
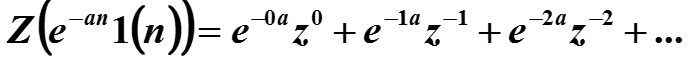
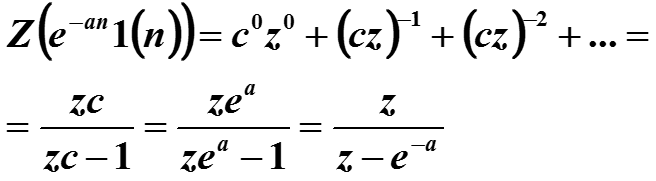
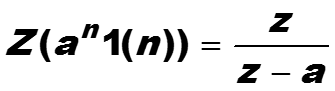
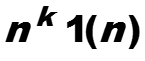
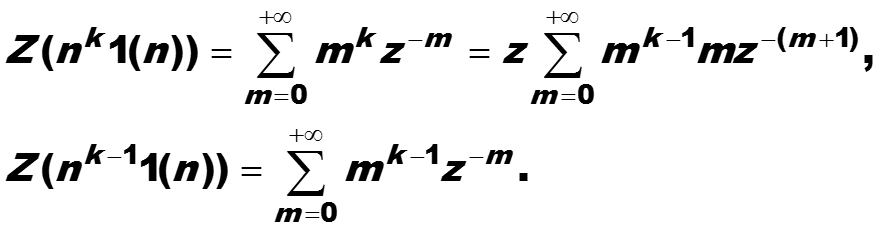
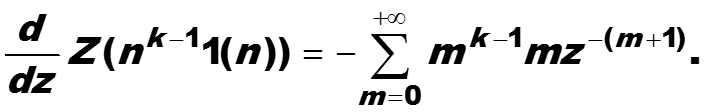
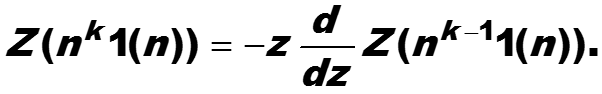
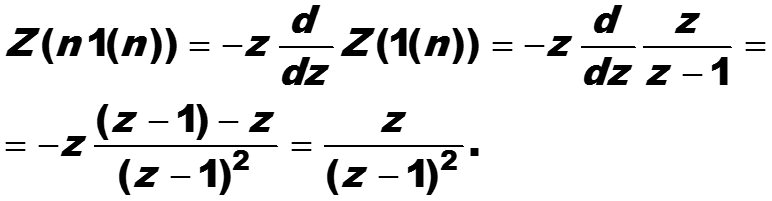
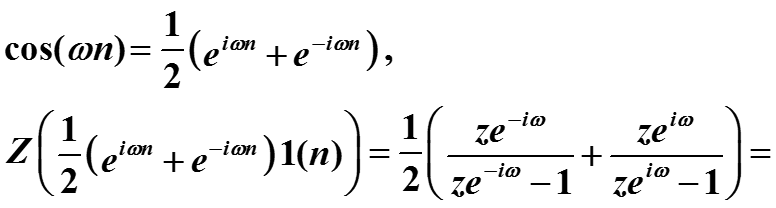
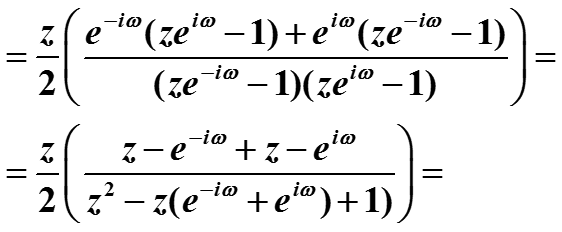
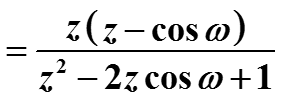
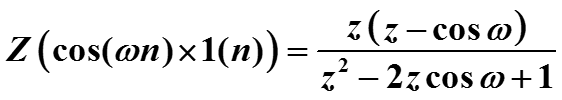
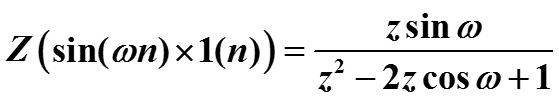
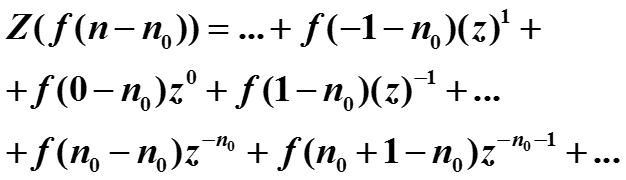
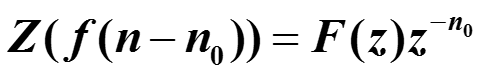
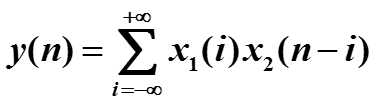
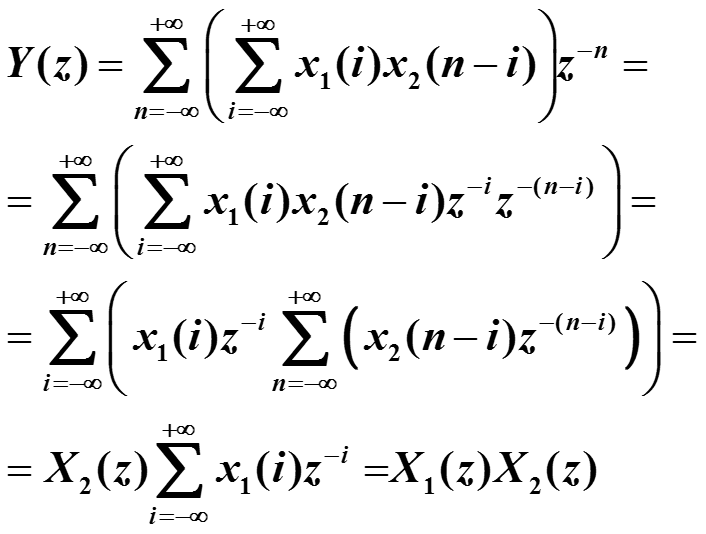
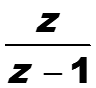
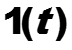
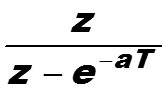