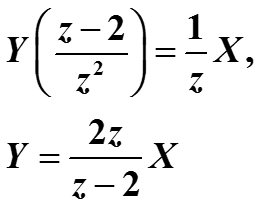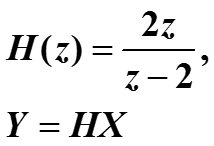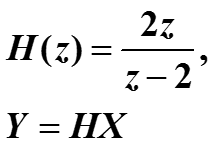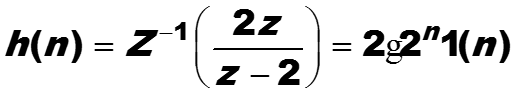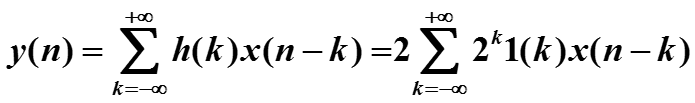-
В инвариантном методе для построения передаточной функции H(•) предлагается в качестве входного параметра X(•) выбрать сигнал, образ которого равен функции Хевисайда, т.е. X(s) = 1(s) или X(z) = 1(z). Мы сосредоточимся только на дискретизированных сигналах и будем принимать во внимание дискретные сигналы y(n) и h(n). Тогда, если y(t) - прообраз функции Y(s), то
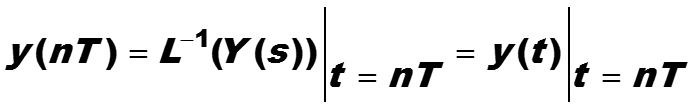
-
Так как ввиду выбора входного сигнала передаточная функция H(•) совпадает с выходным сигналом Y(•) , то аналогичное равенство справедливо и для H(•) :
99
6.10. Инвариантный метод анализа фильтра
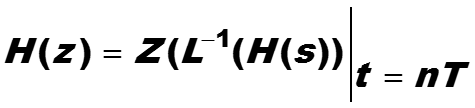
-
Так можно построить передаточную функцию H(z) и найти для нее частотные коэффициенты усиления в требуемых частотных диапазонах. Кроме того, этот подход позволяет построить дискретный фильтр по аналоговому.
-
Пример. Найти коэффициент усиления аналогового фильтра
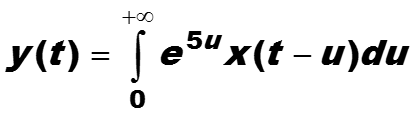
в диапазоне частот 55 – 60 рад/с.
100
6.10. Инвариантный метод анализа фильтра
-
Решение. В частотной области из свертки во временной области получаем произведение сигналов:
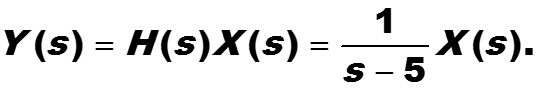
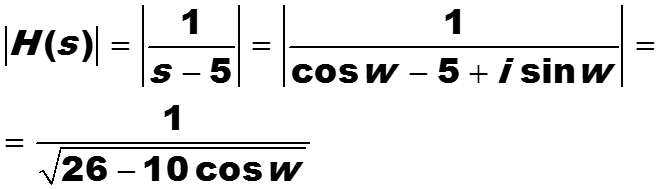
Для оценки коэффициента усиления в качестве переменной s выбираем синусоидальный сигнал

и вычисляем модуль передаточной функции H(s)
101
6.10. Инвариантный метод анализа фильтра
-
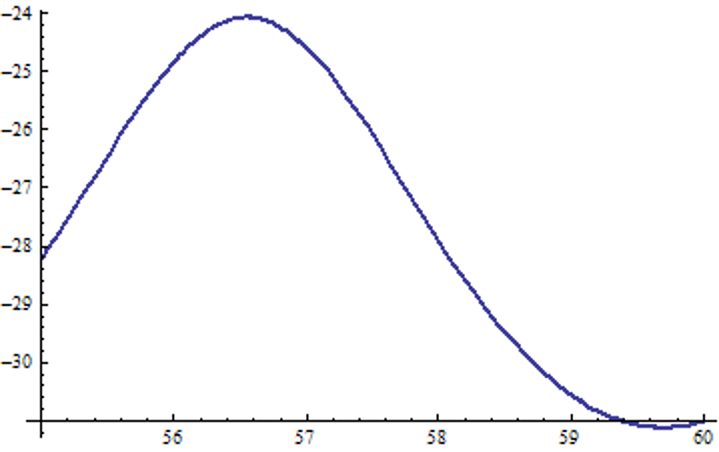
График коэффициента усиления фильтра (в dB)
-
На частотах 55 – 60 рад/с фильтр практически ничего не пропускает
102
6.10. Инвариантный метод анализа фильтра
-
Из этого аналогового фильтра построим инвариантным методом дискретный фильтр в том же диапазоне. Во-первых, найдем интервал дискретизации. Наибольшая частота диапазона равна 60 рад/с. Тогда интервал дискретизации равен
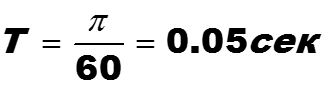
z-преобразование дискретизированной передаточной функции равно
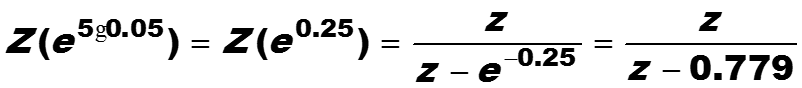
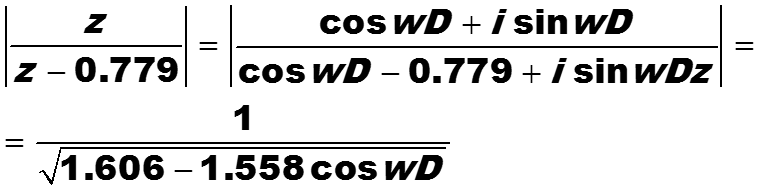
находим модуль последнего выражения
103
6.10. Инвариантный метод анализа фильтра
104
6.10. Инвариантный метод анализа фильтра
-
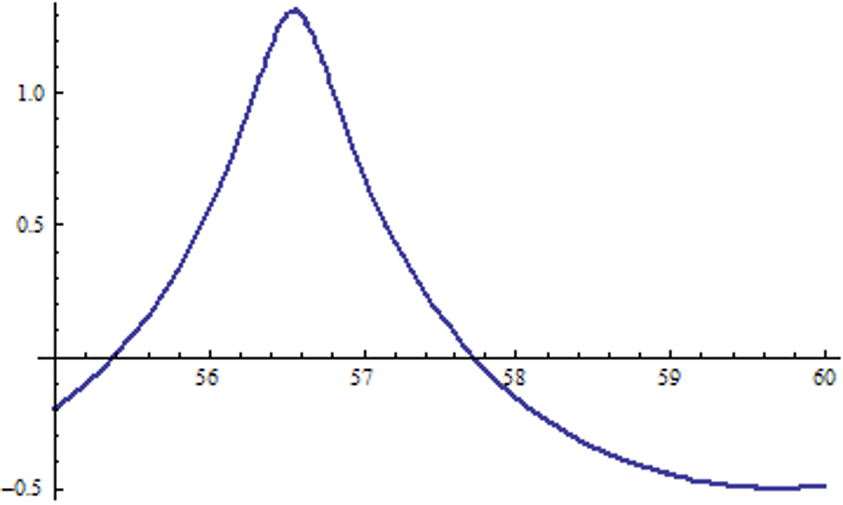
График коэффициента усиления дискретного фильтра (в dB)
105
6.10. Инвариантный метод анализа фильтра
-
Пример. Построить разностное уравнение дискретного фильтра с передаточной аналоговой функцией
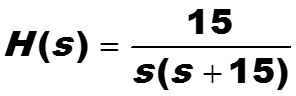
с периодом дискретизации T = 0.05 с.
-
Вначале построим передаточную функцию соответствую-щего дискретного фильтра
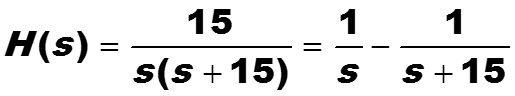
106
6.10. Инвариантный метод анализа фильтра
-
По таблицам преобразования Лапласа и z-преобразова-ния находим соответствующий дискретный фильтр
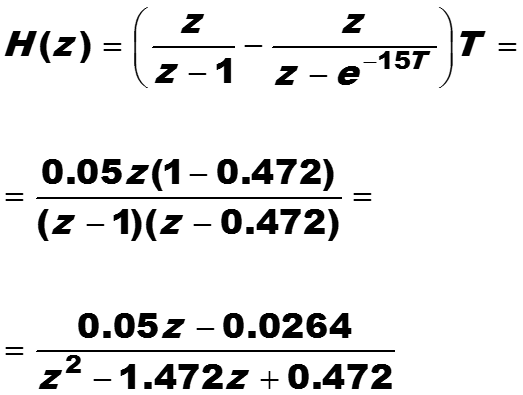
107
6.10. Инвариантный метод анализа фильтра
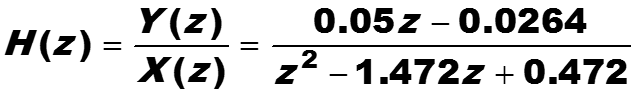
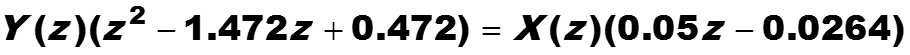
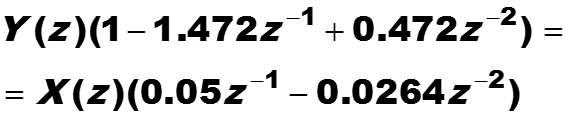
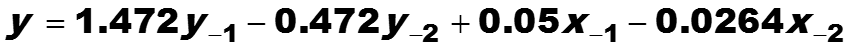
108
6.11. Применение z-преобразования для решения уравнений в конечных разностях
-
Свойство сдвига позволяет решать уравнения в конечных разностях, например,имеем уравнение
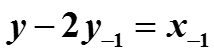
-
Если взять z-преобразование от обеих частей уравнения, то получим уравнение в частотной области

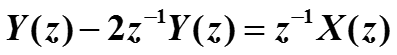
-
Решим его относительно Y, считая X заданным
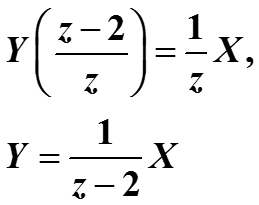
109
6.11. Решение уравнений в конечных разностях
-
Свойство сдвига позволяет решать уравнения в конечных разностях, например,имеем уравнение
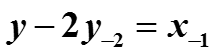
-
Если взять z-преобразование от обеих частей уравнения, то получим уравнение в частотной области
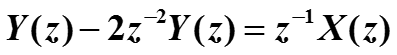

-
Решим его относительно Y, считая X заданным
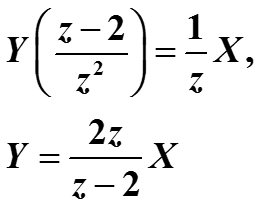
110
6.11. Решение уравнений в конечных разностях
-
Теперь при заданном x(n) остается найти X(z) и обратное преобразование от обеих частей последнего равенства. Так будет получена явная формула для выходного сигнала y(n). Можно находить обратное z-преобразование через интеграл, исходя из определения. Проще, считая, что оно существует, строить обратное z-преобразование по таблице – это инженерный подход.
-
Другой метод анализа выходного сигнала заключается в исследовании функции, преобразующей z-образ входного сигнала X(z) в z-образ выходного сигнала Y(z), она называется передаточной функцией и обозначается через H(z).
-
В нашем примере это функция
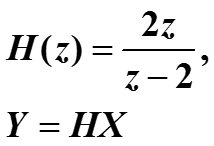
111
6.11. Решение уравнений в конечных разностях
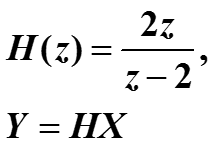
-
Обратное преобразование от передаточной функции равно
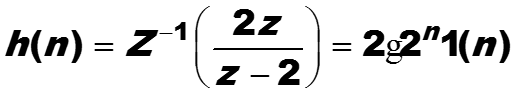
-
По свойству z-преобразования выходной сигнал будет равен дискретной свертке передаточной функции и входного сигнала.
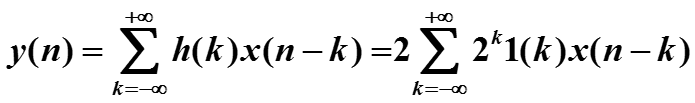
-
В частных случаях дискретную свертку можно упростить.
112
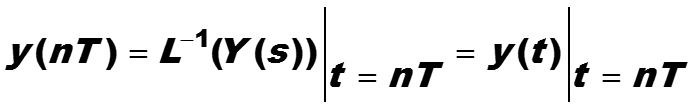
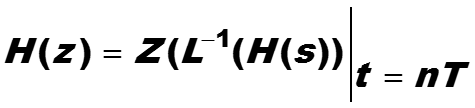
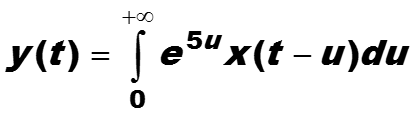
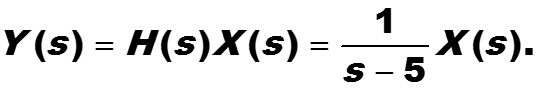



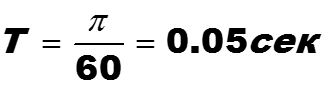
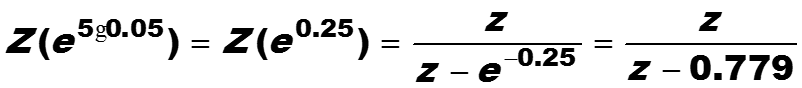


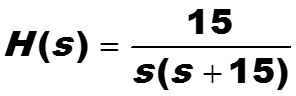
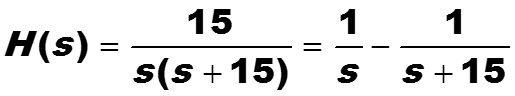
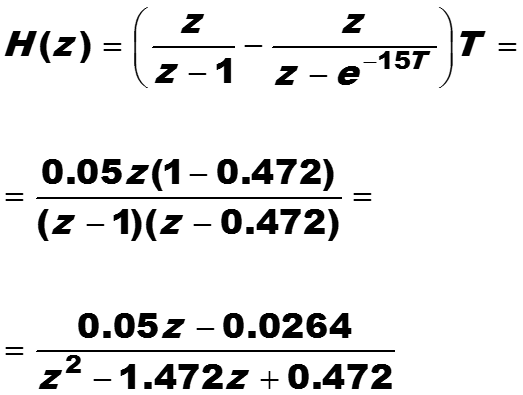
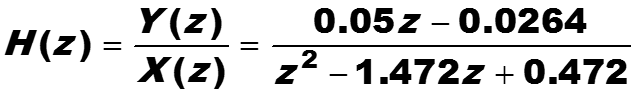
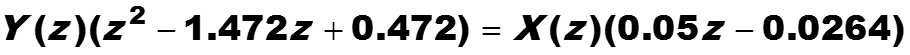
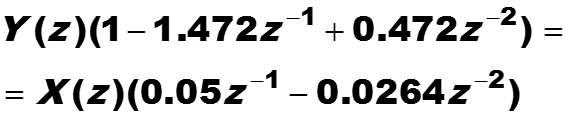
![]()
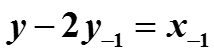
![]()
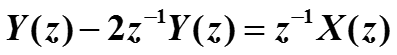
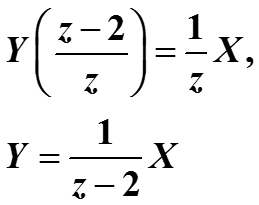
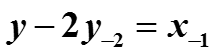
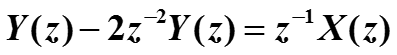
![]()