-
в качестве переменной z выбирают синусоидальный сигнал с аргументом времени t = 1 и переменной частотой. Этот синусоидальный сигнал равен


-
переменной здесь является частота w , множителем служит D. Рассмотрим выбор D.
88
6.9. Анализ и проектирование фильтров
-
Дискретизация по времени T диск и по соответствующей частоте wдиск .
-
Для аналогового сигнала период дискретизации T диск определяется интервалом осцилляции сигнала и по критерию Найквиста равен самое большее (максимум)
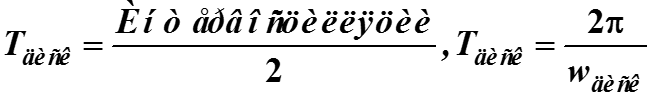

-
где wдиск – частота дискретизации сигнала равна самое меньшее (минимум) удвоенной частоте сигнала wf на интервале его осцилляции.
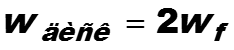
-
где wf – максимум частоты сигнала, учитываемый в решаемой задаче.
89
6.9. Анализ и проектирование фильтров
x(t)
t
0
Tдиск
T0
T1

-
При интервале дискретизации T диск изменение сигнала на интервале T0 учесть нельзя,
-
на интервале T1 изменение сигнала учитывается.
-
T0 < T диск ; T1 > T диск
90
6.9. Анализ и проектирование фильтров
-
Соотношение величины интервала дискретизации T диск с учитываемым интервалом осцилляции T1
-
и соотношение величины частоты дискретизации wдиск с учитываемой частотой w1 предствлены на графиках
t
0
Учитываемые периоды

Tдиск
T1
w
0
wдиск
w1
Учитываемые частоты
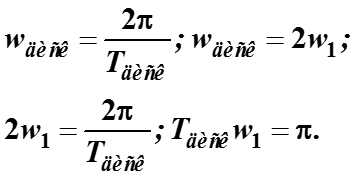
91
6.9. Анализ и проектирование фильтров
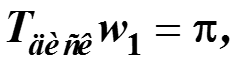
-
При анализе и синтезе цифрового фильтра полагают постоянная D = T диск и вводят замену u = wD и рассматривают изменение аргумента u только на интервале [0, π] или его подмножестве. Таким образом,

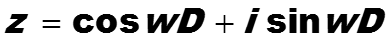
-
где аргумент w пробегает значения в интервале [0, w1 ], при замене аргумента w на u, новый аргумент u пробегает значения в интервале [0, π].
-
Аргумент u применяется для исследования фильтров при помощи z-преобразования.
92
6.9. Анализ и проектирование фильтров
-
Кроме того, следует заметить, что z - образ сигнала рассматривается в частотной области, переменная z является непрерывной комплексной переменной, изменяющейся в своей допустимой области. Дискретиза-ции z-образа не требуется, множитель D – всего лишь удобный множитель, но не интервал дискретизации.
-
Вернемся к примеру анализа усиления сигнала.
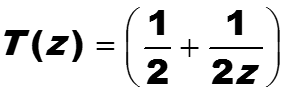
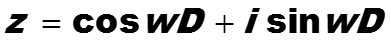
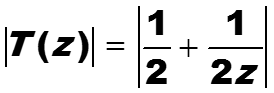
93
6.9. Анализ и проектирование фильтров
-
Вначале найдем модуль передаточной функции
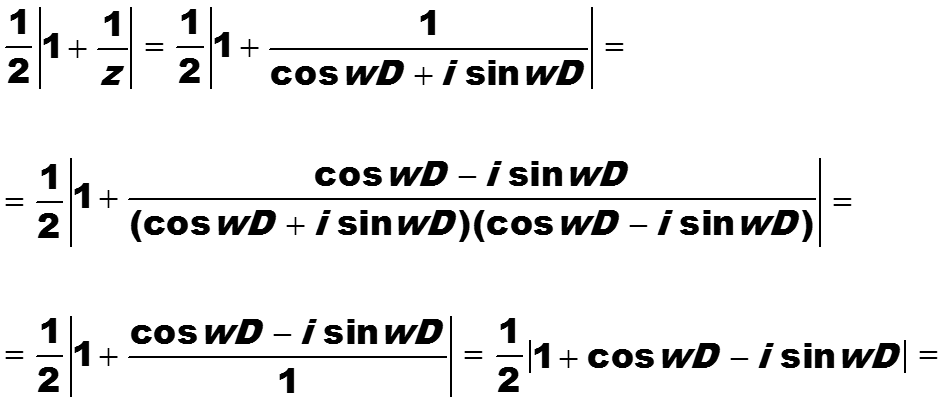
94
6.9. Анализ и проектирование фильтров
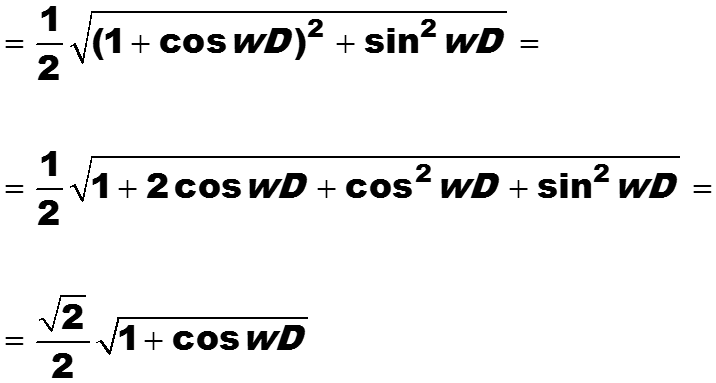
-
Найдем усиление сигнала в диапазоне
-
[200, 600 рад/с] = [32, 96.5 Hz]
95
6.9. Анализ и проектирование фильтров
-
Найдем интервал дискретизации
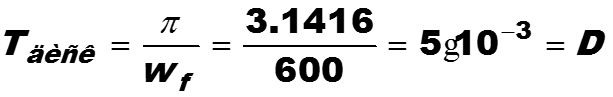
-
Построим график передаточной функции

-
где u изменяется в интервале [0, π]. Но ставилась задача нахожде-ния коэффициента усиления в интервале [200, 600] рад/c. Поэтому нижнее значение переменной u будет равно u0 = 200 5 10-3 = 1. то есть изменения u равен [1, π].
96
6.9. Анализ и проектирование фильтров
-
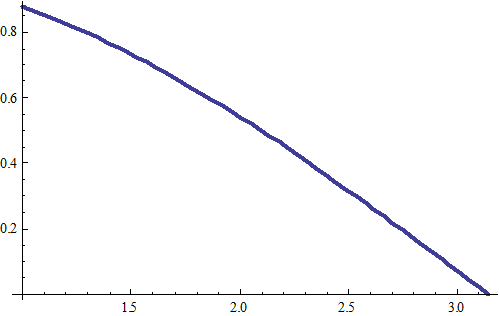
График коэффициента усиления фильтра
-
В качестве среднего можно интеграл от этой функции (она положительная) на заданном интервале, и разделить его на длину отрезка интегрирования. Получаем величину 0.30, в децибеллах коэффициент равен
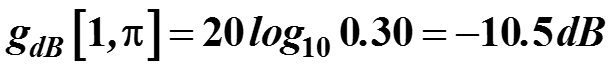
97
6.10. Инвариантный метод анализа фильтра
-
В этом методе анализа фильтра применяется и преобразование Лапласа и z – преобразование.
-
Инвариантный метод применяется для фильтров, у которых в частотной области справедлива зависимость выходного сигнала в виде произведения Лаплас-образов передаточной функции и входного сигнала

-
Если дискретизировать сигналы, то для z-образов будет выполняться аналогичное соотношение
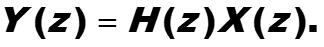
-
Для анализа фильтра нужно исследовать передаточную функцию H(s) – в преобразовании Лапласа и H(z) – в z- преобразовании.
98
6.10. Инвариантный метод анализа фильтра
![]()

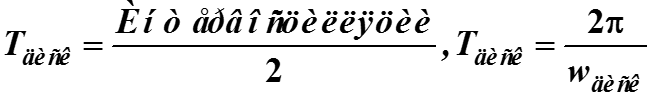
![]()
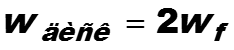
![]()
![]()
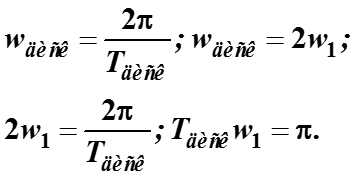
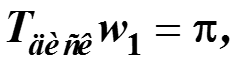
![]()
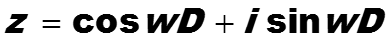
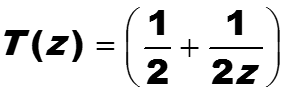
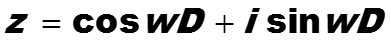
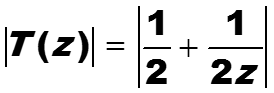
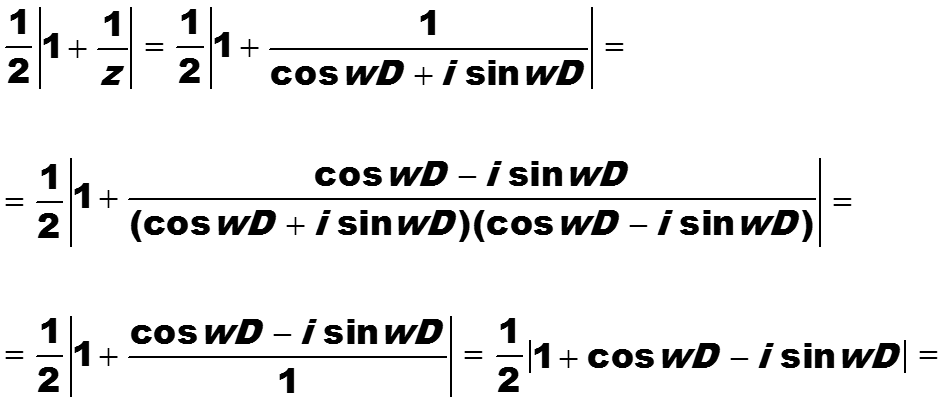
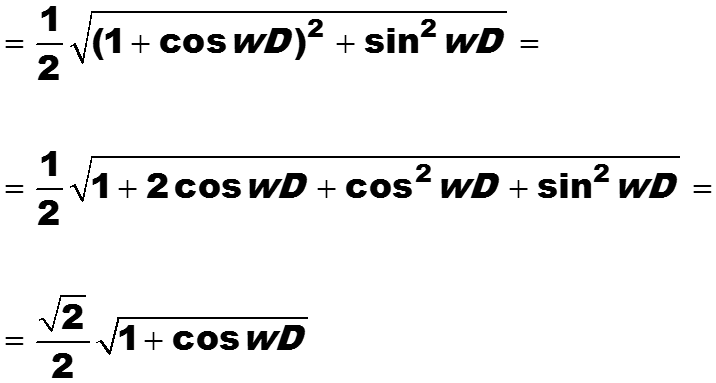
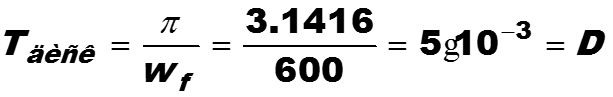


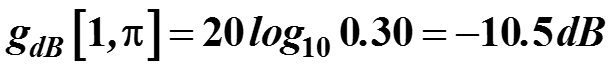
![]()
![]()