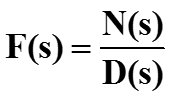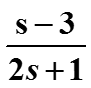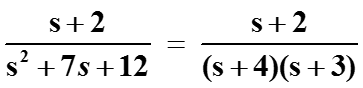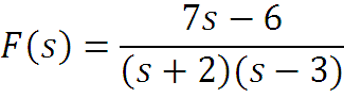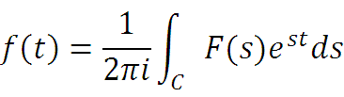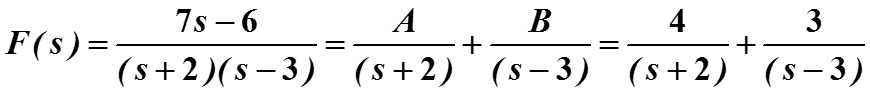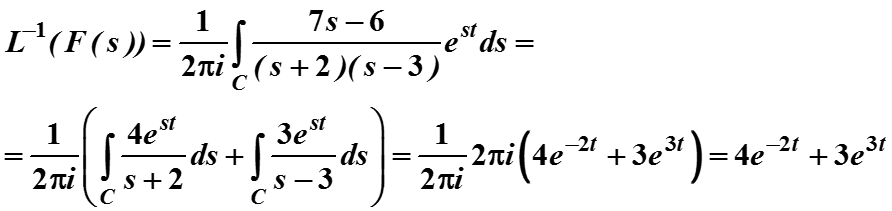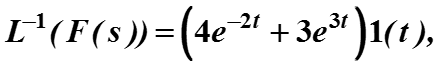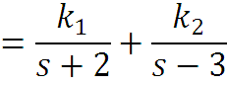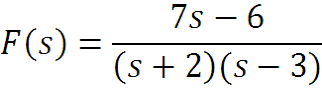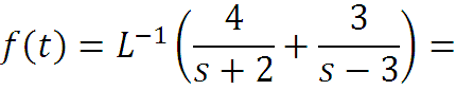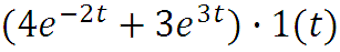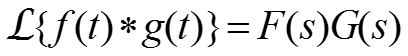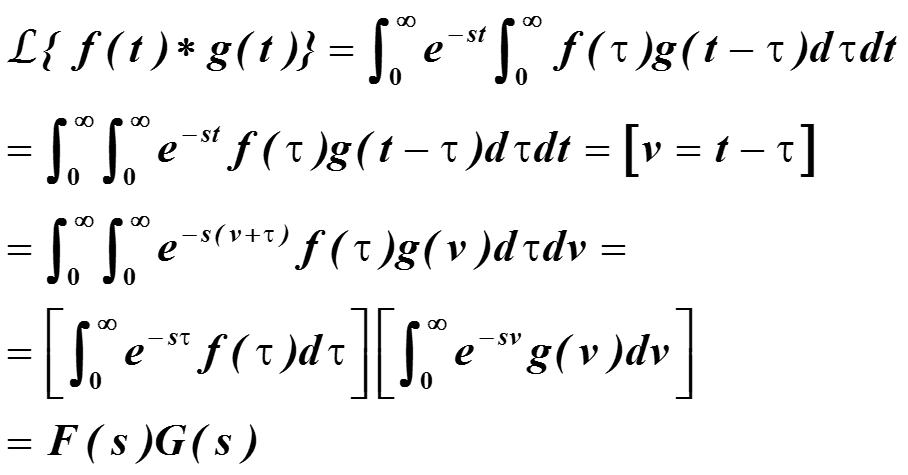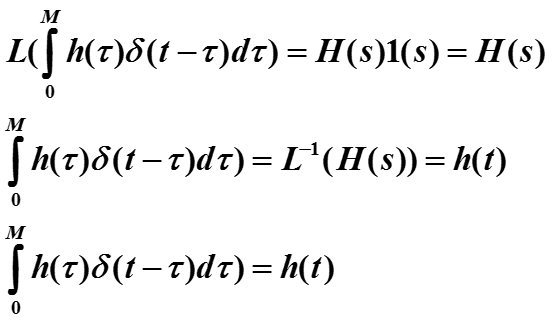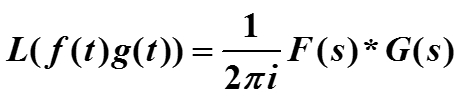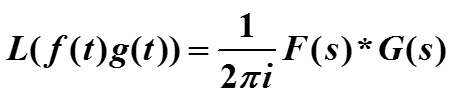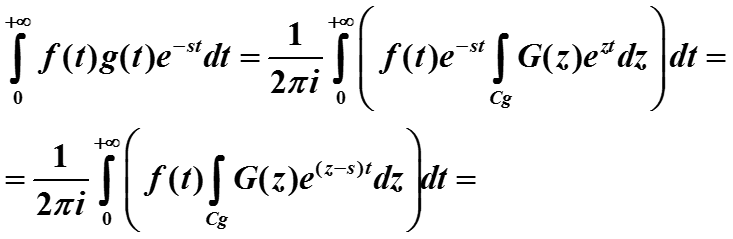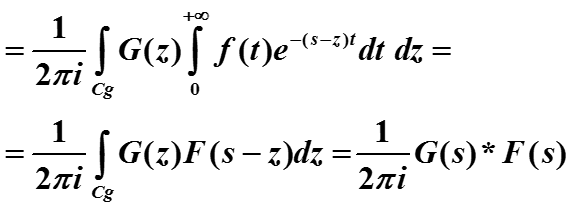Обратное преобразование Лапласа от рациональной функции.
Функция F(s) называется рациональной, если
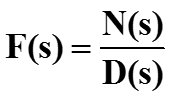
где N(s) и D(s) – многочлены от переменной s. Значения s, для которых N(s) = 0 называются нулями функции F(s), значения s, для которых D(s) = 0 называются полюсами функции F(s). Рациональная функция с точностью до множителя полностью описывается множествами своих нулей и полюсов.
Для функции
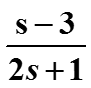
полюс : -1/2; нуль : 3
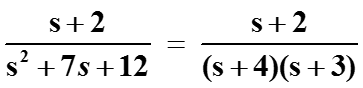
полюса : -4, -3; нуль : -2
6.4.Обратное преобразование Лапласа
-
Пример. Найти обратное преобразование Лапласа функции
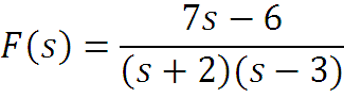
-
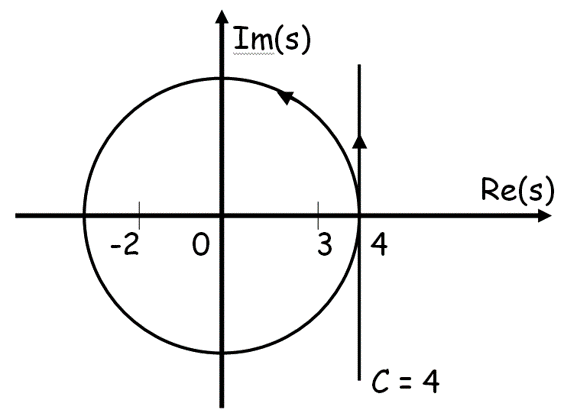
Для этого нужно вычислить интеграл
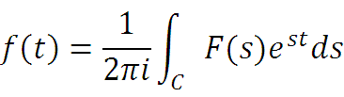
46
6.4.Обратное преобразование Лапласа
-
Вычисление этого интеграла затруднительно, но можно воспользоваться теоремой Коши об интегрировании.
-
F(s) разлагается в сумму простых дробей,
-
коэффициенты (в нашем случае A, B ) вычисляют решением линейных уравнений.
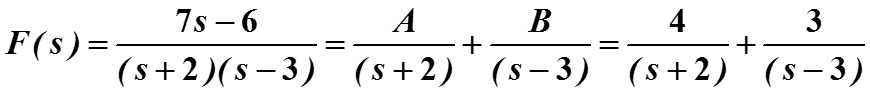
-
Экспоненциальный множитель нигде не обращается в бесконечность, поэтому не добавляет новых полюсов функции F(s).
-
Поэтому по теореме Коши
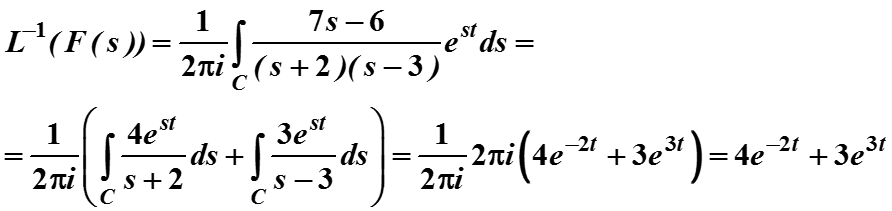
-
Исходная функция, зависящая от времени, согласно прямому преоб-разованию Лапласа, учтена только для t >= 0, для t < 0 функцию обычно зануляют.
47
6.4.Обратное преобразование Лапласа
-
Окончательно обратное преобразование можно записать в виде
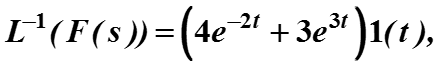
-
здесь исходный сигнал для t < 0 занулен.
48
6.4.Обратное преобразование Лапласа
-
Рациональную функцию F(s) интегрируют простыми правилами.
-
1) F(s) разлагается в сумму простых дробей,
-
коэффициенты (в нашем случае k1, k2 ) вычисляют решением линейных уравнений.
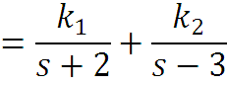
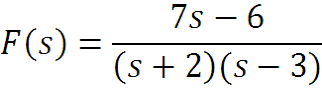
-
2) Для вычисления преобразования применяем таблицу преобразования Лапласа и свойство линейности. Тогда Лаплас- прообраз функции F(s):
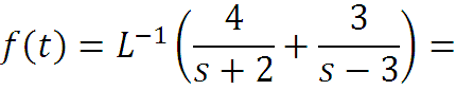
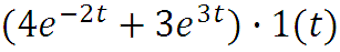
49
6.4.Обратное преобразование Лапласа
-
Преобразование Лапласа от свертки
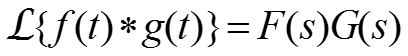
Доказательство:
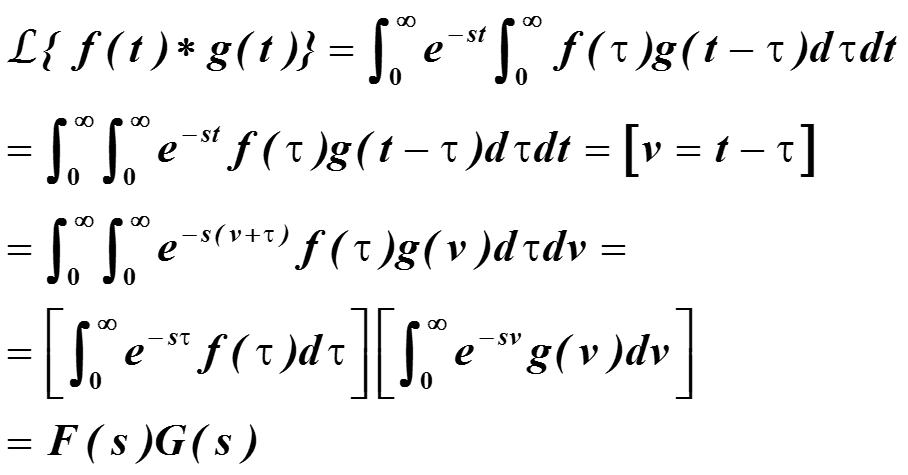
Page 50
6.4.Обратное преобразование Лапласа
-
В частности, для свертки с импульсом получается:
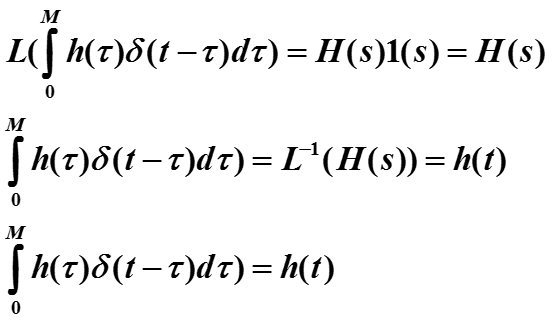
Еще раз получено свойство фильтрации δ - функции!
-
Обратное преобразование от произведения функций равно свертке их прообразов :
-
L-1(F(s) G(s)) = f(t)*g(t)
-
Прямое преобразование от произведения функций равно свертке их образов с коэффициентом:
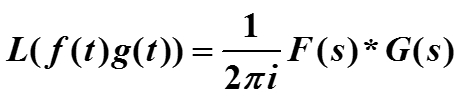
Page 51
6.4.Обратное преобразование Лапласа
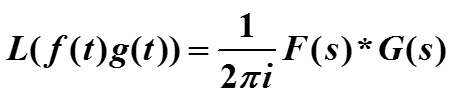
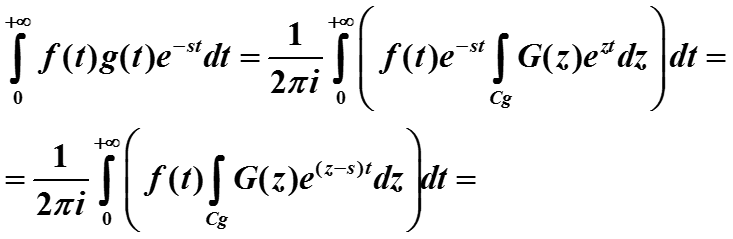
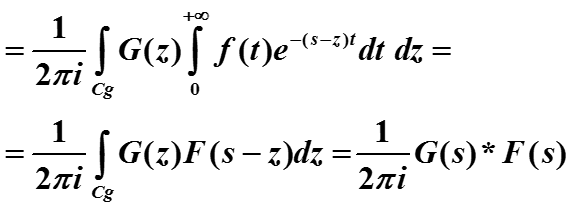
Page 52
6.5. Непрерывные и дискретные преобразования
-
Для обработки аналоговых (непрерывных) сигналов существует математический аппарат, включающий преобразования Фурье, Лапласа, вейвлеты и др. Обработка цифровых сигналов есть не что иное, как обработка последовательностей (дискретных, может быть и квантованных, значений сигнала). Прямое применение интегральных преобразований к дискретным сигналам затруднительно, хотя и возможно.
-
Для дискретных сигналов на основе непрерывных преобразований строятся дискретные преобразования, например, дискретное преобразование Фурье.
53
6.5. Непрерывные и дискретные преобразования
-
Кратко рассмотрим z-преобразование, которое является в некотором смысле, аналогом преобразования Лапласа для дискретных сигналов, выраженных как последователь-ности значения сигнала в дискретные моменты времени.
-
Сигналы передаются двумя способами: 1) по проводящему кабелю; 2) в эфире (беспроводная связь).
-
В обоих случаях на физическом уровне передается аналоговый сигнал. Передающая сторона использует дискретный (цифровой) сигнал, но передающая аппаратура в любом случае на выходе генерирует аналоговый сигнал. Для выделения из него дискретного сигнала принимающая сторона применяет модем или другое устройство, распознающее пороговые значения.
54
6.5. Непрерывные и дискретные преобразования