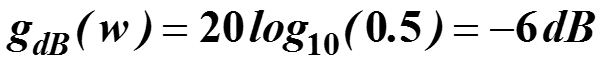Преобразование Лапласа. Решение дифференциальных уравнений преобразованием Лапласа. Обратное преобразование Лапласа, страница 7

Таблица z-преобразования (2)

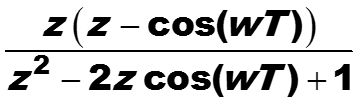
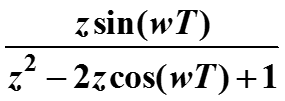
78

6.7. Свойства z-преобразования

Таблица z-преобразования (3)

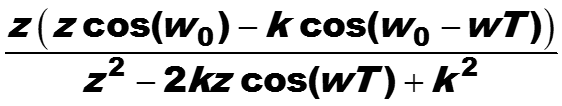
где

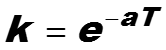
79

6.8. Обратное z-преобразование

• z-преобразование является аналогом преобразования Ла-пласа. Обратное z-преобразование вычисляется по фор-муле, похожей на формулу обратного преобразования Лапласа.
• Интегральное преобразование

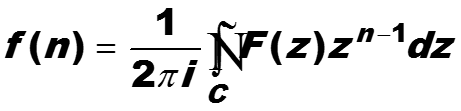
• определенное для всех целых чисел n называется обрат-ным z-преобразованием. С – замкнутый контур, включа-ющий все полюсы функции F(z) или прямая z = C, где С – вещественное число, по модулю бОльшее модулей всех полюсов функции F(z) .

80

6.8. Обратное z-преобразование

• При инженерном использовании z- преобразования обратное преобразование находят по таблицам, не применяя интегрирование.
• Для рациональных функций обратное z-преобразование вычисляют разложением рационального выражения на сумму элементарных дробей. При этом вместо дробей вида

• Применяют дроби вида

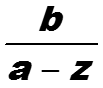
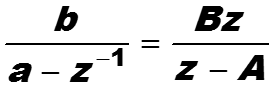
81

6.9. Анализ и проектирование фильтров

• При проектировании фильтра цифрового сигнала во-пер-вых учитывается рассматриваемый диапазон частот. Если следует принимать во внимание частоты до wf рад/с, то по критерию Найквиста (Т Котельникова) период дискре-тизации сигнала T должен быть не более, чем

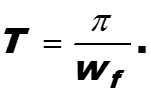
• Если выбран период дискретизации Т, то учитываются все интервалы времени, на которых период сигнала >= T. Основное назначение фильтра – усиление входного сигнала в зависимости от диапазона частоты. Для решения этой задачи фильтр исследуется в частотной области. Если речь идет о цифровых сигналах, то разумно применять z-преобразование.

82

6.9. Анализ и проектирование фильтров

• Для оценки воздействия фильтра на входной сигнал используется понятие усиления сигнала. Усилением (коэффициентом усиления) сигнала на частоте w называется отношение

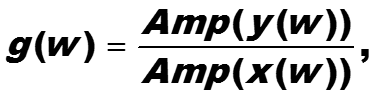
• где Amp(x(w)) , Amp(y(w)) – максимальные модули амплитуд входного и выходного синусоидальных сигналов на частоте w.
• В отличие от других задач теории сигналов, при анализе и проектировании фильтров рассматривают 1) только си-нусоидальные сигналы; 2) для этих сигналов принимают во внимание только амплитуды. В других задачах самыми важными характеристиками могут быть фазы сигналов.

83

6.9. Анализ и проектирование фильтров

• Реальный фильтр не просто умножает амплитуду вход-ного сигнала на коэффициент усиления. На некоторых частотах могут наблюдаться провалы сигнала или чрезмерное усиление.
• В теории сигналов коэффициент усиления выражается в децибеллах

• такая логарифмическая шкала получена эксперименталь-ным путем. Например,

84

6.9. Анализ и проектирование фильтров

• Пример анализа усиления сигнала.
• Пусть выходной сигнал задан соотношением

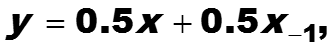
• Найти коэффициент усиления сигнала в диапазоне [200, 600 рад/с] = [32, 96.5 Hz] .
• Решение. Запишем уравнение в более удобном виде

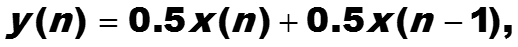
• Применим к обеим частям z-преобразование. Тогда по свойству сдвига

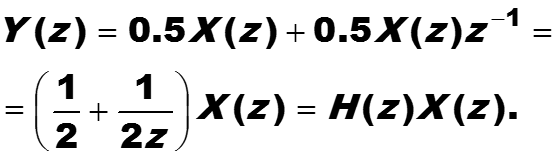
85

6.9. Анализ и проектирование фильтров

• Оператор

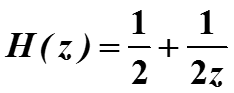
• преобразует входной сигнал в выходной. Он и обеспечи-вает усиление сигнала.
• Вычислим усиление Z-образа входного сигнала x(n) , представленного синусоидой x(n) = sin(n) 1(n). По ранее полученному результату

• То есть

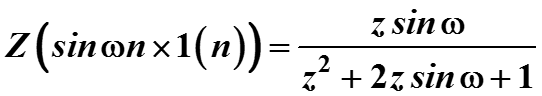
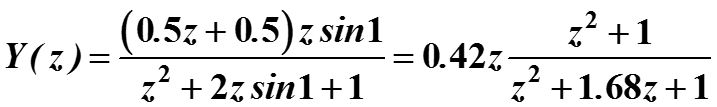
86

6.9. Анализ и проектирование фильтров

• Графики Z-образов входного и выходного сигналов

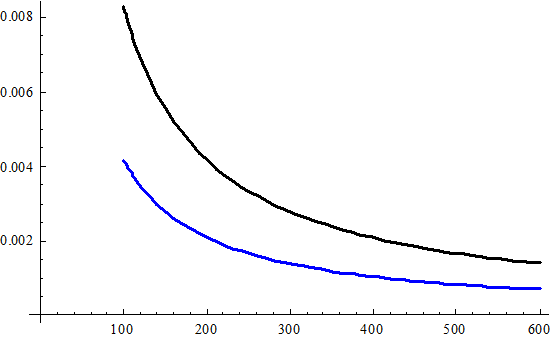
• (Выше X(z) - черный, ниже Y(z) – синий)
• Фильтр уменьшил амплитуду частоты сигнала в 2 раза, то есть, коэффициент усиления в диапазоне [200, 600 рад/с] равен

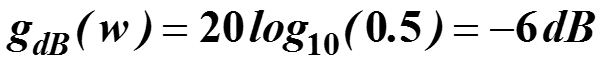
87

6.9. Анализ и проектирование фильтров

• На самом деле коэффициенты усиления вычисляются немного другим способом.
• Коэффициенты усиления определены не для времени, а для амплитуд частот. Для вычисления модуля передаточной функции
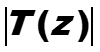
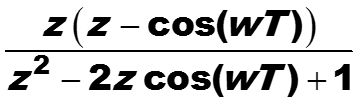
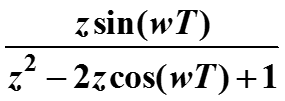
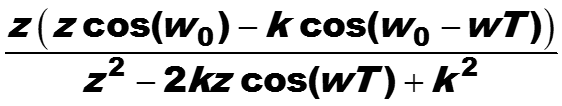
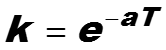
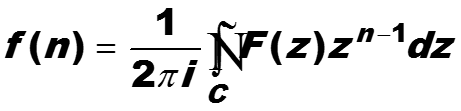
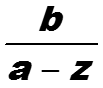
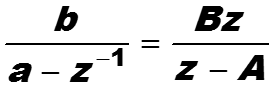
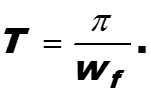
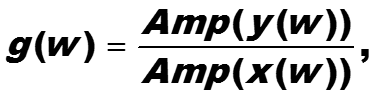
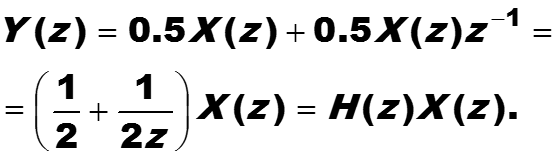
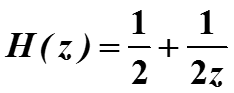
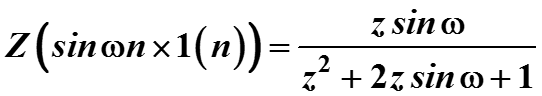
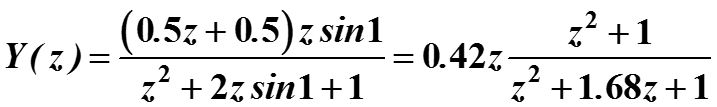