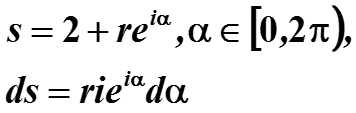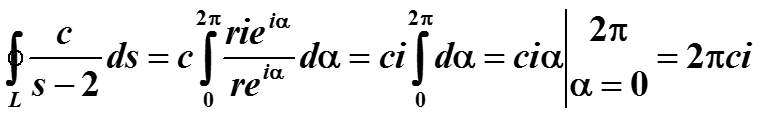-
Пусть ω =1, y(0) = y’(0)=1, r(t) = sin 2t.
-
Тогда
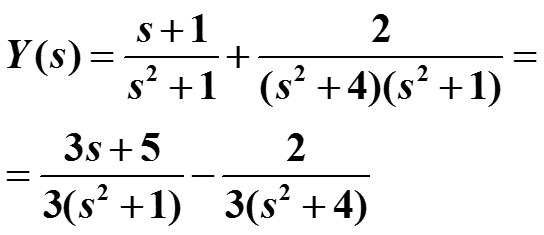
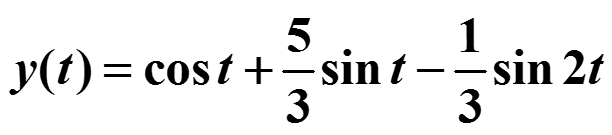
32
6.3.Решение диф. уравнений преобразованием Лапласа
-
Графики входного и выходного сигналов :
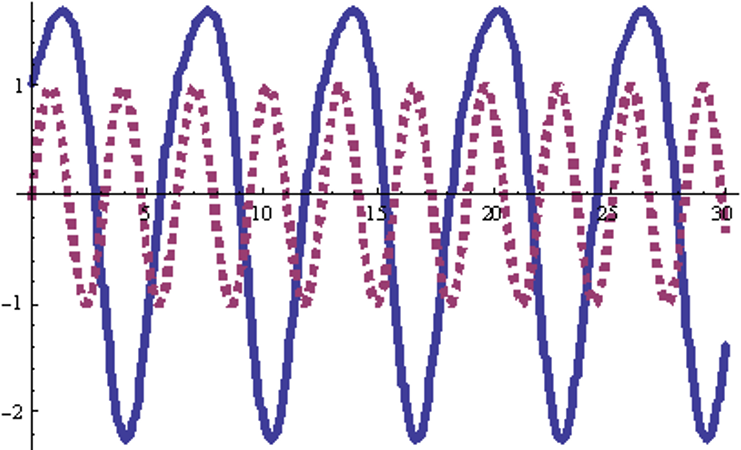
33
6.4.Обратное преобразование Лапласа
-
Преобразования Лапласа содержит интеграл с пределами интегрирования от 0 до +∞. Будем предполагать, что для t < 0 функция f(t) = 0.
-
Обратным преобразованием Лапласа функции F(s) называется интегральное преобразование
-
где путь интегрирования идет вдоль прямой линии
-
C: Re s = c, c = const
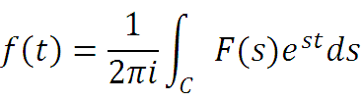
34
6.4.Обратное преобразование Лапласа
-
Определим обратное преобразование Лапласа функции F(s) как прообраз прямого преобразования.
-
Это означает, что обратное преобразование вычисляется по таблице прямого преобразования. При этом можно использовать свойства преобразования, что расширяет множество спектральных функций, для которых мы можем найти обратное преобразование.
-
При этом возникает вопрос существования и единственности Лаплас-прообраза. Мы не рассматриваем эти вопросы.
-
Более правильный подход состоит в построении обратного преобразования по аналогии с преобразованием Фурье, где мы определяли и прямое и обратное преобразования через , , интеграл Фурье.
35
6.4.Обратное преобразование Лапласа
-
Прямая линии Re s = c, c = const на комплексной плоскости имеет график
Im s
Re s
0
с
-
Вспомним интегрирование комплексной функции по контуру (контур проходим против часовой стрелки)
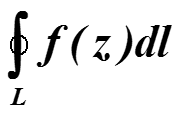
36
6.4.Обратное преобразование Лапласа
-
Интегрирование по прямой Re s = c на комплексной плоскости можно представить как предельный случай интегрирования по контурам, представляющим собой окружности, касающиеся прямой
-
При увеличении радиуса окружность приближается к прямой.
37
6.4.Обратное преобразование Лапласа
-
Интегрирование по контурам выполняется в положительном направ-лении, то есть против часовой стрелки. Если расположить окружно-сти справа от прямой, то соответственно интегрирование по
Im s
Re s
0
с предельной прямой будет выполняться в противоположном направле-нии, значение интеграла будет другим.
38
6.4.Обратное преобразование Лапласа
-
Вспоминаем высшую математику
-
1) Если контур замкнут и комплексная функция f(z), z=x+iy имеет производные всех порядков по x, по у и смешанные производные (такая функция называется аналитической), то
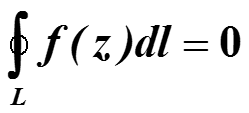
y
L
x
0
39
6.4.Обратное преобразование Лапласа
-
Вспоминаем высшую математику
-
2) Если комплексная функция f(z) имеет все эти производные во всех точках внутри контура, кроме точки z0=(x0, y0) то
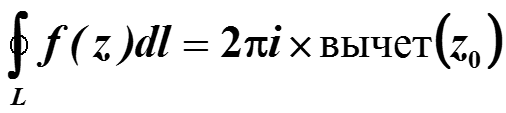
y
L
z
x
0
40
6.4.Обратное преобразование Лапласа
-
Вспоминаем высшую математику
-
Теорема Коши. Если и g(z) – аналитическая
-
функция, то вычет в точке a = x0 + iy0 равен g(a), то
-
есть интеграл
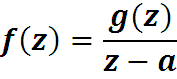
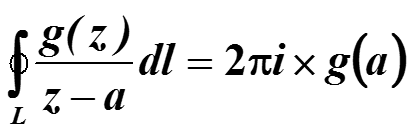
y
L
z0
x
0
41
6.4.Обратное преобразование Лапласа
Пример. Найти интеграл по окружности от комплексной функции
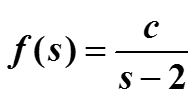
Здесь , т.е. g(2) = c, по теореме Коши интеграл должен быть равен 2πi c.
Проверим это интегрированием. Интегрируем по окружности. Заменяем (s – 2) на точки окружности и интег-рируем, переменная r является контан-той, угол α изменяется от 0 до 2π
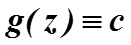

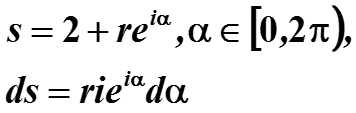
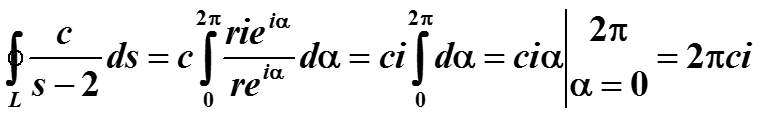
42
6.4.Обратное преобразование Лапласа
-
Существуют 2 способа вычисления обратного преобразования Лапласа :
-
1) вычислять интеграл по прямой линии, лежащей на комплексной плоскости;
-
2) вычислять интеграл как обратный от Лаплас-образа по таблице преобразования Лапласа.
-
Первый способ универсальный, но требует хорошей математической подготовки. Обычно инженер не выходит за рамки некоторого набора распространенных функций и использует таблицу.
6.4.Обратное преобразование Лапласа

6.4.Обратное преобразование Лапласа
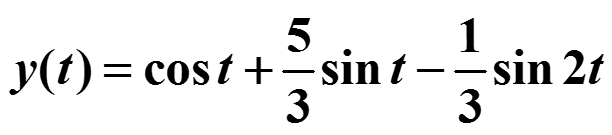

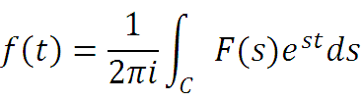
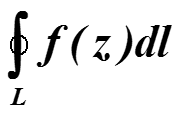
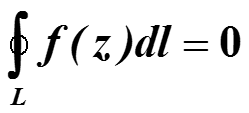
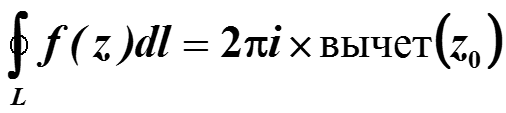
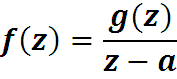
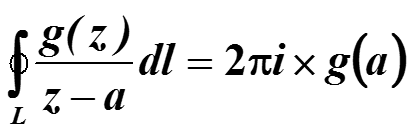
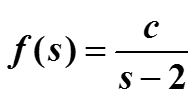
![]()
![]()