-
Проблему потери сигнала при дискретизации решает критерий Найквиста (Теорема Котельникова). Интервал дискретизации T должен быть в 2 или более раз меньше, чем период сигнала, который дискретизируют, то есть на периоде сигнала должно быть как минимум 2 точки дискретизации.
-
Это то же самое, что частота дискретизации должна быть в 2 или более раз больше, чем частота сигнала, который дискретизируют.

55
6.6. Дискретное преобразование Лапласа
-
Если ввести функцию единичного импульса
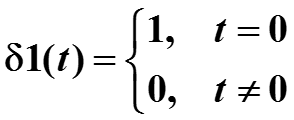
-
то можно записать весь дискретизированный сигнал через сумму импульсных сигналов.
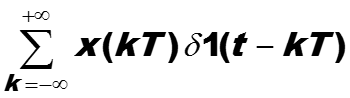
-
Если обозначить x(t) – аналоговый сигнал, а x*(t) его дискретизация с интервалом T, то
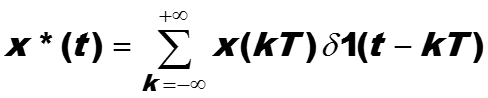
56
6.6. Дискретное преобразование Лапласа
-
В частности, дискретизированная функция Хевисайда представляется в виде
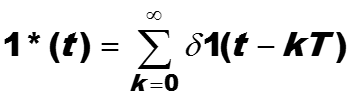
-
Если сигнал f(t) задан для неотрицательного аргумента t, то считая его равным нулю для отрицательных t, дискретизированный сигнал f*(t) можно записать так:
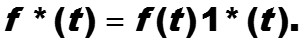
-
Построим преобразование Лапласа от сигнала f*(t) :
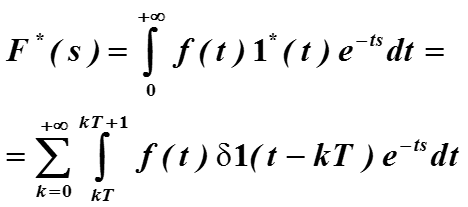
57
6.6. Дискретное преобразование Лапласа
-
По свойству фильтрации элемент ряда равен
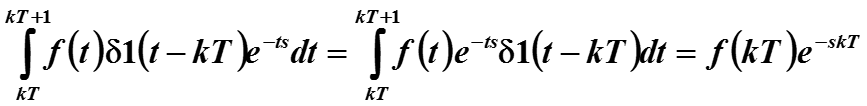
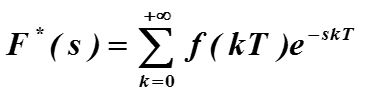
-
Для проверки сходимости ряда, используются признаки сходимости функциональных рядов. Формально заменим переменную s на новую переменную
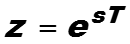
-
Тогда Лаплас-образ дискретизированного сигнала f*(t) будет равен
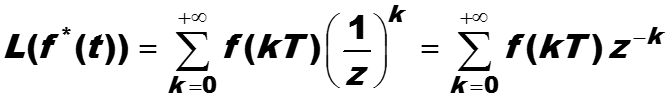
58
6.6. Дискретное преобразование Лапласа
-
Из преобразование Лапласа получено дискретное преобразование для дискретного сигнала. Переменная дискретного времени kT перешла в частотную непрерыв-ную переменную s, а затем в новую частотную непрерыв-ную переменную z.
-
Построенное преобразование отличается от z-преобразо-вания областью индекса суммирования, для z-преобразо-вания индекс принимает целые значения от минус до плюс бесконечности, для построенного преобразования суммирование выполняется только от нуля до плюс бесконечности.
-
Тем не менее преобразования совпадают для сигналов f(t), которые обращаются в нуль для отрицательных от-счетов времени (значения сигнала f(t) до начала отсчета t=0 не учитываются).
59
6.6. z-преобразование
-
Для объекта с дискретным входным сигналом x(t) и дискретным выходным y(t) сигнал y(n) в момент времени n можно задавать в зависимости от значений входного сигнала x в предыдущие моменты времени, включая и момент n. Кроме того, выходной сигнал y может зависеть от своих значений в предыдущие моменты времени (обратная связь).
-
Принято обозначать текущий дискретный момент времени через индекс 0, а предыдущие моменты времени индексами -1,-2,-3, …. Тогда

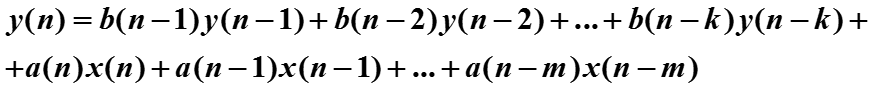
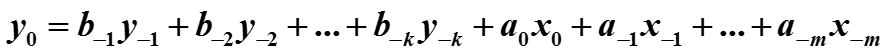
60
-
Здесь a и b – числовые коэффициенты.
6.6. z-преобразование
-
По этой формуле можно вычислить значение выходного сигнала y в момент времени n, зная значения
-
1) y на k предыдущих моментах;
-
2) входного сигнала x на текущем и на m предыдущих моментах.
-
Уравнение предыдущего слайда называются уравнением в конечных разностях или разностным уравнением. По таким уравнениям нетрудно построить аппаратную реализацию объекта выходного сигнала, но трудно получить выражение для выходного сигнала в явном виде, что бывает необходимым во многих случаях, например, чтобы провести анализ объекта.

61
6.6. z-преобразование
-
Дифференциальные уравнения и разностные уравнения – близкие понятия. Если взять разность двух последовательных значений сигнала x(t) в моменты 0 и -1 и разделить на интервал ∆ между этими моментами, то по определению производной получим приближенное значение производной в точке 0 :
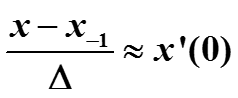

-
Это же соотношение можно записать иначе :
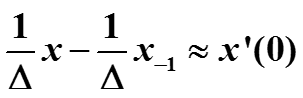
62
6.6. z-преобразование
-
Вторую производную в точке 0 можно приближенно вычислить как производную от приближенной первой производной :
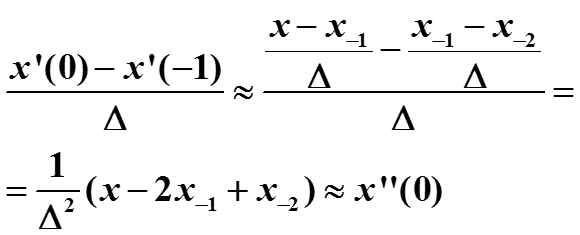


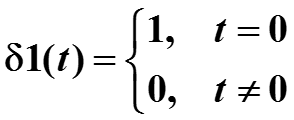
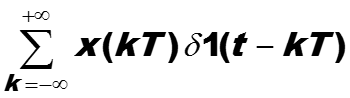
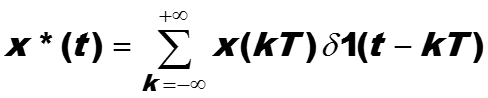
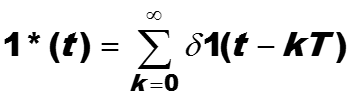
![]()
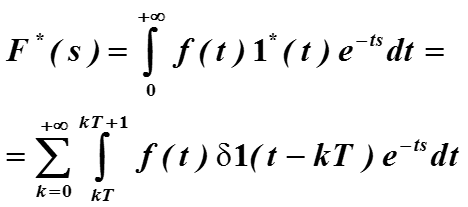
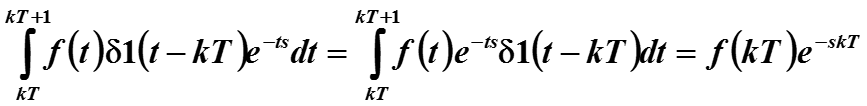
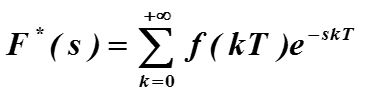
![]()
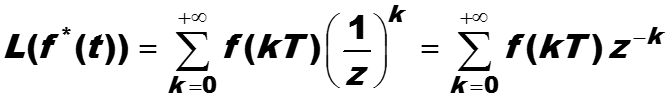
![]()
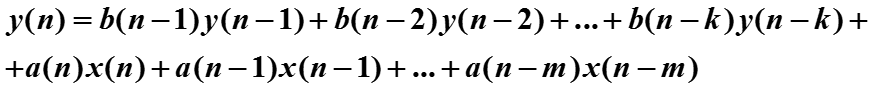
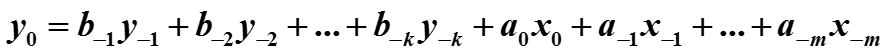
![]()
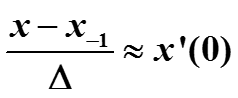
![]()
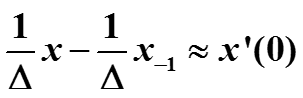
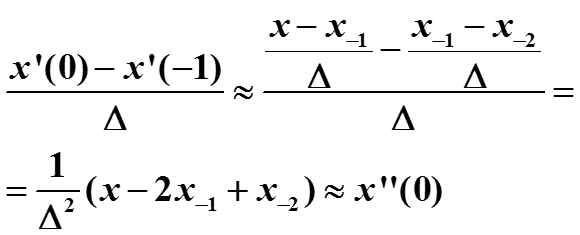
![]()