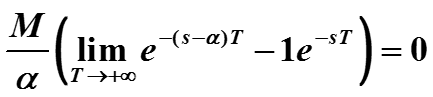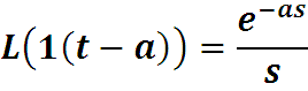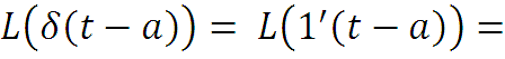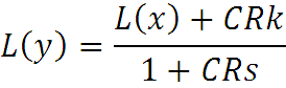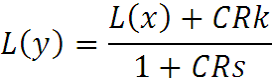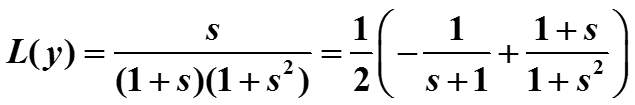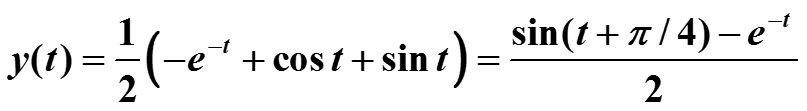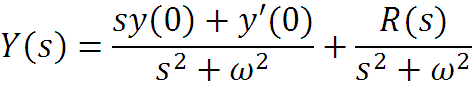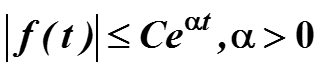
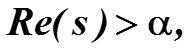
Математика \ Основы теории управления и системотехники

Преобразование Лапласа. Решение дифференциальных уравнений преобразованием Лапласа. Обратное преобразование Лапласа, страница 2

и то

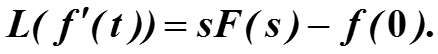
19

6.2. Преобраание Лапласа

4. Преобразование интеграла: если для некоторого вещественного α>0 функция f(t) ограничена экспонентой:

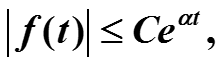
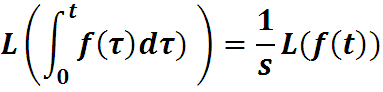
то

  • Доказательство свойств преобразования Лапласа.
  • Свойство 1 очевидно.
  • Свойство 2 доказывается заменой переменных, доказать самостоятельно.
  • Докажем свойство 3 (дифференциальное свойство).

20

6.2. Преобразование Лапласа

  • Доказательство дифференциального свойства (свойство 3).
  • Определим две положительные величины

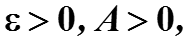
и запишем преобразование Лапласа производной через пределы

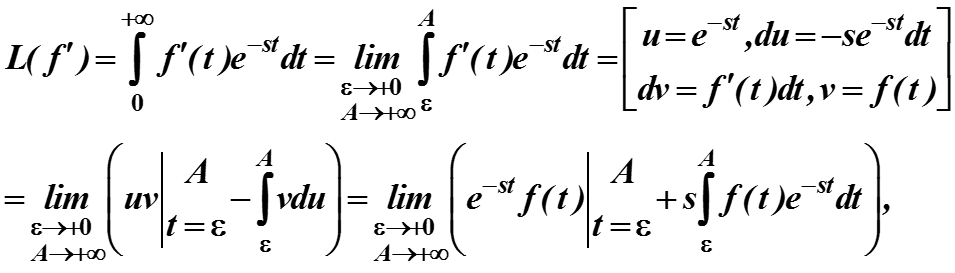
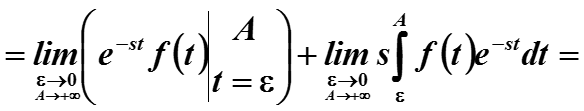
= Слагаемое I + Слагаемое II

21

6.2. Преобразование Лапласа

  • Вычислим Cлагаемое I :

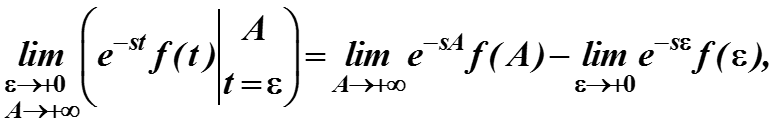
для первого выражения используем ограничение из начального условия

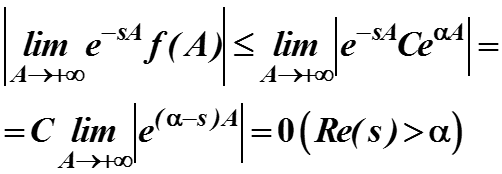
Для второго предел очевидно равен

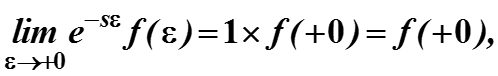
Если f(t) непрерывна, то этот предел равен просто f(0).

6.2. Преобразование Лапласа

  • Окончательно Cлагаемое I равно :

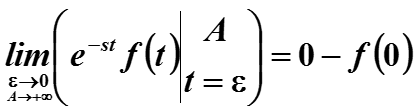
  • Cлагаемое II вычисляется простым переходом к пределу :

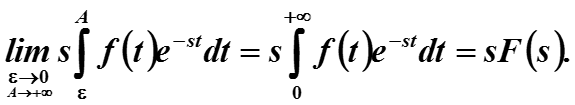
Таким образом, получено дифференциальное свойство преобразования Лапласа

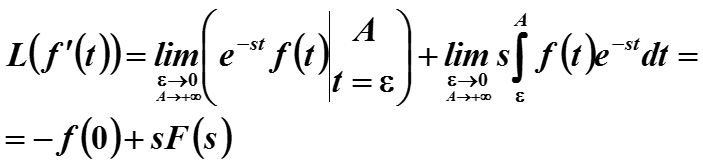
6.2. Преобразование Лапласа

  • Используя дифференциальное свойство можно найти преобразова-ние Лапласа от второй производной сигнала.
  • Выводим f’’(t) = (f’(t))’. Исходным сигналом считаем f’(t), запишем для него дифференциальное свойство

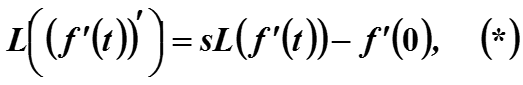
  • По дифференциальному свойству

  • Подставляя это равенство в (*), получаем

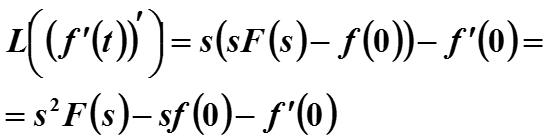
  • Таким же способом можно получить формулы преобразования Лапласа для старших производных.
  • Но следует помнить, что для разрывных в точке 0 функций нужно брать f(+0) и f’(+0) (предел слева) вместо f(0) и f’(0) .

6.2. Преобразование Лапласа

  • Доказательство интегрального свойства (свойство 4)

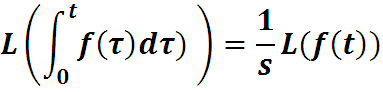
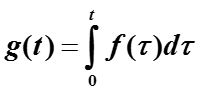
Тогда

Определим функцию g(t) :

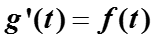
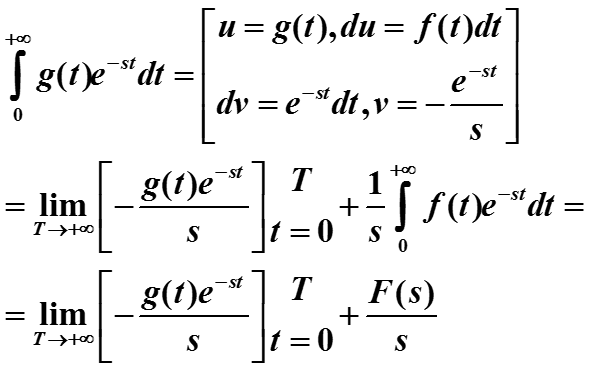
25

6.2. Преобразование Лапласа

Значение нижней подстановки равно 0, так как

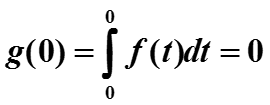
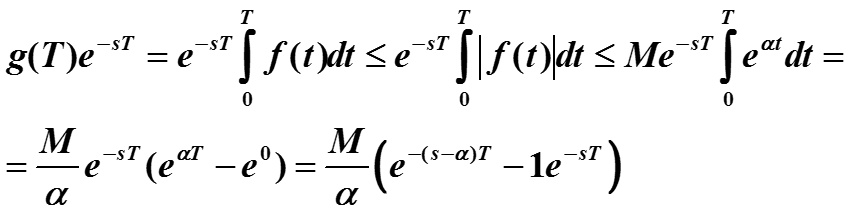
(иначе интеграл расходится и преобразования Лапласа не существует) поэтому

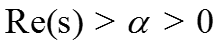
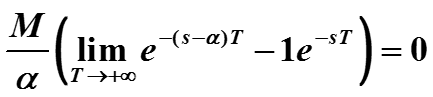
26

6.2. Преобразование Лапласа

  • Применение свойств для вычисления преобразования Лапласа.
  • Применяя свойство 3 найдем преобразование Лапласа для дельта-функции δ(t - a), (а > 0). Эта функция является производной от функции Хевисайда 1(t - a), мы показали, что
  • Тогда по свойству 3

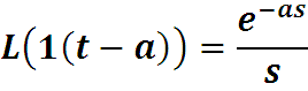
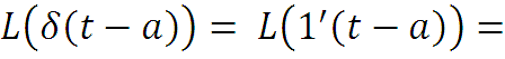
  • Упражнение. Найти преобразование Лапласа для дельта-функции δ(t + a), (а > 0).

27

6.3. Решение диф. уравнений преобразованием Лапласа

  • Применение преобразования Лапласа к дифференциальному уравнению RC-цепи.
  • x(t) = С*R * y′(t) + y(t)
  • Применим преобразование Лапласа к обеим частям уравнения. По свойству линейности получаем:
  • L(x(t)) = СR L(y′(t)) + L(y(t))
  • По свойству 3 (преобразование производной) :
  • L(x) = СR (sL(y)-y(0)) + L(y), пусть начальное условие: y(0) = k.
  • Отсюда L(x) = L(y)(1+CRs) – CRk
  • То есть

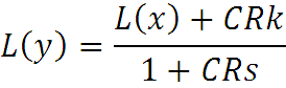
28

6.3.Решение диф. уравнений преобразованием Лапласа

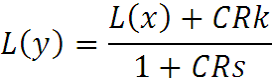
  • Если задана функция x(t), то это выражение дает решение исходного дифференциального уравнения (но это Лаплас–образ решения!).
  • Преобразование Лапласа дифференциального уравнения привело к простому алгебраическому уравнению. Теперь нужно вернуться к исходной переменной t, то есть требуется провести обратное преобразование.
  • Пусть CR=1, x(t) = cos t, k=y(0) = 0. Тогда

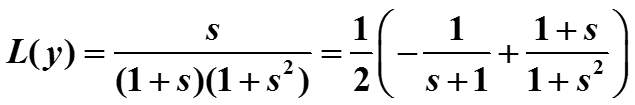
29

6.3.Решение диф. уравнений преобразованием Лапласа

  • Применяя таблицу преобразования Лапласа, получаем

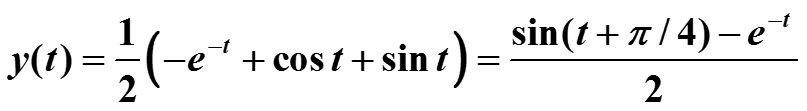
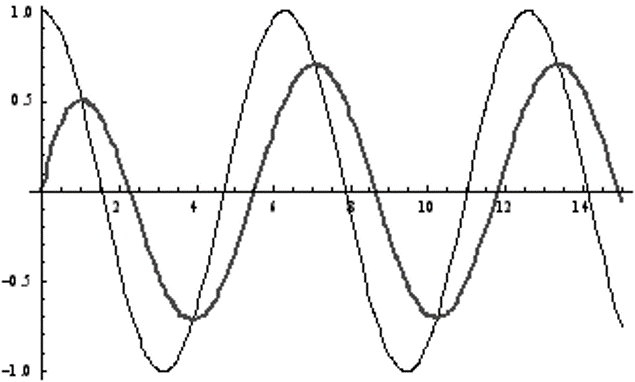
30

6.3.Решение диф. уравнений преобразованием Лапласа

  • Пример. Применение преобразования Лапласа к дифференциальному уравнению колебания :
  • y′′(t) + ω2y(t) = r(t)
  • Дважды применяя свойство преобразования производной, получаем
  • s2 Y(s) – sy(0) – y′(0) + ω2Y(s) = R(s),
  • где Y и R обозначают Лаплас-образы соответствующих функций.
  • Решая полученное алгебраическое уравнение, получаем

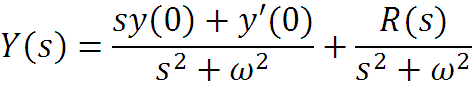
31

6.3.Решение диф. уравнений преобразованием Лапласа

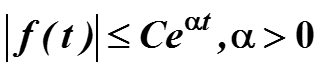
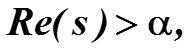
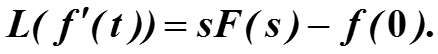
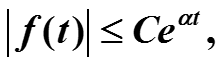
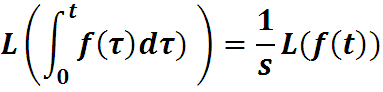
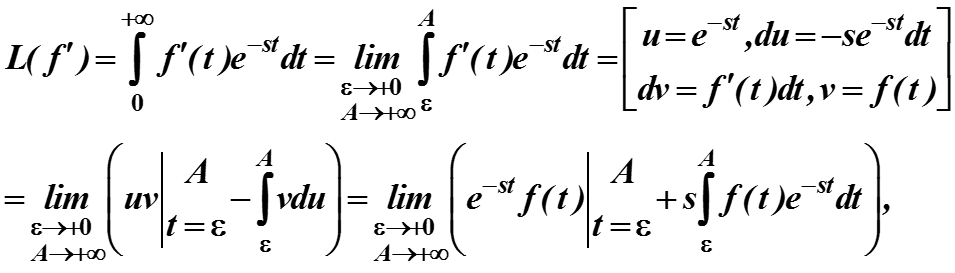
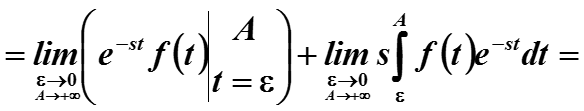
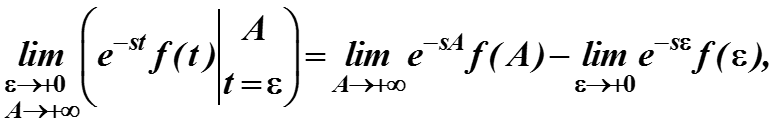
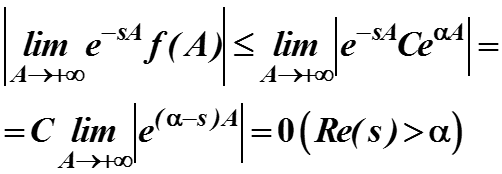
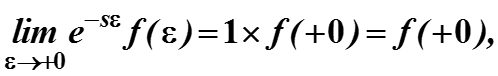
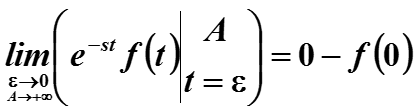
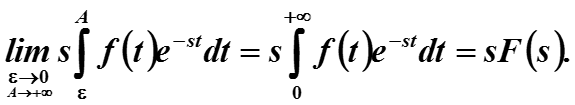
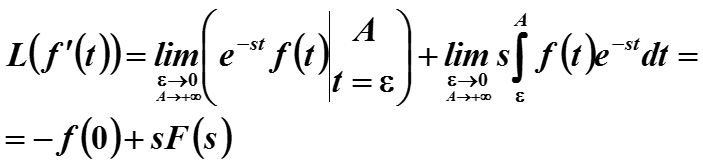
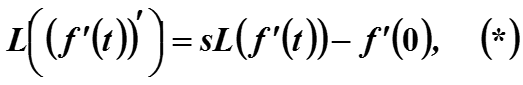
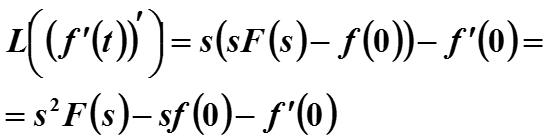
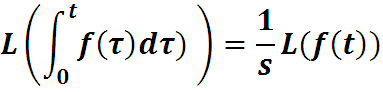
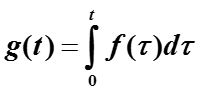
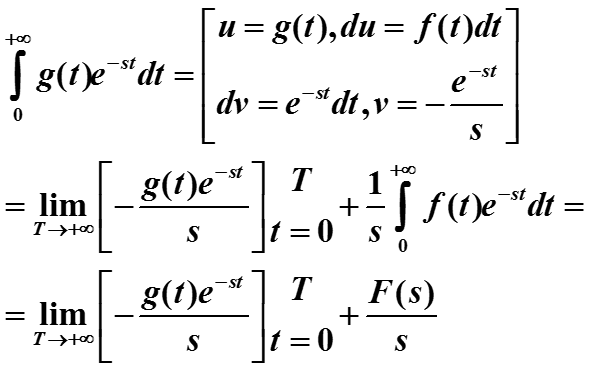
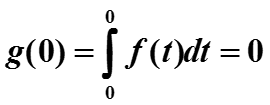
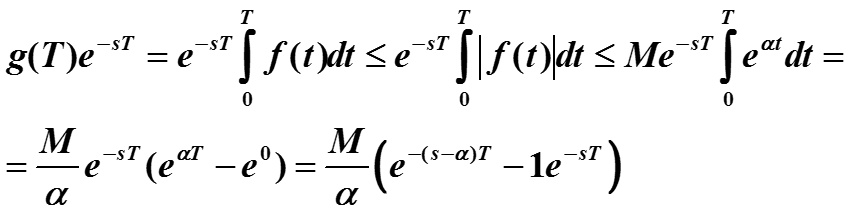
Скачать файл