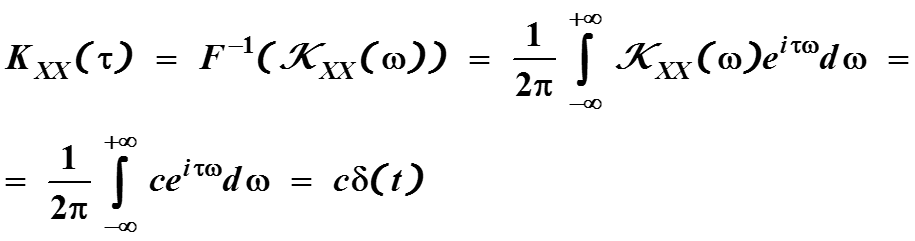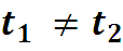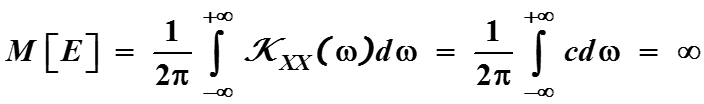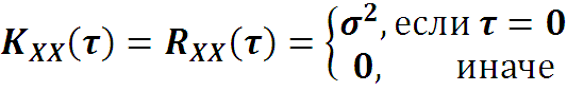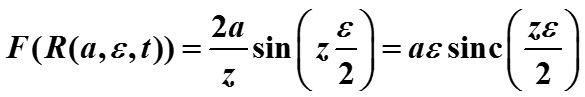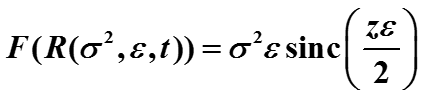Белый шум. Гауссовский белый шум. Физические источники белого шума

9. Белый шум

Page 1

9. Белый шум

Page 2

9.1. Определение белого шума

Стационарный в узком смысле случайный процесс с функ-цией спектральной плотности мощности, равной положи-тельной постоянной величине, называется белым шумом.
Название произошло из оптики, белый цвет получается смешиванием волн различных частот видимого диапазона.
Обычно в процессе белого шума математическое ожидание равно нулю, m = 0.
Так как белый шум стационарный в узком смысле процесс то его автокорреляционная функция зависит от одного аргумента τ;
KXX(τ) является четной.

Page 3

9.1. Определение белого шума

Функция спектральной плотности KXX(ω) получается из автокорреляционной функции преобразованием Фурье, а поскольку функция KXX(ω) четная, то можно использо-вать косинус-преобразование.
Пусть KXX(ω) = c > 0. Обратное преобразование Фурье (или обратное косинус-преобразование) постоянной функции равно δ-функции с коэффициентом c

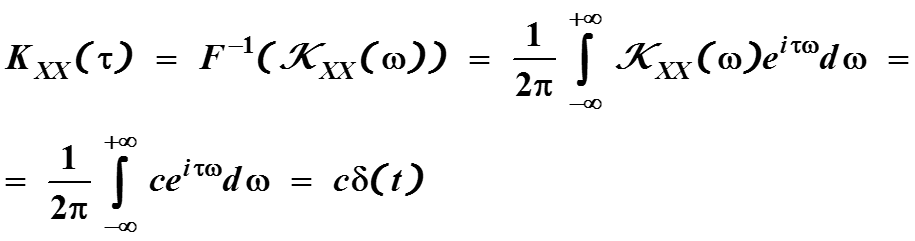
Page 4

9.1. Определение белого шума

Следовательно, белый шум – некоррелированный процесс, случайные величины X(t1) и X(t2) , то есть их корреляция равна нулю (сл. величины линейно независимы) для любых . Распределение случайной величины X(t0) в определении белого шума не уточняется, оно может быть любым.
Энергия сигнала пропорциональна интегралу
Отсюда следует, что белого шума не существует.

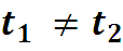
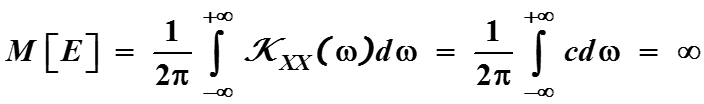
Page 5

9.2. Гауссовский белый шум

Рассмотрим стационарный некоррелированный гауссовский процесс.
Пусть математическое ожидание процесса a = 0, средне-квадратическое равно σ. Тогда ввиду нулевого математи-ческого ожидания

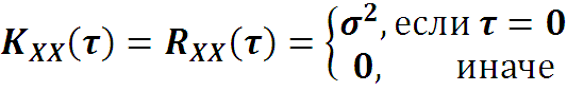
Если σ стремится к бесконечности, то такой гауссовский процесс стремится к белому шуму. Но в реальном при-ложении приходится ограничиться конкретным значени-ем среднеквадратического σ . Положим σ = 10 , и найдем спектральную плотность такого процесса.

Page 6

9.2. Гауссовский белый шум

Найти преобразование Фурье функции KXX(τ) гауссовского процесса можно предельным переходом (при ε стремится к 0) преобразования Фурье прямоугольного импульса R(σ2, ε, t) (см. 3.8. Примеры Фурье-преобразований).

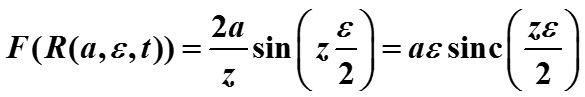
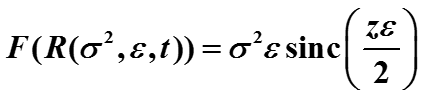
В правой части получена функция, которая при ε 0 стремится к спектральной функции плотности KXX(ω) белого шума.

Page 7

9.2. Гауссовский белый шум

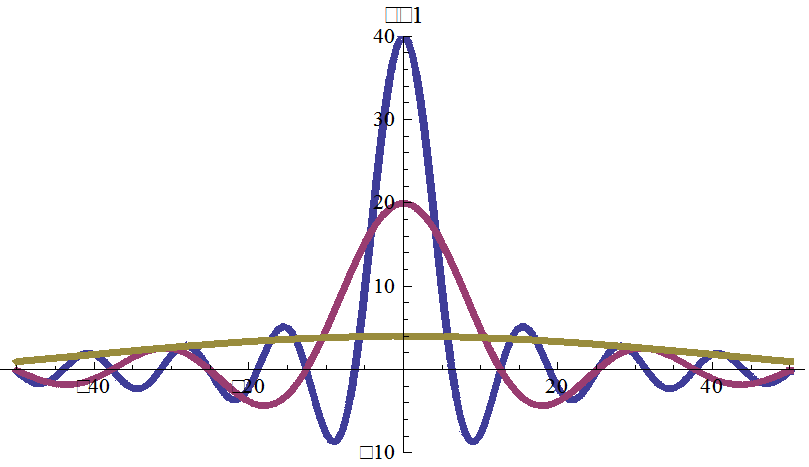
Графики приближения спектральной плотности, полученной из гауссовского процесса при σ = 10
для ε = 1, 0.5, 0.1

Page 8

9.2. Гауссовский белый шум

Функция действительно стремится к постоянной, но эта постоянная равна нулю. Тем не менее на ограниченном интервале частот функцию приближенно можно считать ненулевой постоянной.
Таким образом, стационарный некоррелированный гаус-совский процесс можно рассматривать как приближение к белому шуму. Это реально используется в практических задачах.

Page 9

9.2. Гауссовский белый шум

Применяя свойство эргодичности гауссовского процесса, оценим функции автокорреляции и спектральной плотности по одной реализации объемом n=1000 измерений.
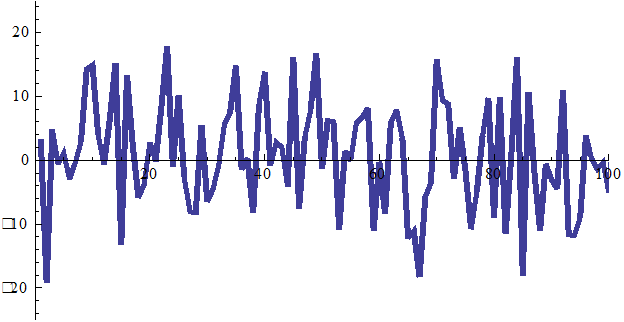
График реализации некоррелированного гауссовского процесса при a = 0, σ = 10.

Page 10

9.2. Гауссовский белый шум

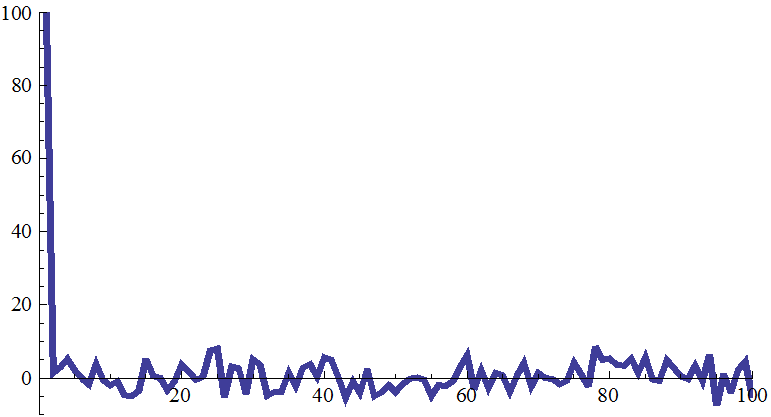
График оценки функции автокорреляции (статистическая функция автокорреляции ) при n=1000 , a = 0, σ = 10.

Page 11

9.2. Гауссовский белый шум

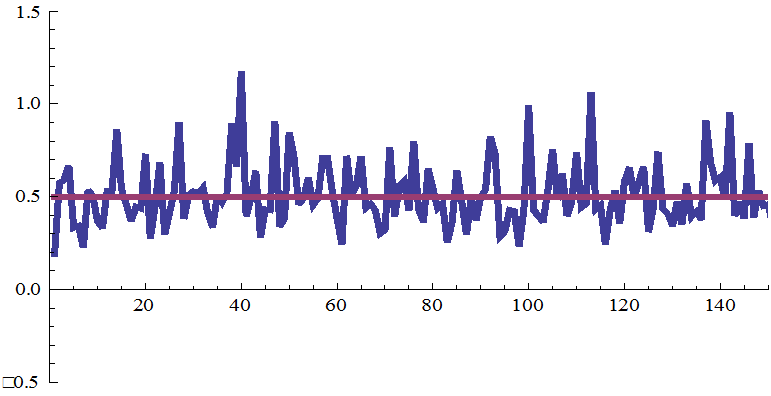
График статистической функции спектральной плотности при n=1000 , a = 0, σ = 10 (интеграл вычислялся методом прямоугольников, красная горизонтальная прямая – среднее значение функции)

Page 12

9.2. Гауссовский белый шум

В качестве приближения к белому шуму можно выбирать любой некоррелированный стационарный (достаточно в узком смысле) процесс. Например, можно взять дискретный процесс D(t) с двумя равновероятными состояниями +1 и -1, в моменты t = 0, 1, 2, … процесс принимает одно из этих состояний. (Одна неприятность : если вычислить корреляцию совместного распределения двух таких величин, то окажется, что она не равна нулю).
Упражнение. Найти корреляцию совместного распред., характеристики процесса D(t) (математическое ожидание, дисперсию, автокорреляционную функцию, функцию спектральной плотности).

Page 13

9.3. Физические источники белого шума