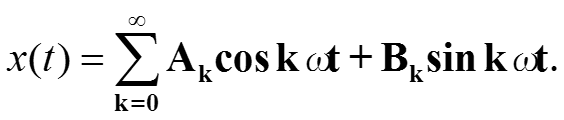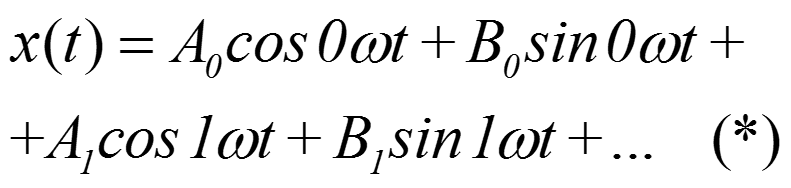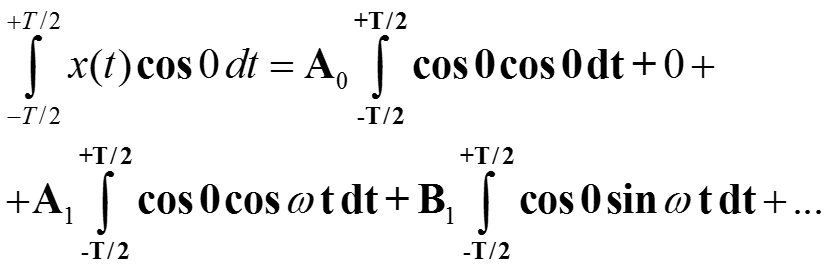Преобразование Фурье. Базисные функции ряда Фурье. Коэффициенты разложения в ряд Фурье

3. Преобразование Фурье

1

Преобразование Фурье

3.1. Базисные функции ряда Фурье. 3.2. Коэффициенты разложения в ряд Фурье. 3.3.Временная и частотные области сигнала. 3.4. Комплексная форма ряда Фурье. 3.5. Интеграл Фурье. 3.6. Преобразование Фурье. 3.7. Синус- и косинус-преобразования.

Page 2

Преобразование Фурье

3.12. Равенство Парсеваля. 3.13. Применение равенства Парсеваля. 3.14. Энергия гармонического осциллятора. 3.15. Приложения преобразования Фурье. 3.16. Таблица преобразований Фурье.

Page 3

3.1. Базисные функции ряда Фурье

• Ряд Фурье и преобразование Фурье – основные инструменты гармонического анализа.
• Ряды Фурье и преобразование Фурье были созданы для изучения распространения тепла в твердых и жидких средах. Фурье исследовал тепловые процессы. Один из опытов был посвящен распространению тепла по железному кольцу. Опыт состоит в следующем. Часть кольца на некоторое время погружается в раскаленные угли. Когда она раскалится докрасна, кольцо вынимают из углей и закапывают в песок. Затем измеряют изменение температуры в точках кольца с течением времени.

Page 4

3.1. Базисные функции ряда Фурье

• График изменения температуры плавно нарастает (в холодной части) и убывает (в раскаленной части) в форме функции синуса. Тепло проходит по кольцу и возвращается в исходную точку (период 2π). Но тепло движется по кольцу в направлении часовой стрелки и противоположном направлении, встречаясь на половине кольца.

Page 5

3.1. Базисные функции ряда Фурье

• В то же время исходная область нагрева не остыла. Получается два источника тепла и период изменения температуры становится равным π. Температура постепенно выравнивается и в конце концов становится одинаковой по всему кольцу.
• Фурье нашел, что первоначальное нерегулярное распределение можно разложить на множество простых синусоид, каждая из которых имеет свой максимум температуры и свою фазу, т.е. свои источники распространения тепла на кольце.

Page 6

3.1. Базисные функции ряда Фурье

• Исходная составляющая один период на кольце (время, за которое тепло проходит полный круг), была названа главной гармоникой, а составляющие с меньшими периодами — соответственно второй, третьей и т.д. гармоникой. Так был построен ряд Фурье.
• Фурье свёл функцию распределения тепла, трудно поддающуюся математическому описанию, к удобным для анализа суммам синусов и косинусов, оказалось, что эти суммы очень точно описывают распределение тепла в твердом теле.

Page 7

3.1. Базисные функции ряда Фурье

• В основе ряда Фурье лежат тригонометрические ортогональные функции.
• Это базисные функции ряда Фурье. Главная гармоника имеет период T, соответственно ω = 2π/T – частота (угловая скорость). Весовая функция s(t) = 1.
• Ортогональность базисных функций разложения означает, что

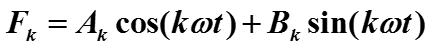
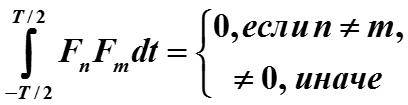
Проверим это свойство интегрированием.

Page 8

3.1. Базисные функции ряда Фурье

• Проверим ортогональность сигналов
• с весовой функцией s(t) = 1 на отрезке t € [-T/2,+T/2]
• T=2π/ω, где m, n – целые числа.
• Найдем скалярное произведение

• Применим формулу

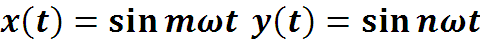
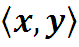
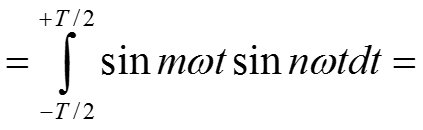
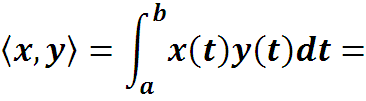
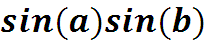
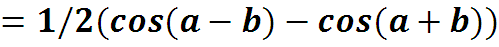
3.1. Базисные функции ряда Фурье

• Если m ≠ n (при интегрировании нужно будет делить на m - n), то

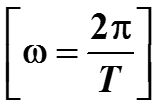
3.1. Базисные функции ряда Фурье

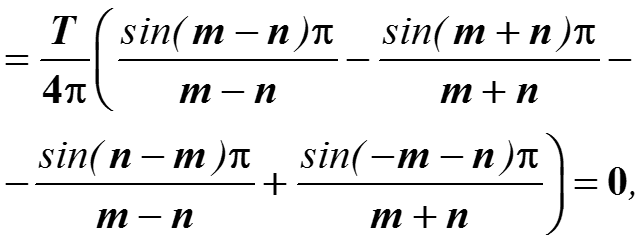
• То есть, для любых целых параметров m ≠ n сигналы ортогональны. При m=n=0 получаем

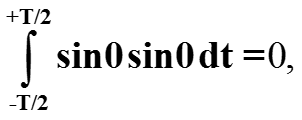
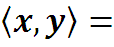
• То есть нулевой сигнал x(t)=0 ортогонален сам себе. (Такой необычный случай желательно исключить).

Page 11

3.1. Базисные функции ряда Фурье

• При m=n ≠0 получаем

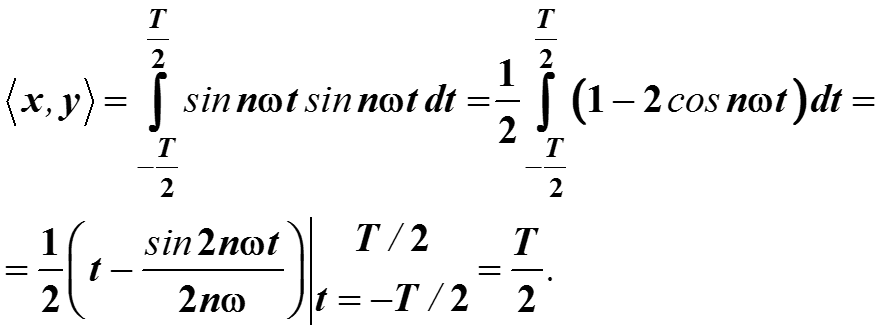
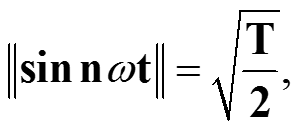
• То есть, норма сигнала sin nωt равна

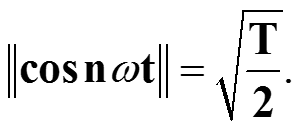
• норма сигнала cos nωt также равна

3.1. Базисные функции ряда Фурье

• Окончательно получаем:
• 1) норма сигнала sin nωt при n=1,2,… равна
• при n=0 норма sin nωt равна 0.
• 2) норма сигнала cos nωt при n=1,2,… также равна
• при n=0 норма cos nωt равна
• Ввиду отличия норм нулевой базисной функции F0 коэффициенты разложения при этой функции имеют особый вид, не соответствующий общей формуле коэффициентов.

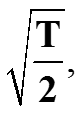
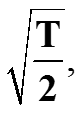
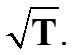
Page 13

3.1. Базисные функции ряда Фурье

• 3) Сигнала sin nωt и sin mωt при n≠m для всех целых n и m ортогональны.
• 4) Сигнала cos nωt и cos mωt при n≠m для всех целых n и m ортогональны (доказать).
• 5) Сигнала sin nωt и cos mωt для всех целых n и m ортогональны (доказано в п. 2.2).
• Исходя их этих результатов легко получить коэффициенты разложения сигнала в ряд Фурье, используя общую формулу коэффициентов разложения в ортогональный ряд.

3.1. Базисные функции ряда Фурье

• Упражнение. Проверить ортогональность сигналов

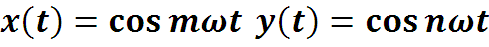
3.2. Коэффициенты разложения в ряд Фурье

• Коэффициенты Ak, Bk ряда Фурье вычисляются с применением свойства ортогональности базисных функций. Общий вид разложения

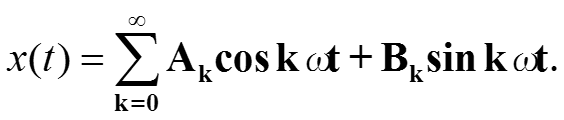
• Вначале найдем коэффициенты A0, B0

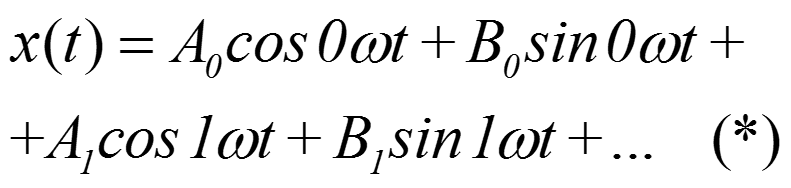
Page 16

3.2. Коэффициенты разложения в ряд Фурье

• Так как sin0 =0, то B0 – любое число, для определенности положим его равным нулю, B0 =0.
• Коэффициент A0 вычислим, умножив обе части (*) на
• cos 0 и интегрируя обе части равенства

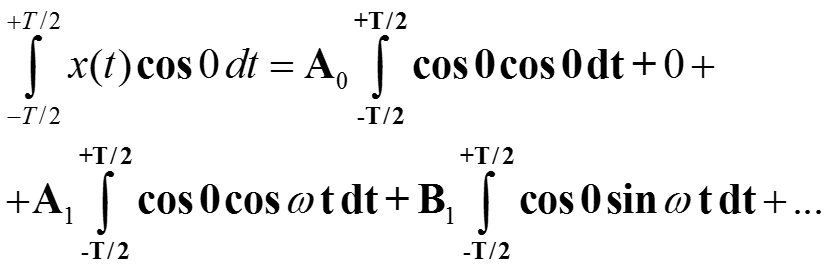
3.2. Коэффициенты разложения в ряд Фурье
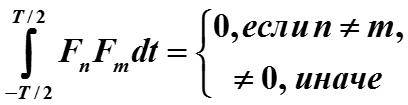
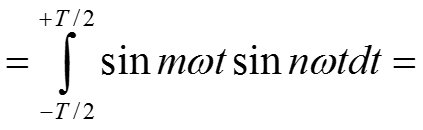
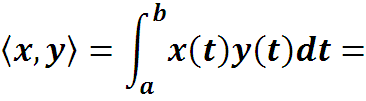
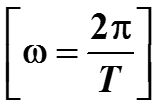
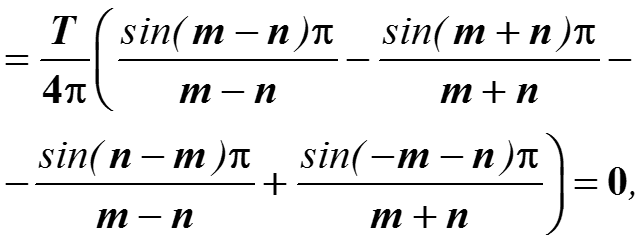
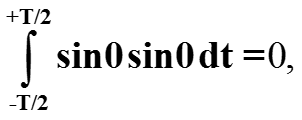
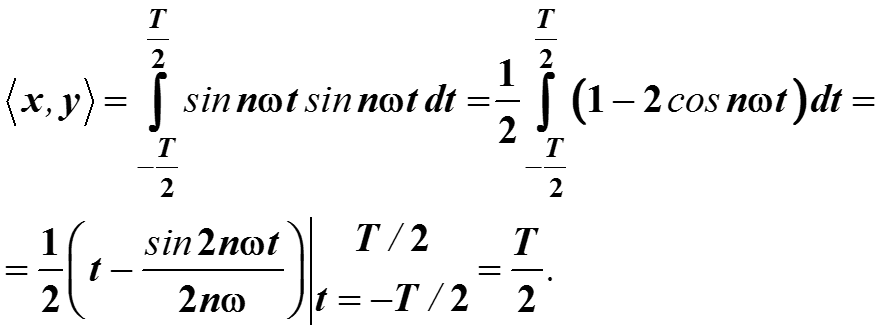
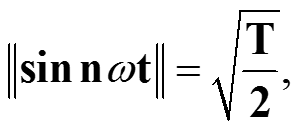
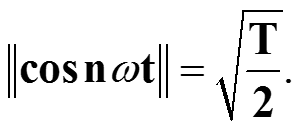
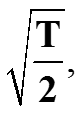
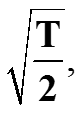