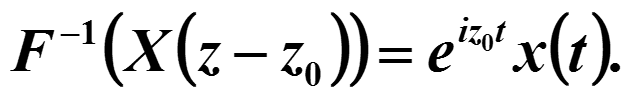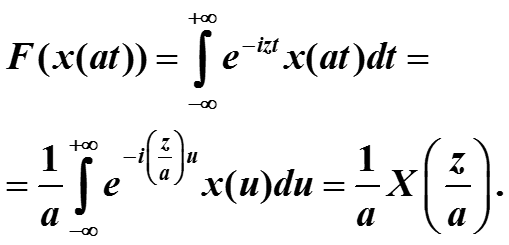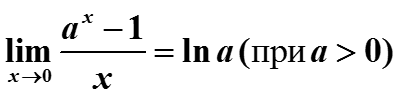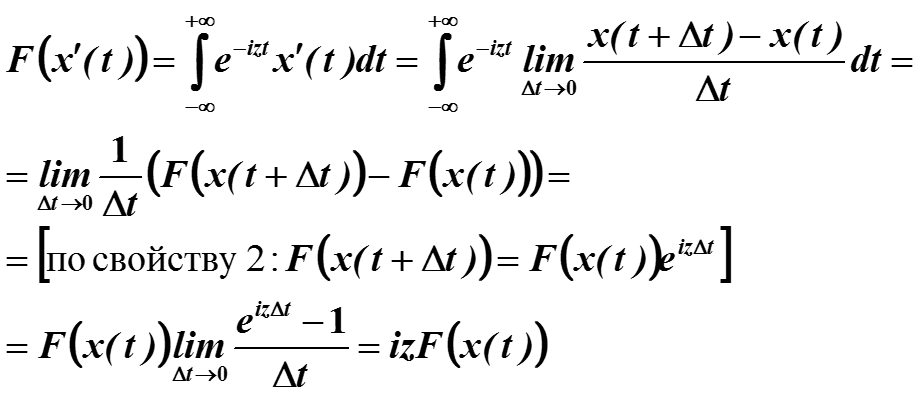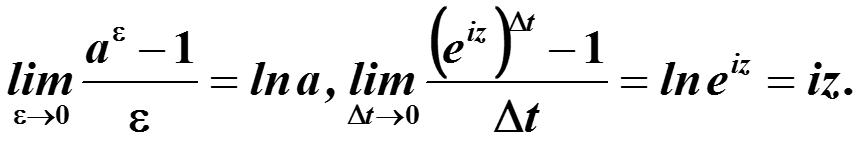-
Если Gcos(z) – косинус-преобразование функции g(t), а Hsin(z) – синус-преобразование функции h(t), то преобразование Фурье произвольной функции x(t) можно представить как сумму косинус- и синус-преобразований:
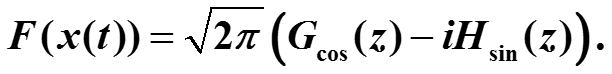
3.7. Синус- и косинус-преобразования
-
Пример. Найти преобразование Фурье функции
-
Функция четная, поэтому ее Фурье-образ можно вычислить через косинус-преобразование.
-
Дважды интегрируем по частям и получаем

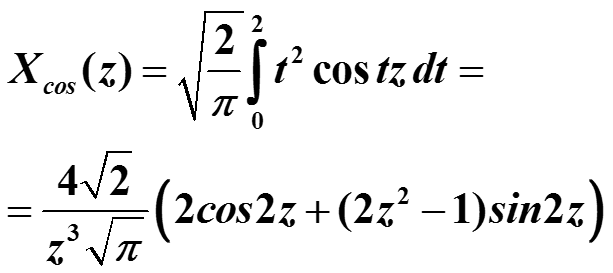
3.7. Синус- и косинус-преобразования
-
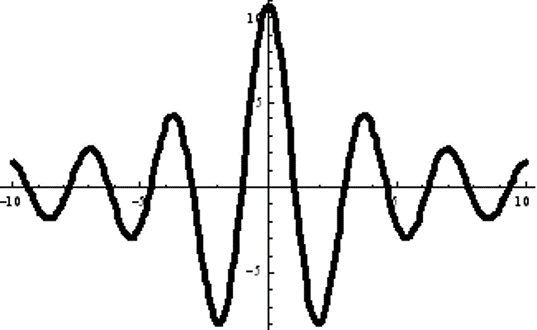
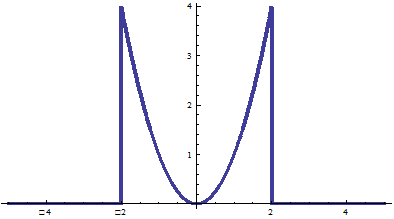
График сигнала и его косинус-преобразование
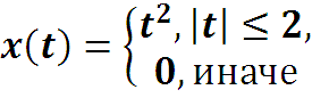
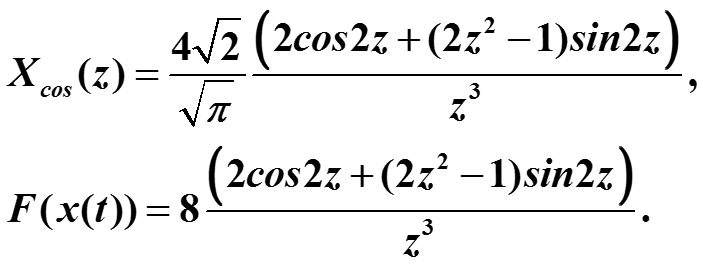
3.8. Примеры Фурье-преобразований
-
Пример. Найти преобразование Фурье функции
-
где a > 0.
-
Функция четная, ее преобразование Фурье сводится к косинус-преобразованию.
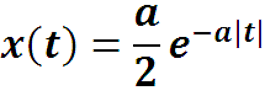
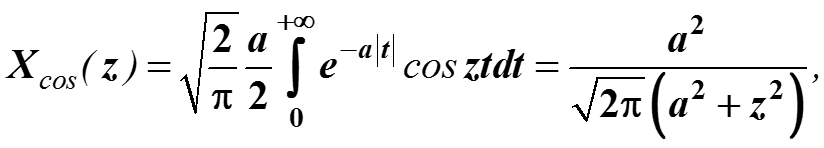
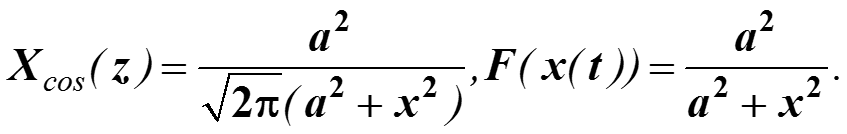
3.8. Примеры Фурье-преобразований
-
Графики функций (при а = 1)
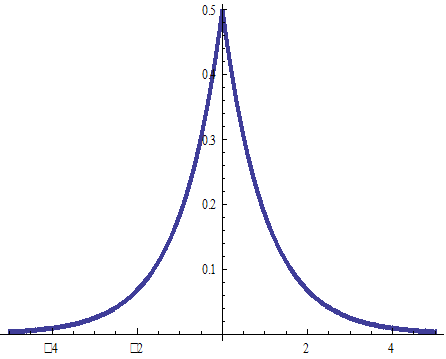
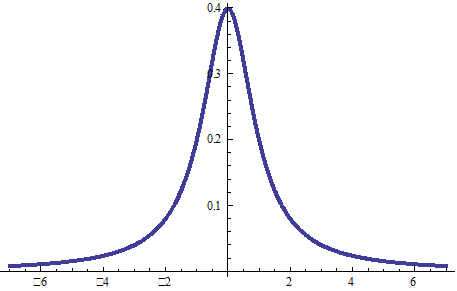
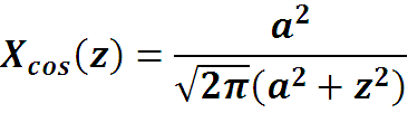
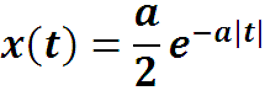
3.8. Примеры Фурье-преобразований
Преобразование получено таким образом:
Вначале найдем неопределенный интеграл
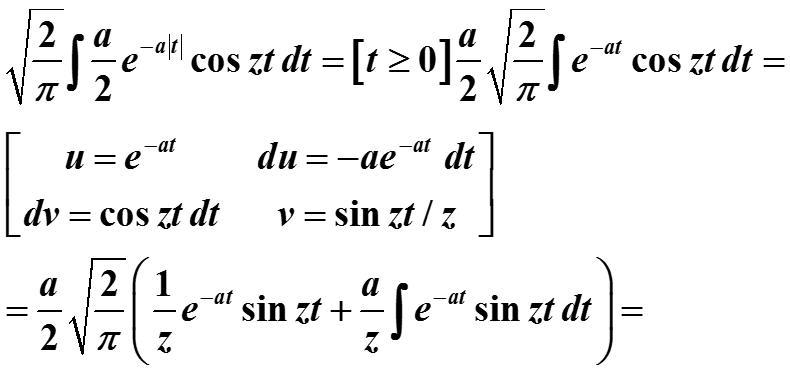
3.8. Примеры Фурье-преобразований
Далее получаем уравнение относительно искомого неопределенного интеграла:
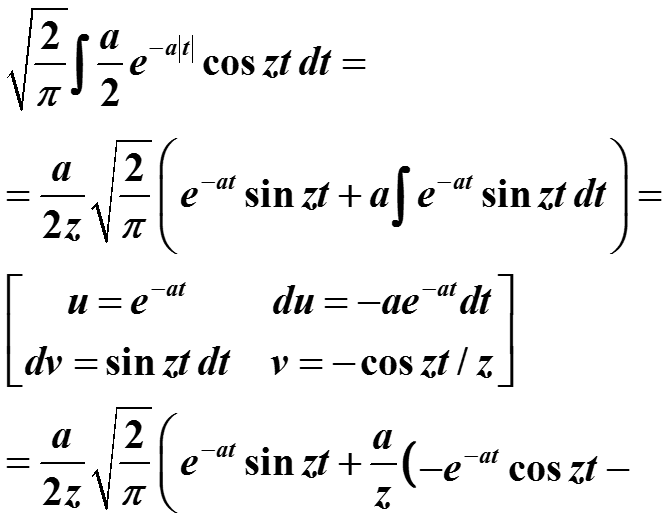
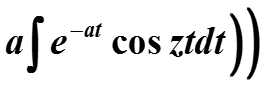
3.8. Примеры Фурье-преобразований
Положим, что искомый интеграл равен Х :
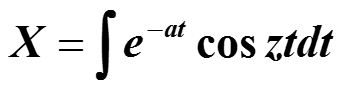
И решим полученное уравнение относительно этого неизвестного Х :
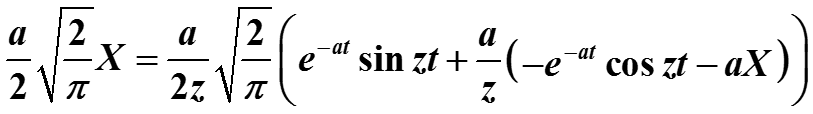
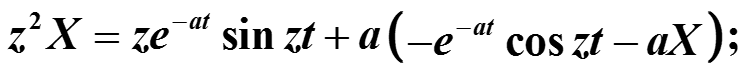
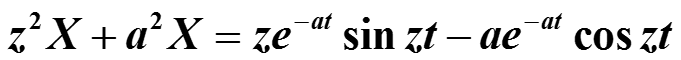
3.8. Примеры Фурье-преобразований
После алгебраических преобразований получаем значение Х :
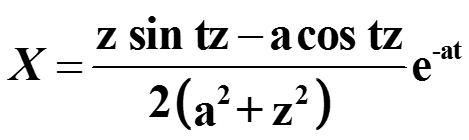
Найдем определенный интеграл
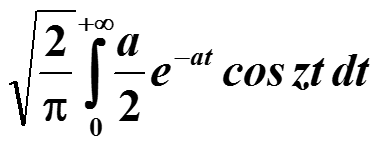
учитывая что a > 0
3.8. Примеры Фурье-преобразований
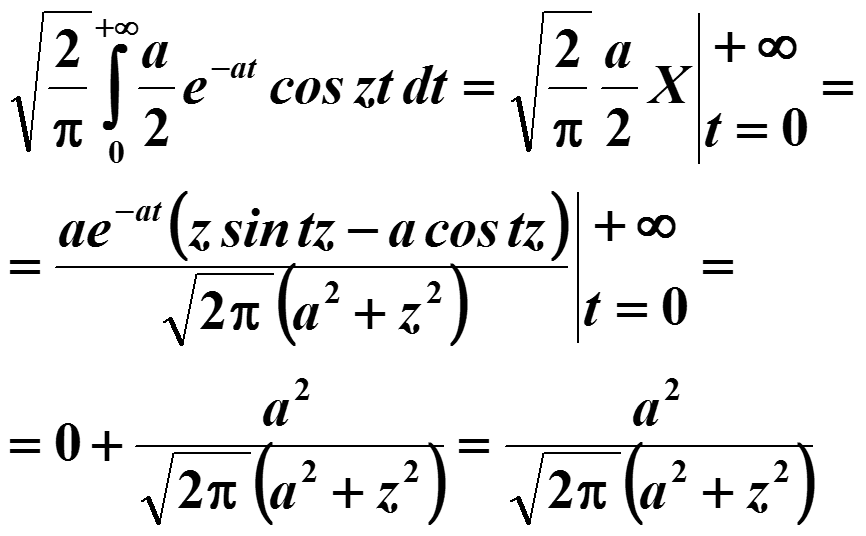
3.8. Примеры Фурье-преобразований
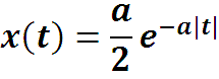
Интеграл от сигнала
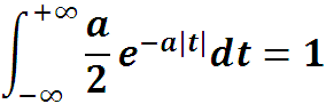
по всей вещественной оси равен
-
- для этого подобран множитель a/2 . Это свойство понадобится при изучении δ-функции.
-
Заметим, что при функция стремится к нулю во всех точках, кроме t=0, а в этой точке функция стремится к бесконечности. То есть, функция x(t) стремится к δ-функции, а ее Фурье – образ стремится к постоянной функции, равной 1.
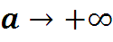
3.8. Примеры Фурье-преобразований
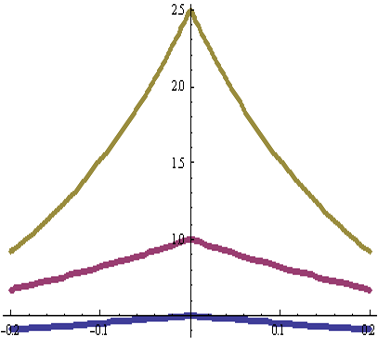
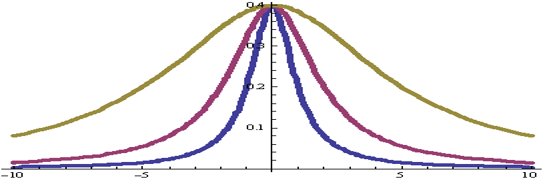
Функция x(t) стремится к δ-функции, а ее Фурье- образ к постоянной величине, равной 1.
3.8. Примеры Фурье-преобразований
Найдем Фурье-образ прямоугольной функции

-
Функция четная, поэтому достаточно вычислить ее косинус-преобразование.

3.8. Примеры Фурье-преобразований
-
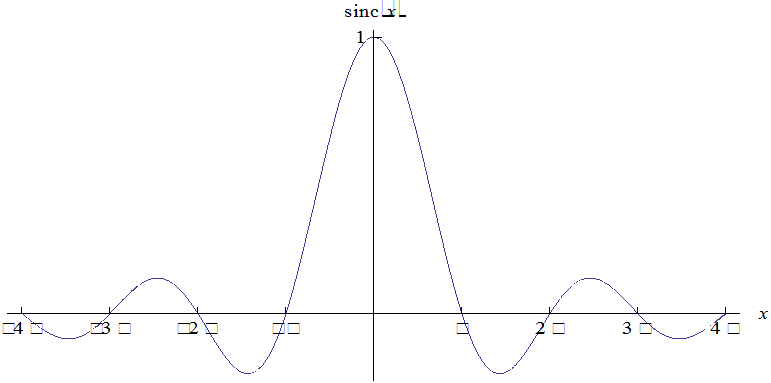
В радиоэлектронике часто используется специальная функция sinc(.) – функция Ланцоша. Определение этой функции
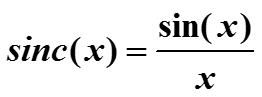
-
В точке 0 функция sinc(.) определяется по непрерывности, т.е. равна 1.
3.8. Примеры Фурье-преобразований
-
Фурье-образ прямоугольной функции можно выразить через функцию sinc t.
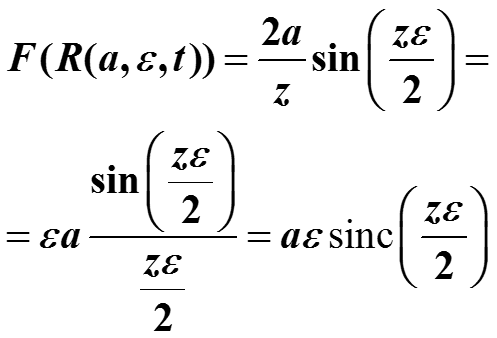
3.8. Примеры Фурье-преобразований
-
Для прямоугольного импульса a=1/ε . Его Фурье-образ равен
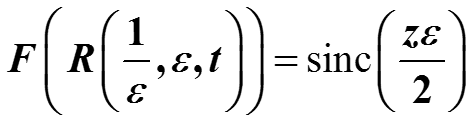
-
Если ε -> 0, то эта функция стремится к 1 для любого z.
-
То есть снова получено (математически более строго), что преобразование Фурье от δ-функции (здесь она моделируется прямоугольным импульсом) равно
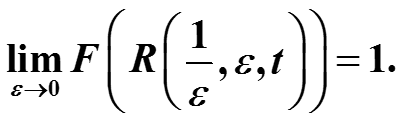
3.9. Свойства преобразования Фурье
-
Свойства преобразования Фурье :
-
1. Линейность F(a·f(t) + b·g(t)) = a·F(f(t)) + b·F(g(t)).
-
2. Свойство сдвига по времени: для постоянной τ
-
3. Свойство сдвига по частоте: для постоянной z0
-
4. Масштабирование (a не равно 0 )
-
5. Преобразование производной
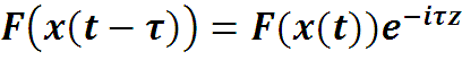

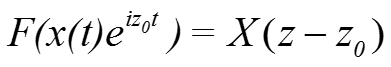
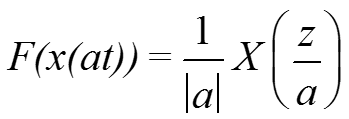
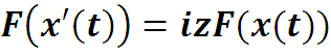
3.9. Свойства преобразования Фурье
-
Доказательство свойств:
-
1. Очевидно по свойству линейности интеграла: интеграл суммы равен сумме интегралов.
-
2. Доказывается заменой переменной
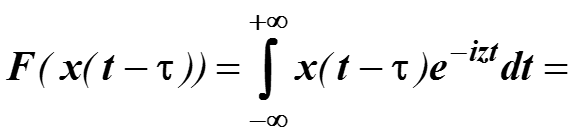

-
Выполняем замену: u = t – τ, тогда du = dt , а пределы интегрирования не меняются.
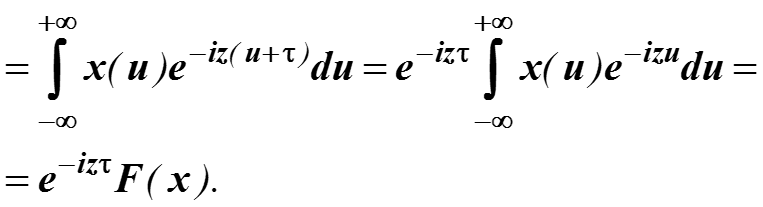
3.9. Свойства преобразования Фурье
-
3. Доказываем элементарным преобразованием степени
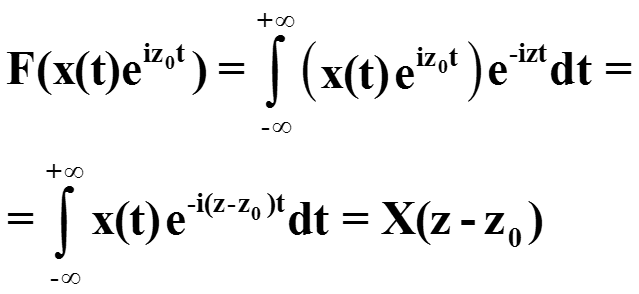

-
Отсюда следует свойство сдвига в частотной области :
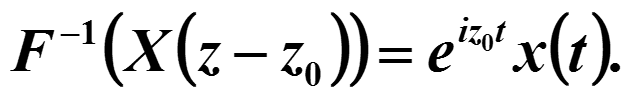
3.9. Свойства преобразования Фурье
-
4. Докажем заменой переменных. При а > 0 замена u = at
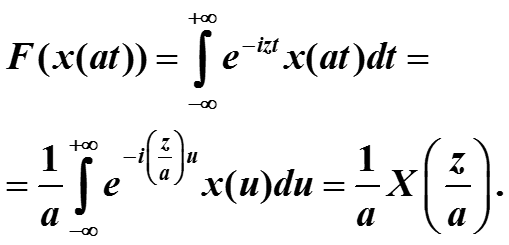
-
При а < 0 та же замена u = at, при этом пределы интегрирования меняются на противоположные. Обратная замена пределов дает знак «минус». Так получается свойство для общего случая.
-
5. Докажем применением замечательного предела
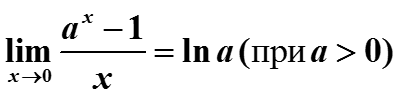
3.9. Свойства преобразования Фурье
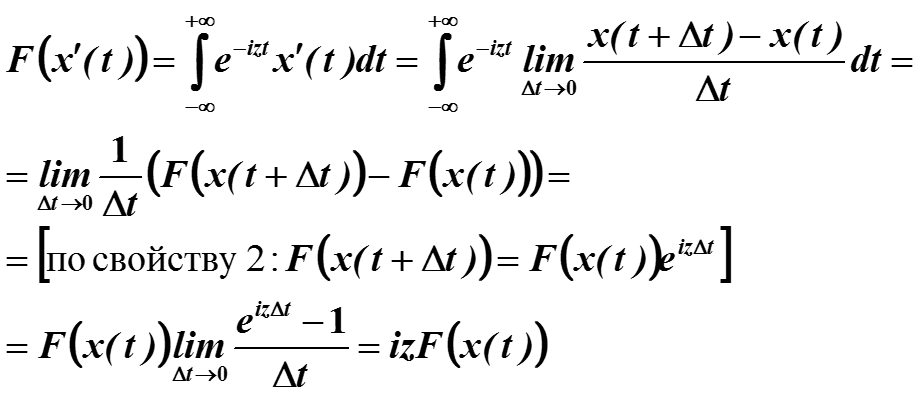
-
по замечательному показательному пределу при а > 0
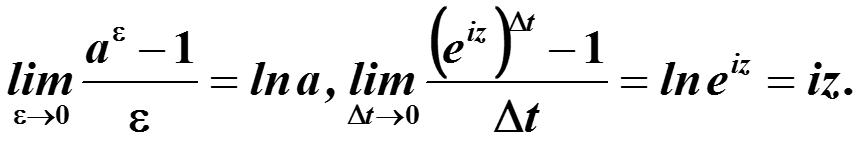
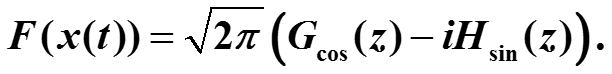

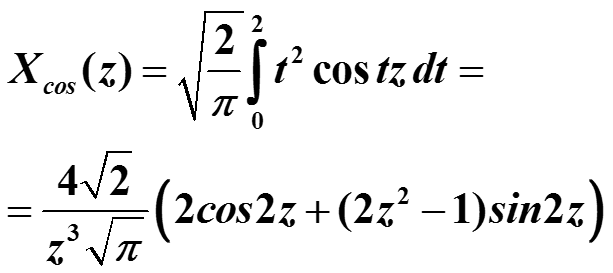

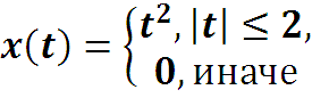

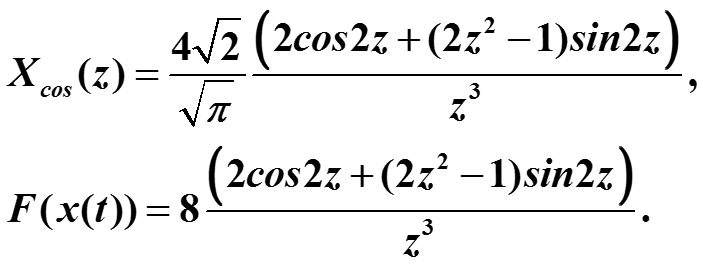
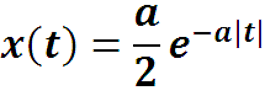
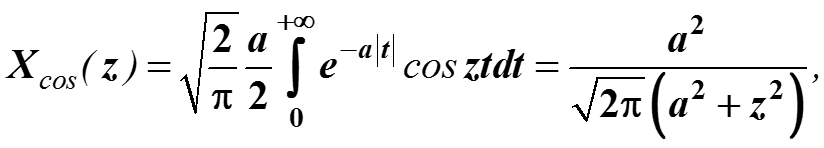
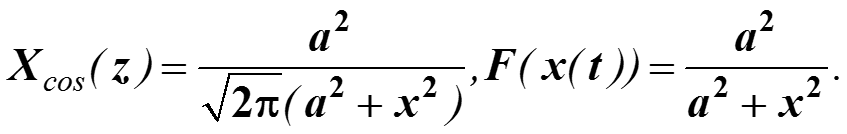


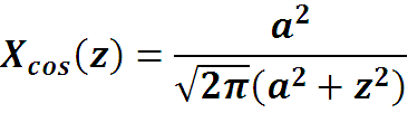
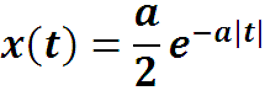
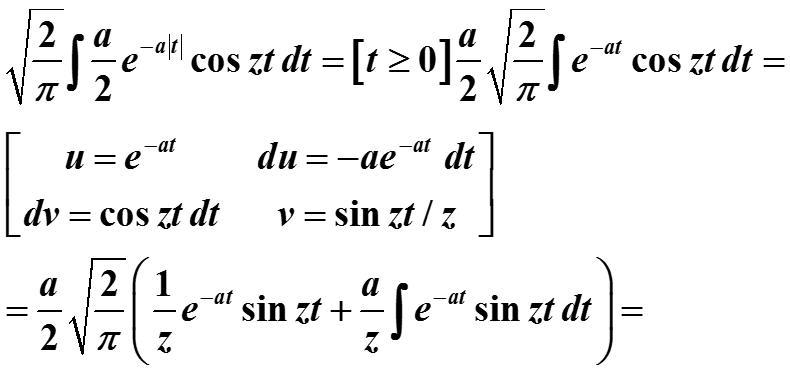
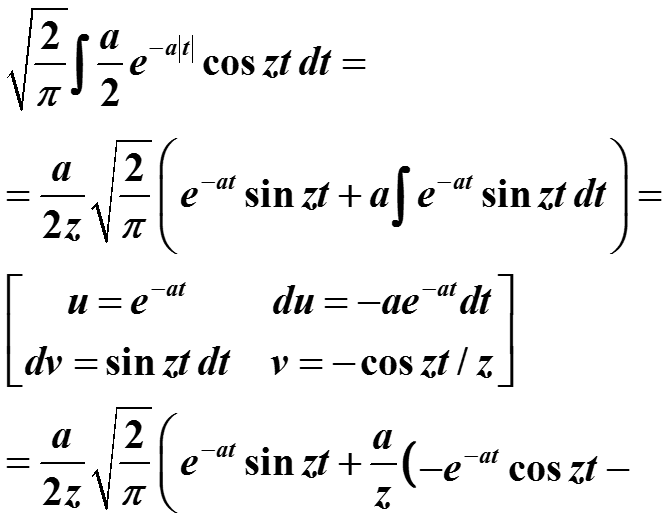
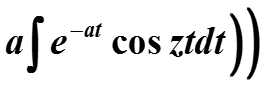
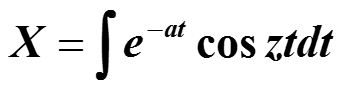
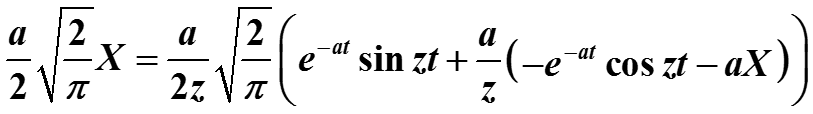
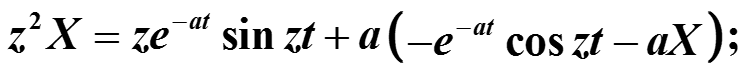
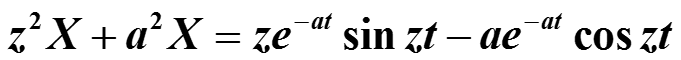
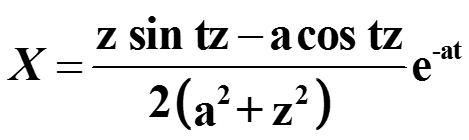
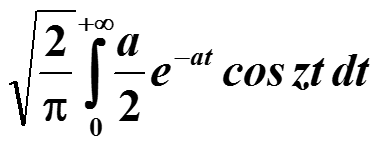
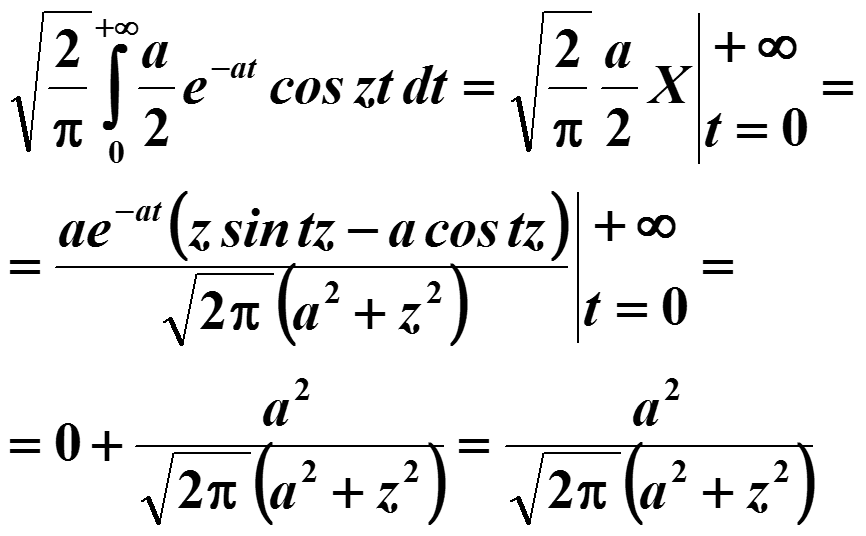
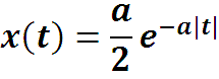
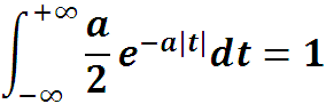
![]()




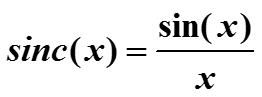

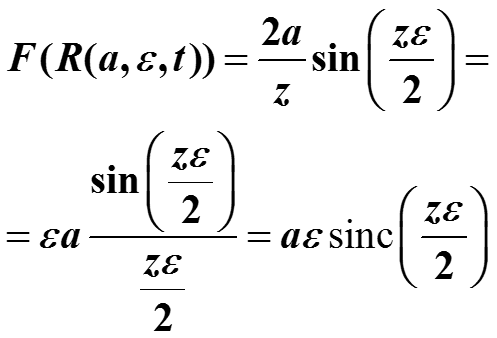
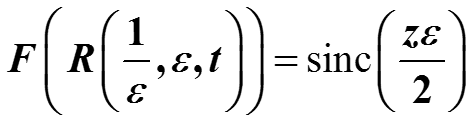
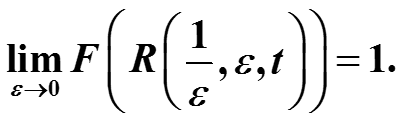
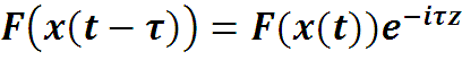
![]()
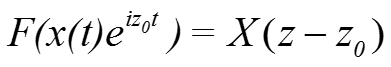
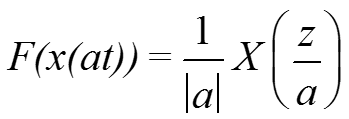
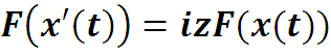
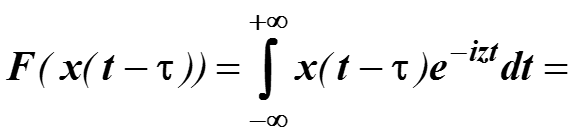
![]()
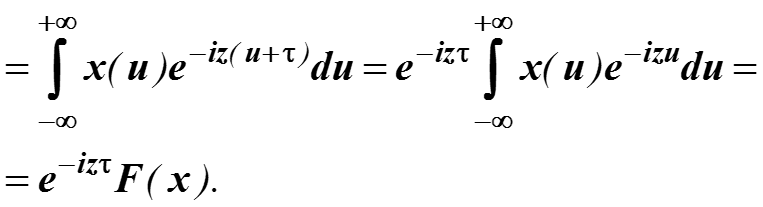
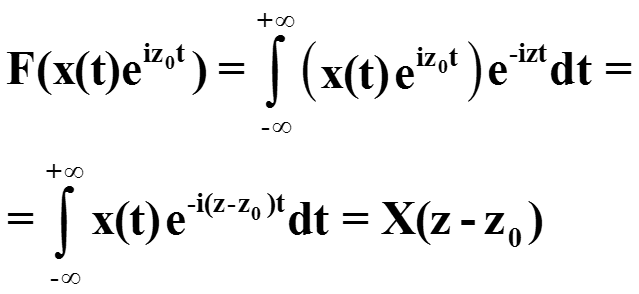
![]()