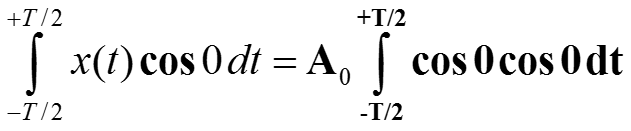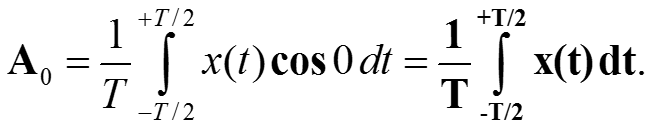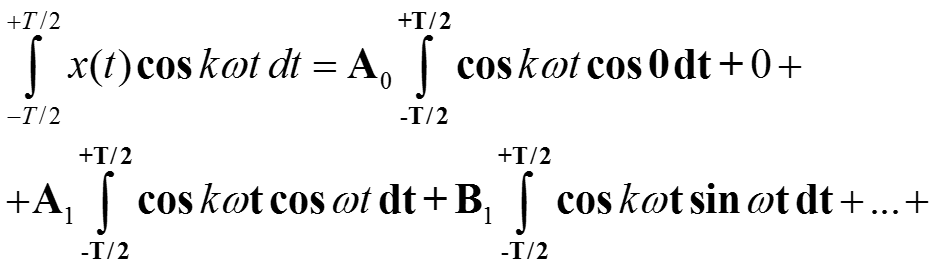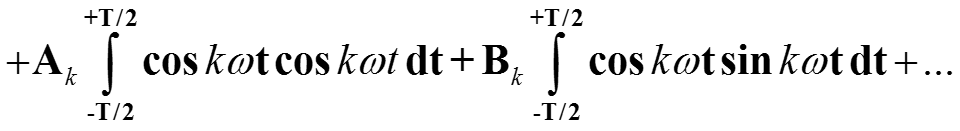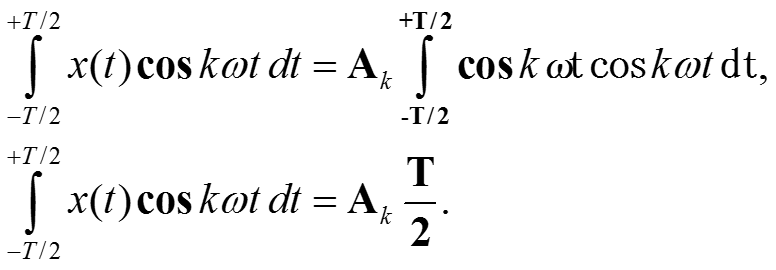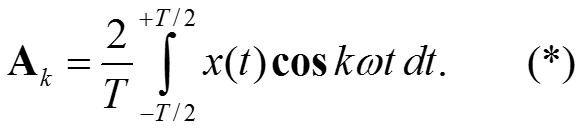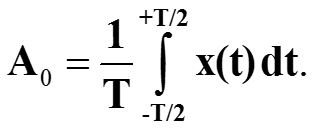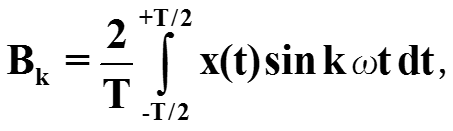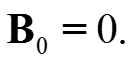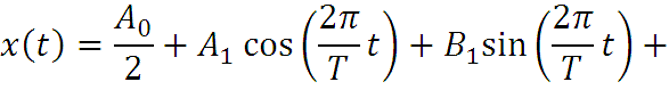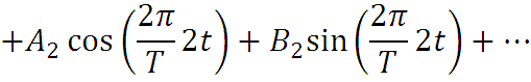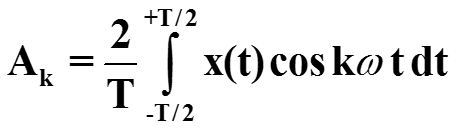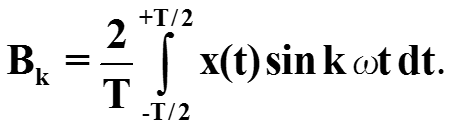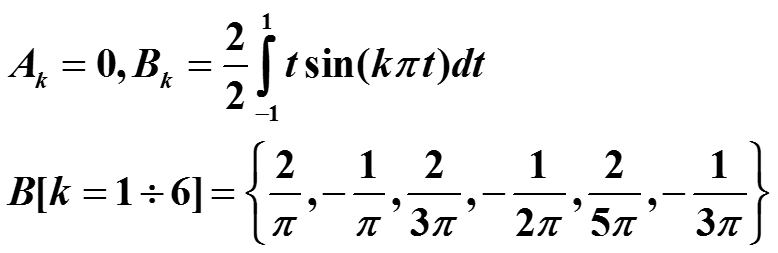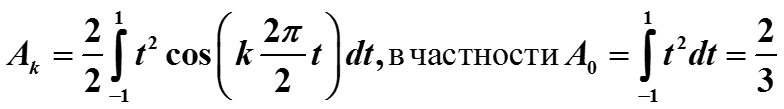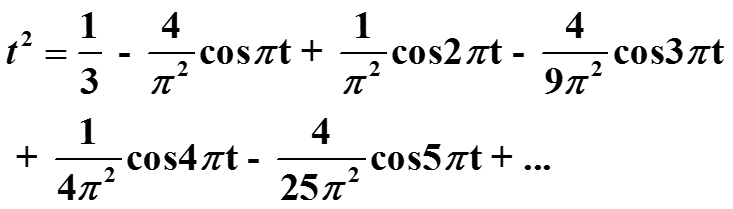-
Так как по результатам п 3.1. сигналы cos nωt и cos mωt при n≠m для всех целых n и m ортогональны и сигналы sin nωt и cos mωt для всех целых n и m также ортогональны, то все интегралы, кроме выражения левой части и первого слагаемого правой части обращаются в нуль. Тогда получаем
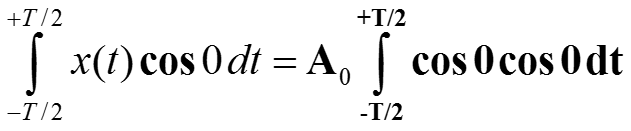
-
По результатам п 3.1.квадрат нормы cos 0 равен T, Тогда получаем
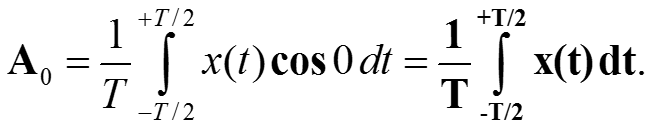
Page 18
3.2. Коэффициенты разложения в ряд Фурье
-
Коэффициенты Ak, Bk вычисляем аналогично, для построения Ak умножаем обе части (*) на cos kωt и проинтегрируем обе части выражения
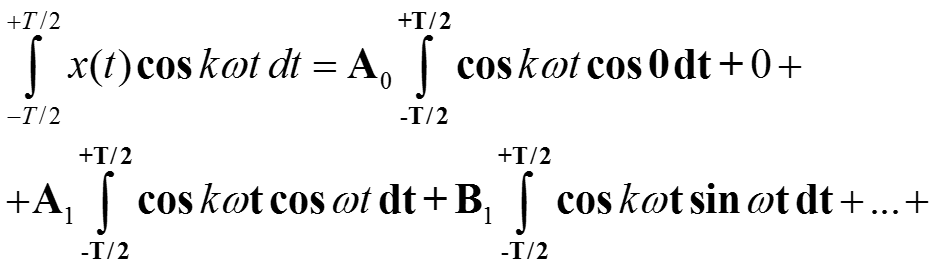
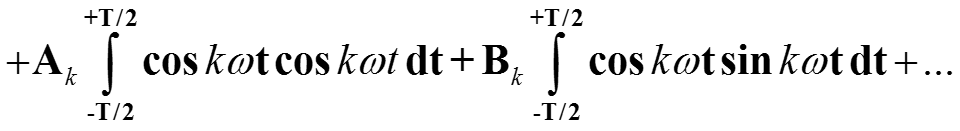
Page 19
3.2. Коэффициенты разложения в ряд Фурье
-
Ввиду ортогональности все интегралы обращаются в нуль, кроме интеграла с коэффициентом Ak, и с учетом нормы cos kωt получаем выражение
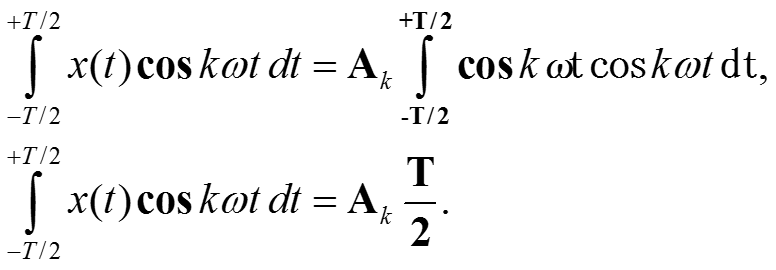
Page 20
3.2. Коэффициенты разложения в ряд Фурье
-
Отсюда коэффициент Ak для k=1,2,… равен
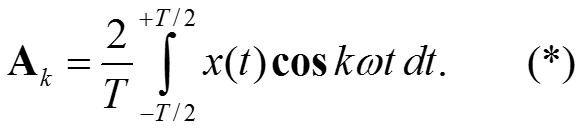
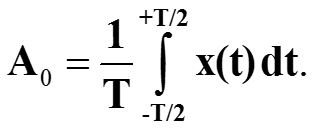
-
коэффициент Bk вычисляем аналогично, для этого умножаем обе части (*) на sin kωt и интегрируем обе части полученного выражения, окончательно
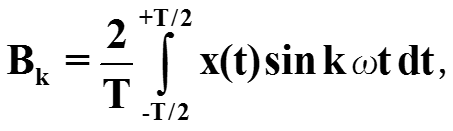
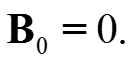
Page 21
3.2. Коэффициенты разложения в ряд Фурье
-
Если разложение в ряд Фурье функции x(t) записать в виде
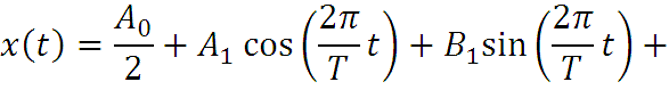
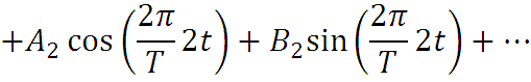
-
То формула для Ak справедлива и для k=0. Таким образом, для k=0,1,2,…
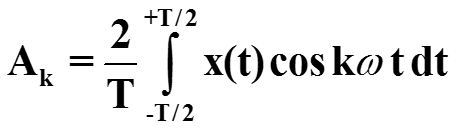
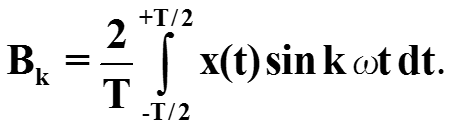
Page 22
3.2. Коэффициенты разложения в ряд Фурье
-
Легко показать, что при разложении нечетной функции коэффициенты ряда Фурье при базисных функциях cos(·) равны нулю, то есть разложение разложения нечетной функции не содержит базисных функций cos(·).
-
При разложения четной функции ряд Фурье не содержит базисных функций sin(·).
-
Ряд Фурье хорошо приближает периодические функции. Можно рассматривать любую (в том числе непериодическую) функцию на отрезке и разлагать ее в ряд Фурье только на отрезке, для непериодической функции удобно считать длину этого отрезка ее периодом.
3.2. Коэффициенты разложения в ряд Фурье
-
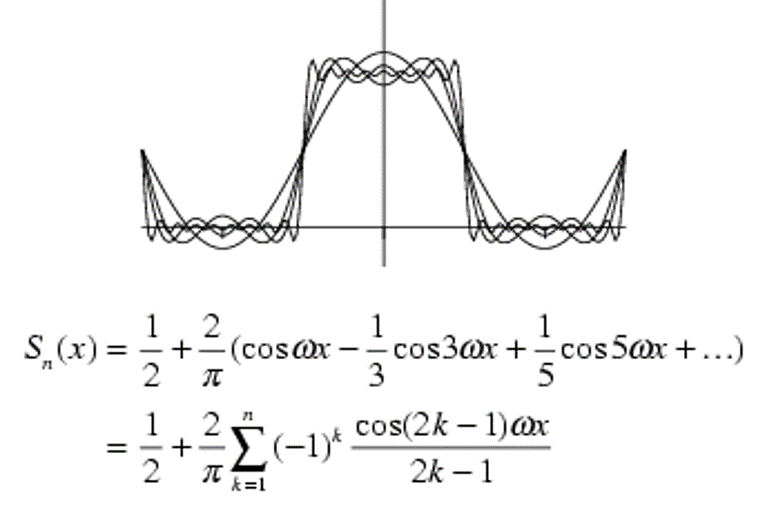
Прямоугольная функция четная. Ряд Фурье для прямоугольной функции содержит только cos(•): Коэффициенты Bk будут равны нулю.
Page 24
3.2. Коэффициенты разложения в ряд Фурье
-
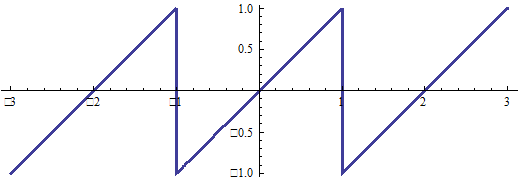
Ряд Фурье для нечетной функции:
-
Эта функция разлагается в ряд синусов, T=2, ω=π (здесь разложение до k = 4).
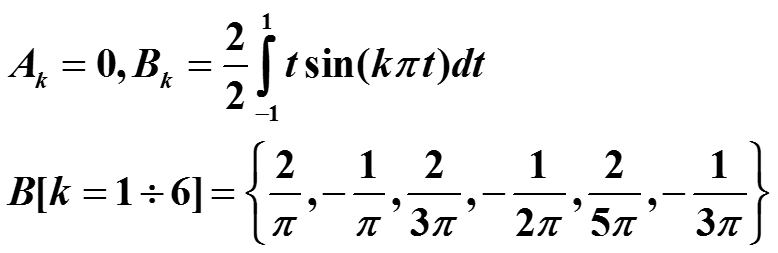
Page 25
3.2. Коэффициенты разложения в ряд Фурье
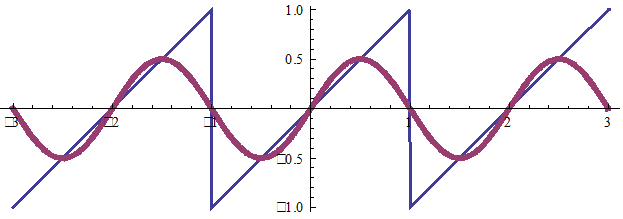
k = 1
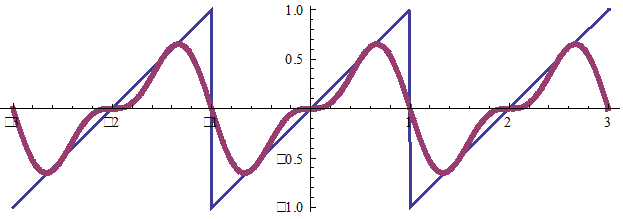
k = 2
Page 26
3.2. Коэффициенты разложения в ряд Фурье
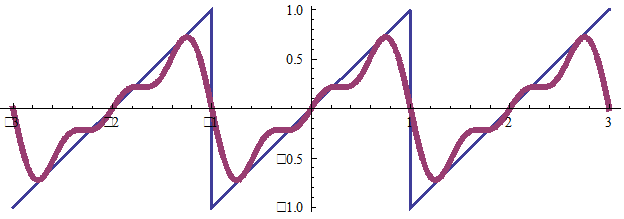
k = 3
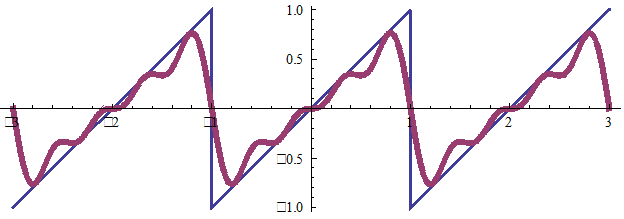
k = 4
Page 27
3.2. Коэффициенты разложения в ряд Фурье
-
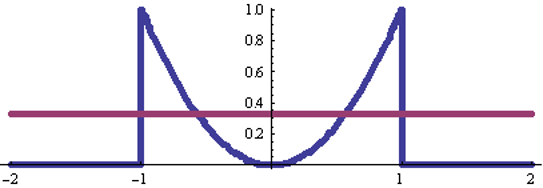
Разложим x(t) = t2 на отрезке [-1, 1], принимаем T=2. Функция четная, поэтому ряд содержит только cos(·).
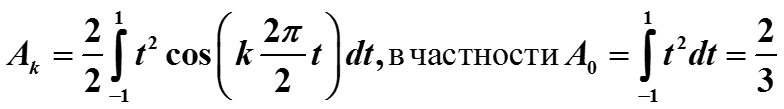
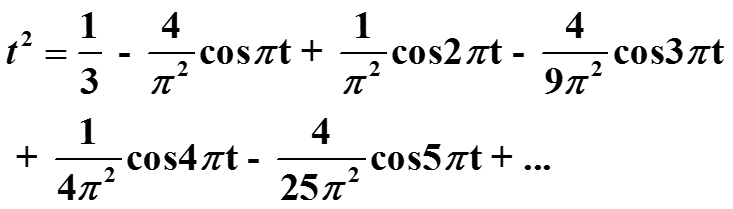
Page 28
3.2. Коэффициенты разложения в ряд Фурье
-
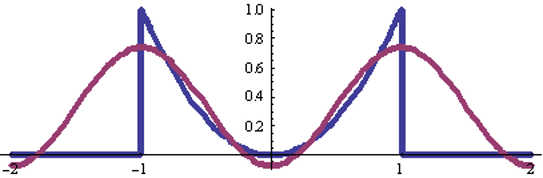
Ряд Фурье для четной функции x(t) = t2
-
на отрезке [-1,+1] (то есть, Т=2) :
k = 0
k = 1
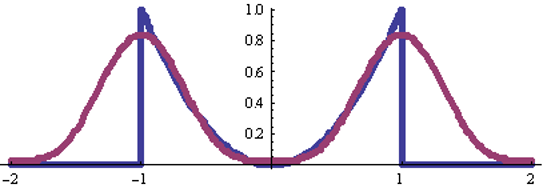
k = 2
Page 29
3.2. Коэффициенты разложения в ряд Фурье
-
Ряд Фурье для четной функции x(t) = t2 :
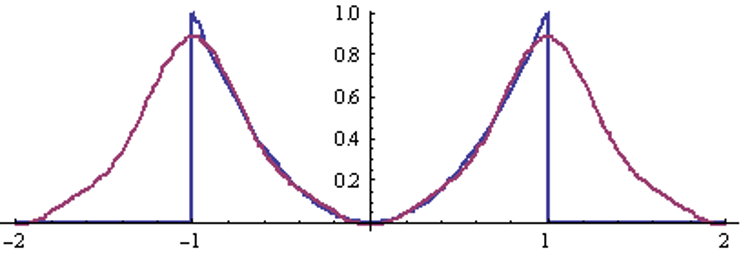
k = 3
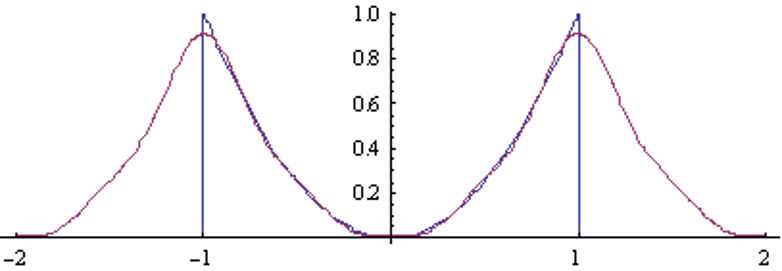
k = 4
Page 30
3.2. Коэффициенты разложения в ряд Фурье
-
Следует заметить, что для некоторых функций ряд Фурье расходится, для некоторых ряд Фурье не сходится к разлагаемой функции, в обоих случаях говорят, что функция не разлагается в ряд Фурье.

3.3.Временная и частотные области сигнала
-
Сигнал моделируется в виде функции x(t), зависящей от времени t. Говорят, что сигнал моделируется во временной области. При разложении в ряд Фурье с периодом T сигнал представляется в виде ряда от sin(·) и cos(·) от аргументов ω, 2ω, 3ω, . . ., где частота
-
ω = 2π/T.
-
Таким образом, сигнал разлагается по функциям с аргументами, содержащими частоты kω. Коэффициенты Ак и Вк называются частотными коэффициентами. Такое представление сигнала называется представлением в частотной области.
-
Из представления x(t) во временной области разложением в ряд Фурье можно получить представление в частотной области и наоборот (если существует разложение функции x(t) в ряд Фурье).
3.3.Временная и частотные области сигнала
-
Генерация электрических сигналов cos(t) и sin(t) в магнитном поле. В зависимости от скорости вращения рамки изменяется период и соответственно частота сигнала.