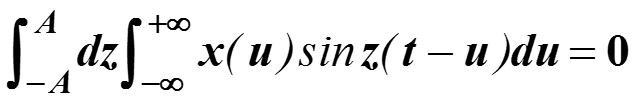
Page 46
3.6. Преобразование Фурье
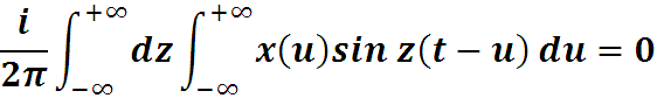
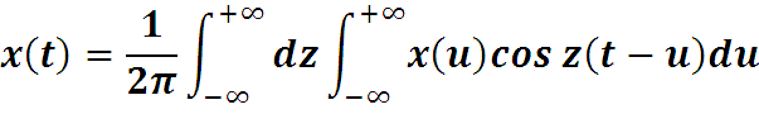
Теперь после внесения под общий знак интеграла и применения формулы Эйлера :
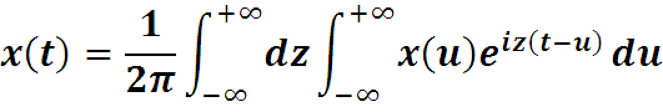
Page 47
3.6. Преобразование Фурье
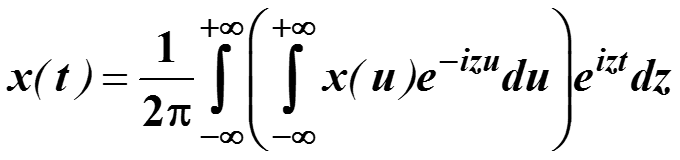
Интегральное преобразование
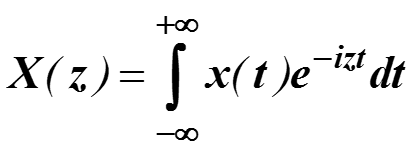
Называется прямым преобразованием Фурье. Оно записывается как
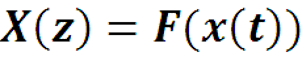
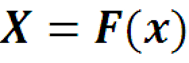
Page 48
3.6. Преобразование Фурье
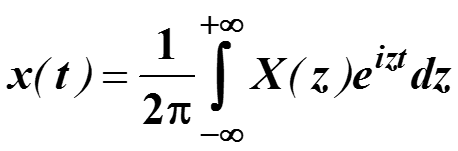
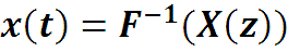
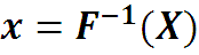
Функция X(z) называется Фурье-образом функции x(t), а функция x(t) называется Фурье-прообразом функции X(z). По аналогии со спектром амплитуд ряда Фурье, |X(z)| называется амплитудно-частотной сигнала x(t), а Arg(X(z)) фазовой характеристикой сигнала x(t).
Page 49
3.6. Преобразование Фурье
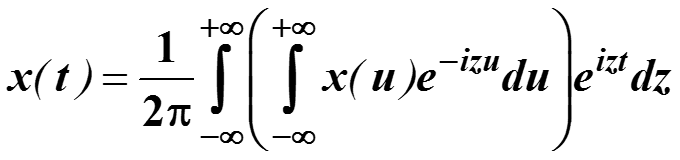
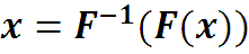
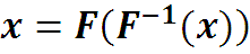
Page 50
3.6. Преобразование Фурье
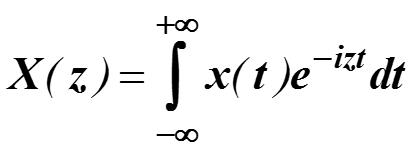
То есть вещественная функция вещественного аргумента t (времени) преобразуется в комплексную функцию от вещественного аргумента z (частоты). В общем случае можно рассматривать и t и z как комплекс-ные переменные. Тогда преобразования Фурье – это преобразования комплексной плоскости на комплексную плоскость.
Page 51
3.7. Синус- и косинус-преобразования
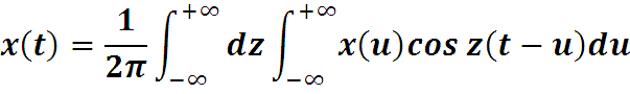
Представим cos z(t-u) как косинус разности и получим (*)
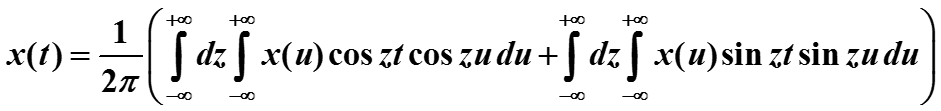
Если функция x(u) четная, то во втором интеграле функ- ция x(u) sin(zu) нечетная по u интеграл по du на симмет-ричном отрезке от нее будет равен нулю. Поэтому для четной функции x(u) второе слагаемое обращается в нуль.
Page 52
3.7. Синус- и косинус-преобразования
Для четной функций x(t)
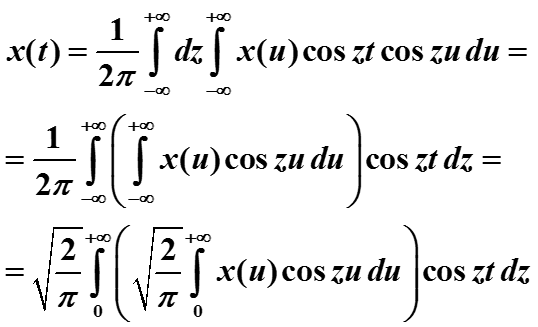
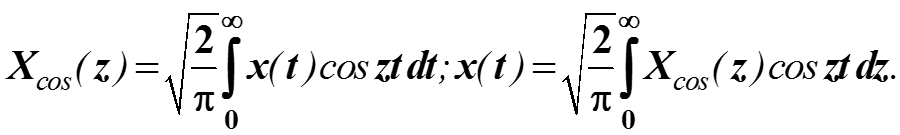
Они называются соответственно прямым и обратным косинус-преобразованием. Косинус-преобразование переводит вещественную функцию в вещественную.
Page 53
3.7. Синус- и косинус-преобразования
Преобразование Фурье от четной функций x(t) равно:
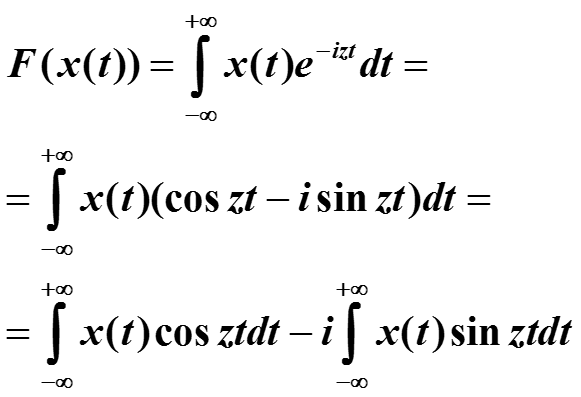
3.7. Синус- и косинус-преобразования
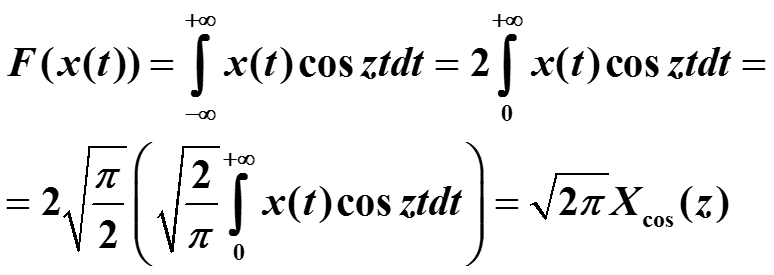
Получен результат : если x(t) - четная функция, то
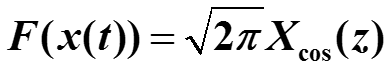
3.7. Синус- и косинус-преобразования
3.7. Синус- и косинус-преобразования
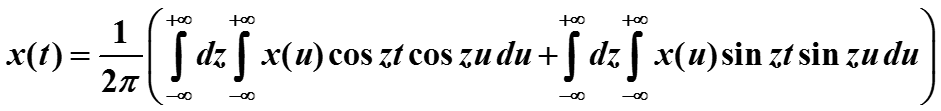
Функция x(u) cos(zu) четная и интеграл от нее обращается в нуль, потому что пределы интегрирования –А , +А. Тогда из равенства
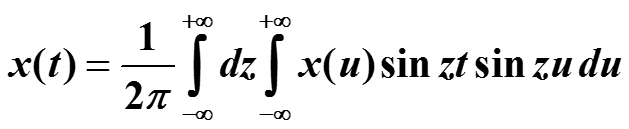
получаем прямое и обратное синус-преобразование
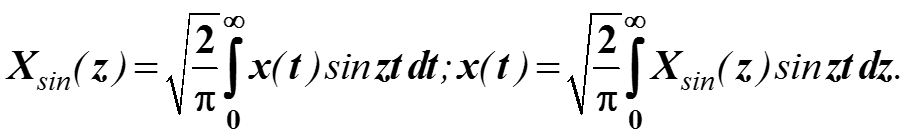
3.7. Синус- и косинус-преобразования
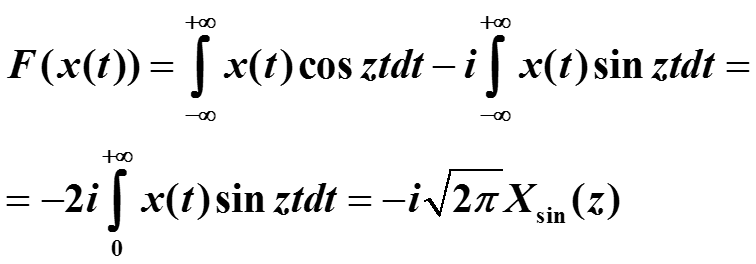
3.7. Синус- и косинус-преобразования
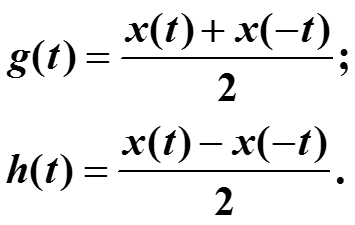
![]()
тогда g(t) – четная функция, h(t) – нечетная функция и
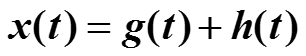
3.7. Синус- и косинус-преобразования
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.