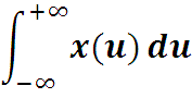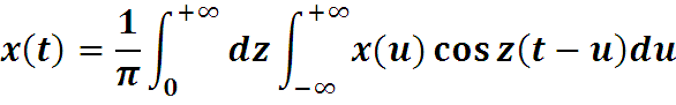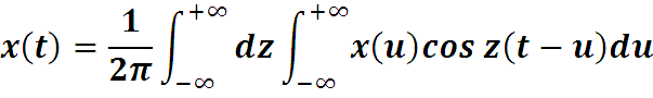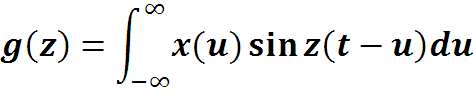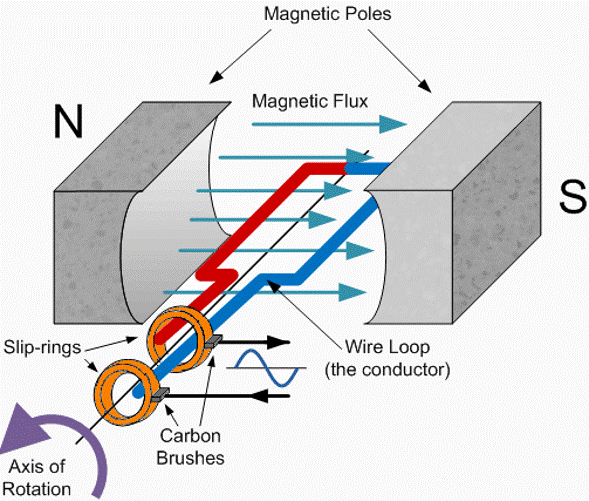
3.3.Временная и частотные области сигнала
-
Зависимость напряжения сигнал от угла рамки в линиях напряженности магнитного поля.
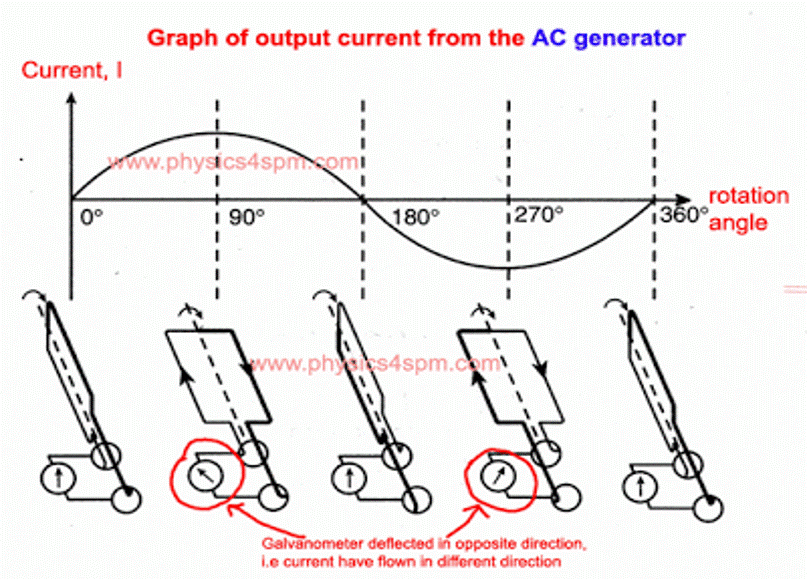
3.3.Временная и частотные области сигнала
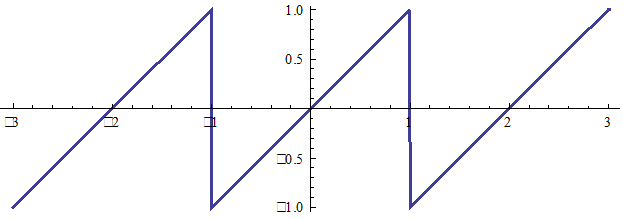
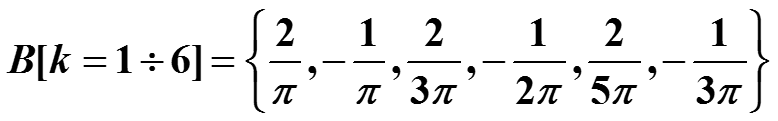
2/π
Page 35
3.3.Временная и частотные области сигнала
-
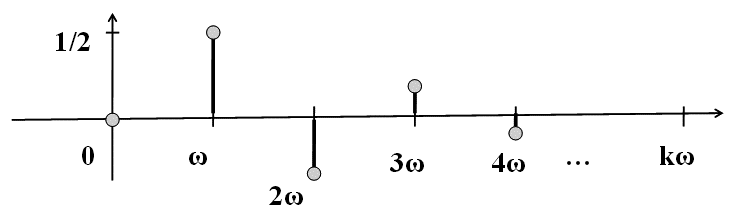
Если увеличить период T, то частота ω уменьшится и на график коэффициентов (частотный график) изменится. точки (или отрезки в зависимости от того, как представлены коэффициенты на графике):
-
Для разложения «пилы» предыдущего слайда с удвоенным параметром ω график частот станет такой:
1/2
4ω
ω
2ω
3ω
0
kω
Page 36
3.3.Временная и частотные области сигнала
-
Можно и дальше увеличивать период T, при график частот приближается к некоторой кривой.
-
Ряд приближается к интегральному преобразованию, это преобразование сигнал в некоторую функцию (частотную функцию):
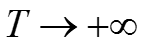
1/2
4ω
ω
2ω
3ω
0
kω
Это преобразование Фурье исходного сигнала x(t). Штриховая линия – Фурье-образ сигнала x(t).
Page 37
3.4. Комплексная форма ряда Фурье
-
Известна формула Эйлера, связывающая экспоненту с тригонометрическими функциями.
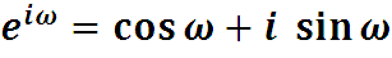
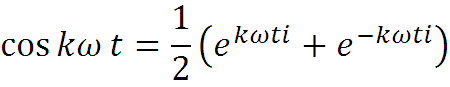
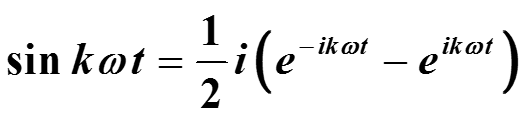
Заменяя sin() и cos() экспонентами, получаем ряд Фурье в следующем виде:
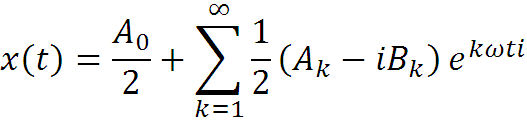
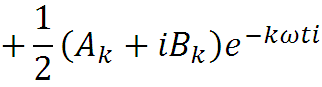
Page 38
3.4. Комплексная форма ряда Фурье
-
Введем новые обозначения
-
где Ck и C-k комплексные числа. Запишем ряд Фурье в комплексной форме:
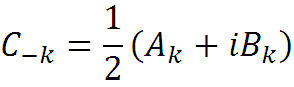
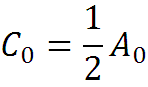
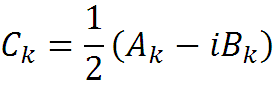
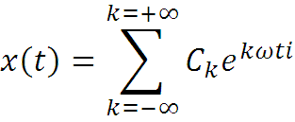
Ck и C-k комплексно сопряженные числа. Зная один из коэффициентов Ck или C-k, можно найти другой, поменяв знак мнимой части. Это означает, что в комплексной форме достаточно разложить сигнал x(t) только для k = 0, 1, 2, … или для k = 0, -1, -2, … и изменив знак мнимой части, получить остальные коэффициенты разложения.
Page 39
3.4. Комплексная форма ряда Фурье
-
Множество вещественных чисел
-
называется спектром амплитуд сигнала.
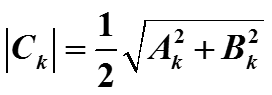
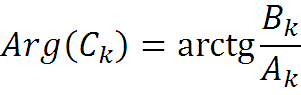
- спектр фаз
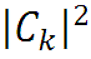
- спектр мощности (или энергии) сигнала (подробнее рассмотрим при изучении равенства Парсеваля).
Page 40
3.5. Интеграл Фурье
-
Разложение в ряд Фурье предполагает знание периода T = 2π/ω разложения. Ряд Фурье содержит амплитуды частот, из которых складывается сигнал.
-
Преобразование Фурье, к рассмотрению которого мы переходим, не зависит от периода T и вместо последовательности амплитуд частот строит функцию амплитуд (плотность спектра).
-
Для построения преобразования Фурье достаточно предположить, что существуют все участвующие в выводе формулы интегралы, особенно отметим существование интеграла
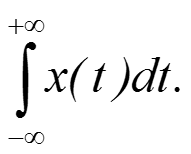
Page 41
3.5. Интеграл Фурье
-
Заменяя в ряде Фурье коэффициенты их выражениями через интегралы, переходим к пределу при периоде T стремится к бесконечности.
-
Рассматриваем ряд как функцию, получается сумма значений функции в левых точках прямоугольников, умноженных на приращение аргумента, то есть приближенное значение интеграла. Переходя к пределу по T, получаем требуемый интеграл Фурье.
-
Для построения преобразования Фурье представим ряд Фурье в виде интеграла, который называется интегралом Фурье.
-
Начинаем вывод интеграла Фурье с ряда Фурье :
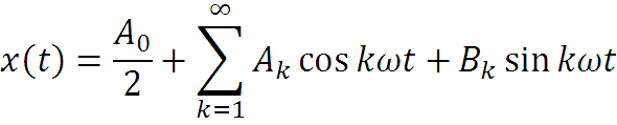
Page 42
3.5. Интеграл Фурье
-
Коэффициенты подставим в ряд
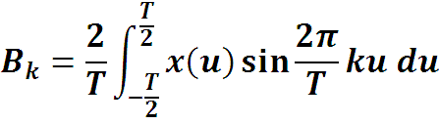
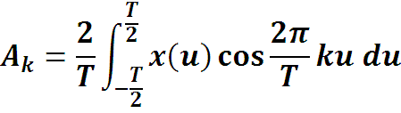
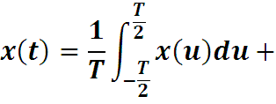
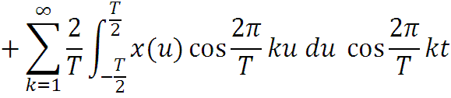
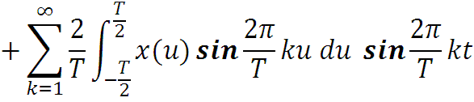
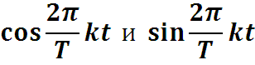
Функции не зависят от переменной интегрирования u, как постоянные величины их можно внести под знак интеграла. По формуле
преобразуем подынтегральное выражение :
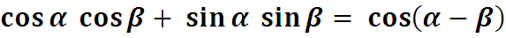
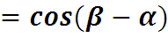
3.5. Интеграл Фурье
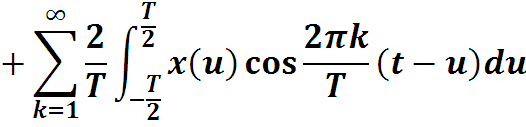
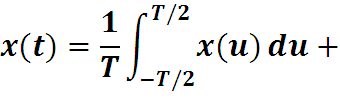
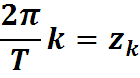
Положим
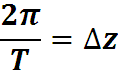
Тогда сигнал x(t) разлагается в ряд:
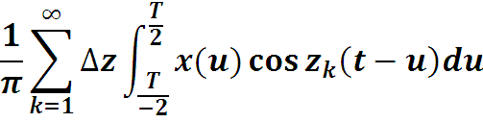
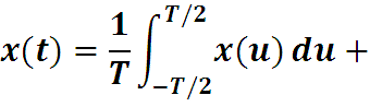
Page 44
3.5. Интеграл Фурье
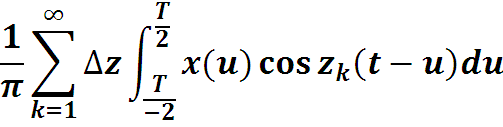
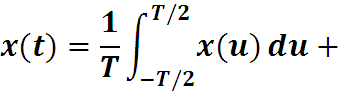
-
Eсли то сумма стремится к интегралу по z. При этом по предположению интеграл
-
существует, то есть он имеет конечное значение. Тогда первое слагаемое ряда стремится к нулю.
-
В пределе
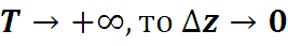
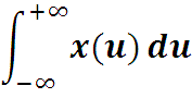
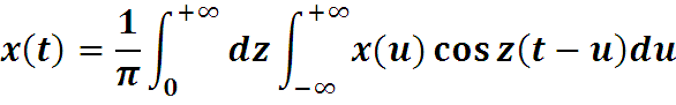
Page 45
3.5. Интеграл Фурье
-
Ввиду четности по z cos z(t-u) удвоим предел интегри-рования, результат разделим на 2 и окончательно получим интеграл Фурье:
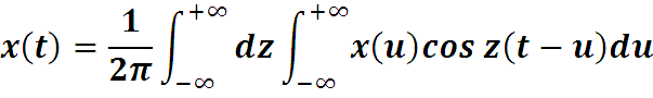
Вместе с интегралом Фурье рассмотрим функцию
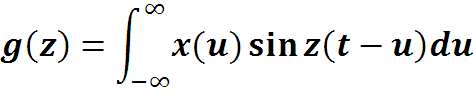
Если этот интеграл существует, то g(z) – нечетная функция по z. Если интегрировать эту функцию на интервале [A, -A] , то



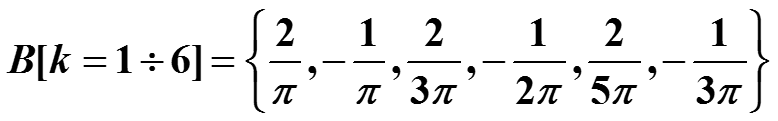

![]()
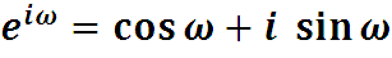
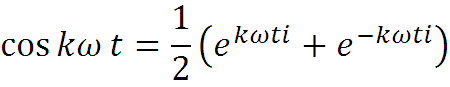
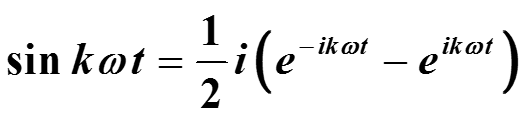
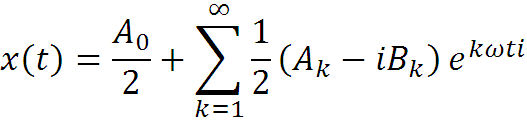
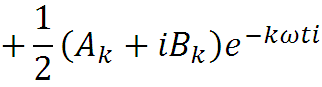
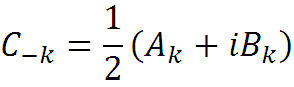
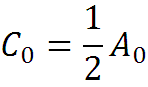
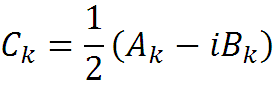
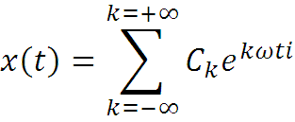
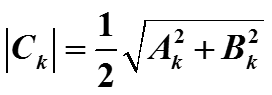
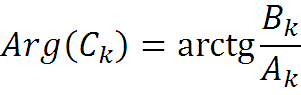
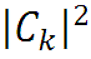
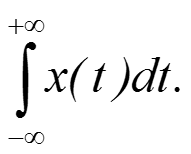
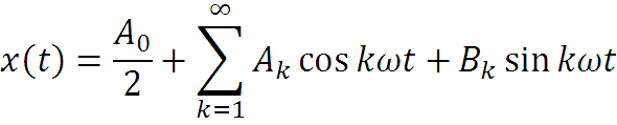
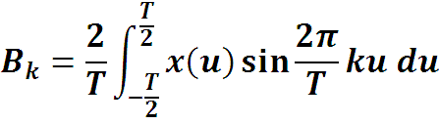
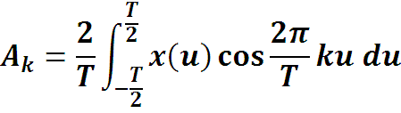
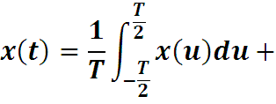
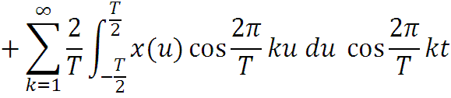
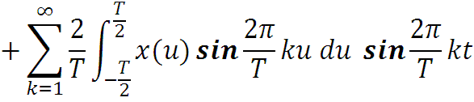
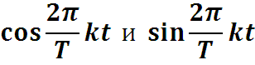
![]()
![]()
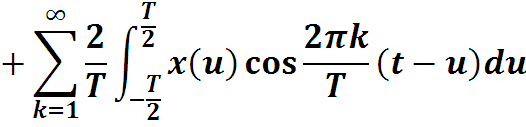
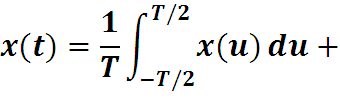
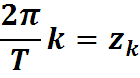
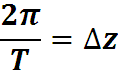
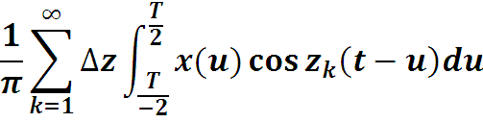
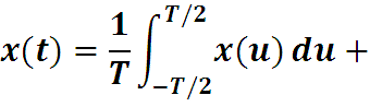
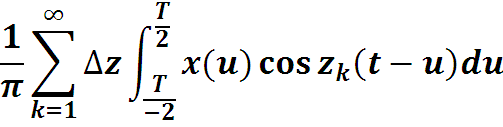
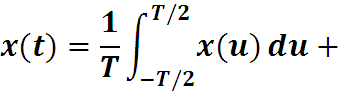
![]()