Понятие динамической системы происходит из классической механики. Это системы, описывающие поведение множества материальных точек в зависимости от времени с помощью конечного набора числовых параметров, которые удовлетворяют системе дифференциальных уравнений первого порядка. Для целей данного курса достаточно считать, что динамическая система – это система, описываемая конечным набором входных и выходных параметров, которые определены на некотором интервале времени.
Простейшая динамическая система имеет один входным и один выходным параметр и состоит из одного элемента, будем называть такую упрощенную систему объектом.
3
4.1. Уравнение свертки
Параметры представляют собой функции от времени, обозначим входной параметр как функцию x(t) , а выход-ной как y(t). Мы рассматриваем поведение объекта на некотором интервале времени, то есть параметры представляют собой функции от времени на этом интерва-ле. В первой части нашего курса все параметры объекта и все функции будем считать детерминированными. Выходной параметр y(t) некоторым образом зависит от входного параметра, то есть от функции x(t).
Мы рассматриваем поведение объекта на некотором интервале времени, то есть параметры представляют собой функции от времени на этом интервале. Зависимость выходного параметра от входного будем записывать в виде соотношения
4
4.1. Уравнение свертки
y(t) = F[x(t)],
где F – некоторое преобразование функции x(t) в функцию y(t).
Преобразование F называется оператором. Например, F может выражать зависимость в виде решения дифференциального уравнения. Одним из простейших видов зависимости функций является уравнение свертки
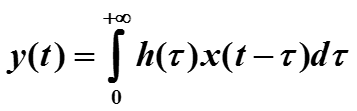
Функция h(t) называется ядром свертки. Свертка широко применяется в теории сигналов, в частности, для моделирования фильтров.
5
4.1. Уравнение свертки
В реальной ситуации ядро обычно не равно нулю только на некотором отрезке [0, M], поэтому свертка принимает вид
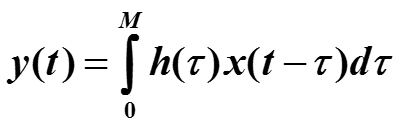
Если бы нижняя граница интервала интегрирования была бы меньше 0, например, -1, то получалось бы, что функция y(t) зависит от значения функции x(0-(-1)) в момент времени от + 1, то есть в будущем, что считаем невозможным.
6
4.1. Уравнение свертки
Следовательно, при t < 0 ядро h(t) = 0.
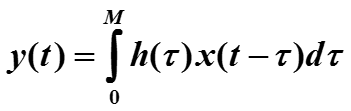
(1)
Для каждого момента времени t0 функция y(t0) зависит от функции x(t) во все моменты времени от t0 – M до t0, то есть, от «недалекого прошлого».
M называется интервалом памяти объекта.
Сокращенно соотношение (1) записывается в виде
y(t) = h(t)*x(t).
7
4.2. Идентификация объекта
Одной из основных задач в динамических системах является задача идентификации системы.
Предполагается, что исследователь может подать на вход объекта любой сигнал x(t) и наблюдать на выходе получающийся сигнал y(t).
Идентификацией системы с параметрами x(t) и y(t) называется построение оператора F, такого, что
y(t) = F[x(t)].
Процесс идентификация состоит из двух этапов:
1) выбор математической модели системы;
2) оценивание параметров выбранной модели.
В этой модели x(t) выбирает исследователь, и он наблюдает сигнал y(t) на выходе. Таким образом, требуется подобрать такой входной сигнал, чтобы найти неизвестный параметр модели - функцию h(t).
8
4.2. Идентификация объекта
Пример решения задачи идентификации.
Пусть имеется черный ящик, в который входит сигнал x(t) и выходит сигнал y(t) .
1) выбор математической модели системы;
В простейшем случае выбирается модель в виде уравнения свертки, но может выбираться и другая модель. Для идентификации черного ящика, работа которого моделируется уравнением свертки (И ТОЛЬКО ДЛЯ ЭТОЙ МОДЕЛИ ! ) задача идентификации решается при помощи свойства фильтрации -функции.
2) оценивание параметров выбранной модели.
Для уравнения свертки требуется подобрать такой входной сигнал, чтобы найти неизвестный параметр модели - функцию h(t).
9
4.2. Идентификация объекта
В качестве входного сигнала возьмем -функцию и для вычисления значения ядра h(t) на отрезке t € [0, M], используем свойство 1 -функции
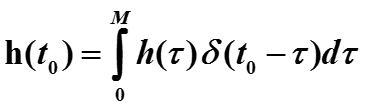
Так можно построить значение ядра в произвольной заданной точке.
Так просто решается задача идентификации для модели в виде уравнения свертки.
10
4.3. Фурье-преобразование некоторых функции
Как было показано в п.3.8., преобразование Фурье δ–функции равно постоянной
Ясно, что обратное преобразование Фурье от единицы равно δ–функции, а обратное преобразование Фурье от постоянной функции F(z) = c равно δ–функции с коэффициентом c .
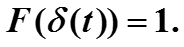
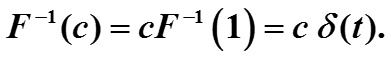
4.3. Фурье-преобразование некоторых функции
Нам понадобится преобразование Фурье от экспоненты в мнимой степени
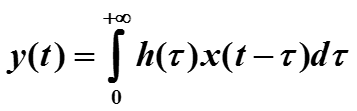
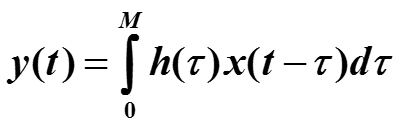
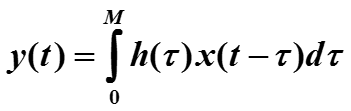
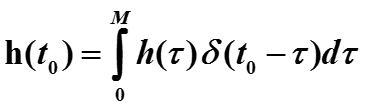
