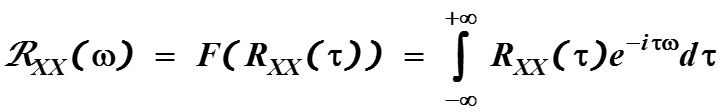- Процесс случайного блуждания не эргодический, так как он нестационарный.
-
Пример. Телеграфный сигнал – эргодический процесс, так как
-
1) он стационарный,
-
2) для него выполняется условие Слуцкого
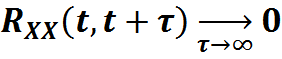
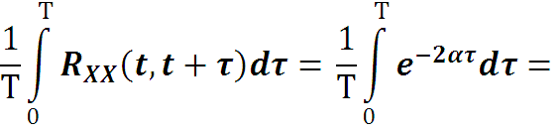
Page 8
8.1. Эргодические случайные процессы
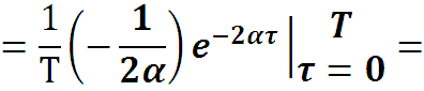
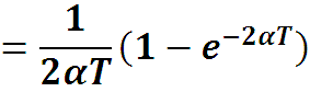
-
Так как α > 0 , то выражение в скобках при T→∞ стремится к 1, а множитель перед скобкой стремится к 0 ,
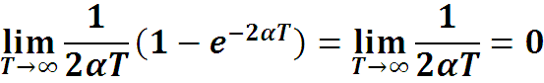

Page 9
8.1. Эргодические случайные процессы
-
Пример. Гауссовский некоррелированный процесс X(t) (то есть случайными величинами X(t1) и X(t2) некоррели-рованы) эргодический, так как он
-
1) стационарный,
-
2) выполняется условие Слуцкого

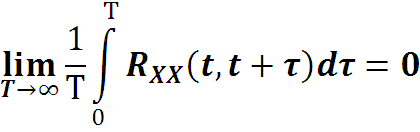


Page 10
8.2. Свойства функции автоковариации
1. Функция автоковариации не изменяется при перестановке аргументов:
RXX(t1, t2) = RXX(t2, t1) . Эти следует из равенства
2. При умножении случайного процесса X(t) на постоянное значение с значения функции автоковариации увеличи-ваются в с2 раз.
3. При умножении случайного процесса X(t) на неслучайную функцию f(t) автоковариация увеличивается в f(t1) f(t2) раз.
4. Функция автоковариации стационарного процесса зависит только от разности времени τ= t2 - t1:
RXX(t1, t2) = RXX(t, t+τ) = RXX(τ).
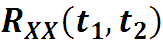
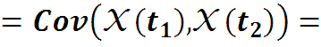
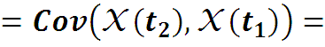
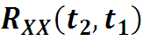
Page 11
8.2. Свойства функции автоковариации
Это следует из того, что в стационарном процессе для любого момента времени t совместные распределения от аргументов t, t+τ совпадают. Ввиду этого свойства функция автоковариации стационарного процесса записывается в виде RXX(τ).
5. Для стационарного процесса RXX(0) ≥ RXX(τ).
Это следует из того, что математическое ожидание неотрицательной величины
Добавим в скобки +m и –m , обозначим , тогда ввиду неотрицательности мат ожидания неотрица-тельной величины
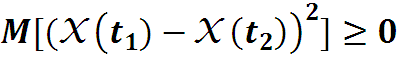
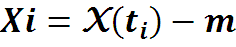
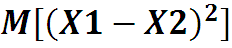
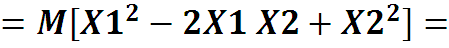
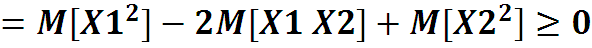
Page 12
8.2. Свойства функции автоковариации
Отсюда
Но процесс X(t) стационарный, поэтому
(дисперсия стационарного процесса не зависит от момента времени t). Тогда
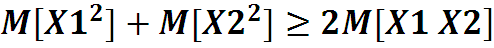
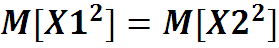
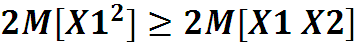
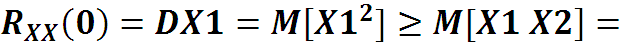
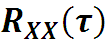
Это свойство подтверждает ясный по смыслу факт, что наибольшая взаимосвязь в стационарном сигнале наблюдается при t1 = t2, (τ=0) это очевидно, так как со временем зависимость сигнала от того, что было в прошлом ослабевает.
Page 13
8.2. Свойства функции автоковариации
График автоковариации телеграфного сигнала для α=1, τ ϵ[-∞, +∞], автоковариация RXX(τ) = exp(-2α | τ |) (функция автоковариации четная для любого стационарного процесса) .
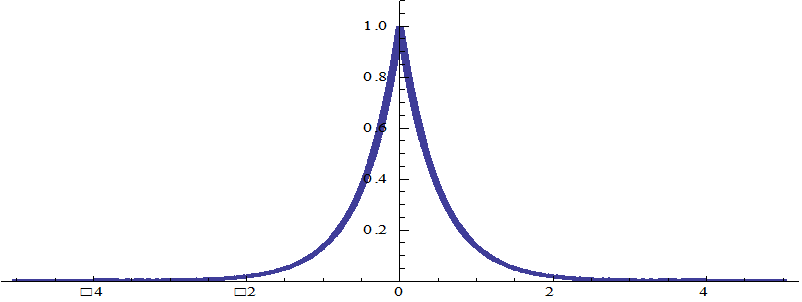
Процесс называется некоррелированным, если при t1 ≠ t2 его функция автоковариации RXX(t1 ,t2) = 0 .
Page 14
8.2. Свойства функции автоковариации
-
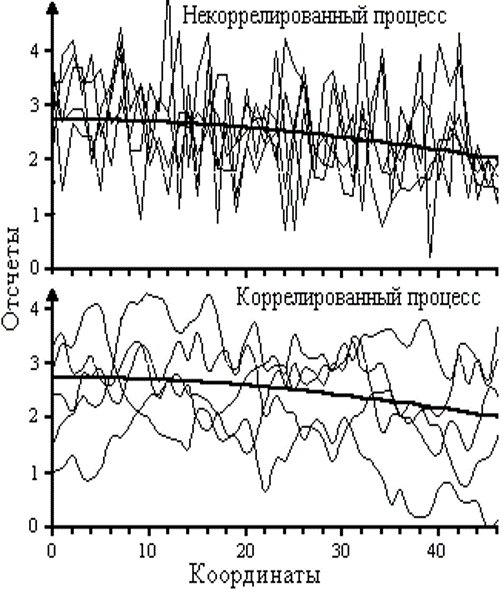
Некоррелированный и коррелированный процессы.
-
Ансамбли из 5 реализаций некоррелированного и коррелированного процессов.
-
На рисунке приведены примеры реализаций двух случайных процессов, которые имеют одно и то же математическое ожидание и дисперсию для случайных величин X(t) с фиксированным временем t.
Page 15
8.2. Свойства функции автоковариации
-
Пространство состояний (значения) обоих процессов практически одно и то же, но динамика развития процессов в реализациях существенно различается.
-
Единичные реализации коррелированных процессов в произвольный момент времени t могут быть такими же случайными, как и некоррелированных, во всех сечениях оба процесса могут иметь один и тот же закон распределения случайных величин.
-
Однако динамика развития по времени t единичной реализации коррелированного процесса по сравнению с некоррелированным является более плавной, в коррелированном процессе имеется некоторая связь между последовательными значениями случайных величин, то есть величины в различные моменты времени взаимосвязаны.
Page 16
8.2. Свойства функции автоковариации
-
Оценку степени зависимости случайных величин X(t1) и X(t2) (мгновенные значений процесса X(t) ) в произвольные моменты времени t1 и t2 выполняет функция автоковариации RXX (t1,t2 ).
Page 17
8.3. Спектральная функции мощности
-
Случайный процесс X(t) - это совокупность случайных величин, зависящих от времени t.
-
Стационарные случайные процессы аналогично вещест-венным функциям, которые разлагаются в ряд Тейлора, допускают разложение в другие (обычно более простые) случайные процессы, в том числе и ортогональные – это упрощает разложение.
-
При анализе случайного сигнала часто используются моменты второго порядка – автоковариационную и автокорреляционную функции и их Фурье-образы.
-
Автокорреляционной функцией случайного процесса X(t) называется
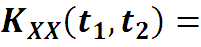
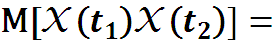
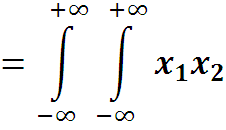
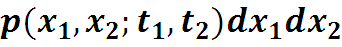
Page 18
8.3. Спектральная функции мощности
-
Автокорреляционная функция стационарного случайного процесса зависит от разности и записывается в виде
-
Автокорреляционная функция сохраняет все свойства автоковариационной функции, в частности, она четная,
-
Автокорреляционная функция стационарного процесса отличается от автоковариационной функции на посто-янную величину: (только для стационарного процесса).
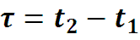
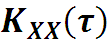
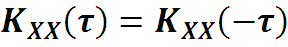
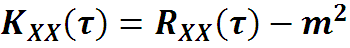
-
Автокорреляционная и автоковариационная функции – это детерминированные функции вещественного аргумента со значениями в вещественной области.
Page 19
8.3. Спектральная функции мощности
-
К этим функциям можно применить преобразование Фурье Фурье-образ автокорреляционной функции позволяет оценить энергию случайного сигнала в частотном диапа-зоне. Для автоковариационной функции RXX(τ) положим
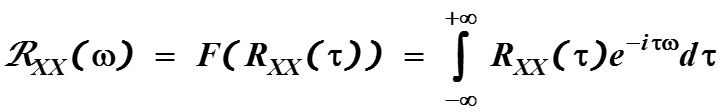
-
Для автокорреляционной функции KXX(τ) преобразование Фурье имеет
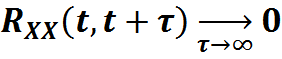
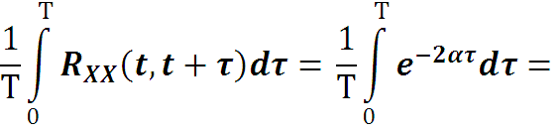
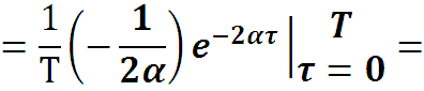
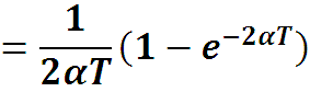
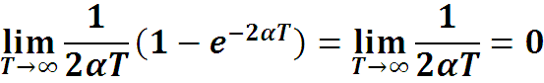


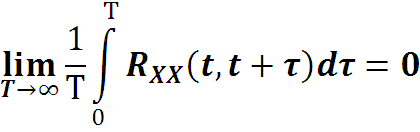


![]()
![]()
![]()
![]()
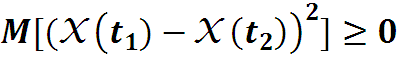
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
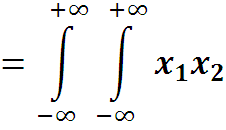
![]()
![]()
![]()
![]()
![]()