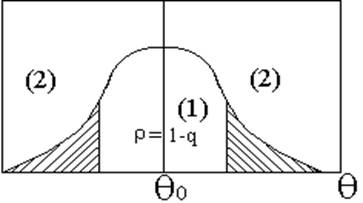
Электротехника \ Элементная база радиоэлектронных средств

Анализ статистических параметров радиоэлементов массового производства: Методические указания к выполнению лабораторной работы № 1 по курсу "Элементная база РЭС", страница 14

Рисунок 2 - Области принятия гипотезы (1) и критическая область (2) для двустороннего критерия.

Если же при нулевой гипотезе Н₀: q=q₀ альтернативная гипотеза Н₁ формулируется как Н₁: q>q₀ или Н₁: q<q₀, то соответствующие критерии называются односторонними и их критические области содержат всего одну зону (рисунок 3).

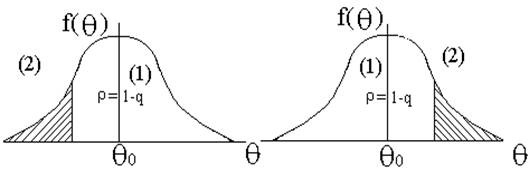
Рисунок 3 - Область принятия гипотезы (1) и критическая область (2) для одностороннего критерия: а- Н₁: q<q₀, б- Н₁: q>q₀.

Приложение Е

c² - РАСПРЕДЕЛЕНИЕ

Значение c² в зависимости от числа степеней свободы и вероятностей a: Р{c²>c²_n_,_a}=a


n	Вероятность		n	Вероятность		n	Вероятность
	0,975	0,025		0.0975	0.025		0.975	0.025
1	0,00098	5,0	11	3.8	21.9	21	10.3	35.5
2	0,051	7,4	12	4.4	23.3	22	11.0	36.8
3	0,210	9,3	13	5.0	24.7	23	11.7	38.1
4	0,48	11,1	14	5.6	26.1	24	12.4	39.4
5	0,83	12,8	15	6.3	27.5	25	13.1	40.6
6	1,24	14,4	16	6.9	28.8	26	13.8	41.9
7	1,69	16,0	17	7.6	30.2	27	14.6	43.2
8	2,18	17,5	18	8.2	30.5	28	15.3	44.5
9	2,70	19,0	19	8.9	32.9	29	16.0	45.7
10	3,25	2	20	9.6	34.2	30	16.8	47.0
30

ПРИЛОЖЕНИЕ Ж

НОРМИРОВАННОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Значение U_a в зависимости от вероятности a:Р{U>U_a}=a

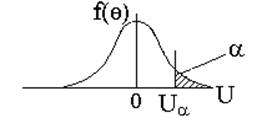
a	0.20	0.10	0.05	0.025	0.01	0.005	0.001	0.0005
U	0.84	1.28	1.64	1.96	2.33	2.58	3.09	3.29

ПРИЛОЖЕНИЕ З

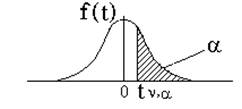
t - РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА

Значения t_n_,_a в зависимости от числа степеней свободы n и вероятности a: Р{t> t_n_,_a}=a

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Скачать файл