Анализ статистических параметров радиоэлементов массового производства: Методические указания к выполнению лабораторной работы № 1 по курсу "Элементная база РЭС", страница 13

На практике наиболее часто используют уровень значимости q=0.05. При любом постоянном объёме выборки N вероятность совершить ошибку первого рода можно снизить, уменьшая уровень значимости q, однако при этом возрастает вероятность допустить ошибку второго рода.

Наиболее употребительные критерии для проверки различных гипотез, касающихся значений математического ожидания, дисперсии и коэффициента корреляции, разработаны в предложении, что выполняются следующие условия:

1)   выборки являются случайными, с независимыми наблюдениями;

2)   исследуемые совокупности имеют нормальное распределение.

Поэтому первым эталоном проведения статистического анализа является проверка закона распределения исследуемой случайной величины на соответствие нормальному закону распределения. Если закон распределения можно считать нормальным, то проверка статистических гипотез сводится к выполнению следующих этапов:

1)   выдвижение нулевой гипотезы Н₀;

2)   определение альтернативной гипотезы Н₁;

3)   выбор подходящей статистики g для проверки гипотез;

4)   установление критической области для проверки гипотезы Н₀ с учётом альтернативной гипотезы Н₁ и уровня значимости q;

5)   вычисление значения статистики g и принятия решения: если статистика попала в область принятия гипотезы Н₀, то гипотеза Н₀ считается справедливой; если же статистика оказалась в критической области, то гипотеза Н₀ отвергается.

ПРИЛОЖЕНИЕ Д

ПРОВЕРКА  СТАТИСТИЧЕСКИХ  ГИПОТЕЗ

Ответственным этапом является проверка гипотезы о соответствии закона распределения нормальному. Для качественного анализа и наглядности полезно построить графики гистограммы и отвечающего параметрам выборки нормального закона распределения. Для построения гистограммы используют формулы (4)-(6). По оси абсцисс (рисунок 1), соответствующей значениям случайной величины, откладывают границы каждого из К интервалов и для каждого интервала строят прямоугольники с высотой, равной эмпирической вероятности P^*_j. Теоретические вероятности P_j, необходимые для построения графика аппроксимирующего нормального закона распределения, рассчитывают по формуле (2), приняв в качестве функции j(х) функцию нормального распределенияи s{x}=S{x}

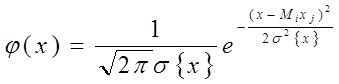     .            (22)

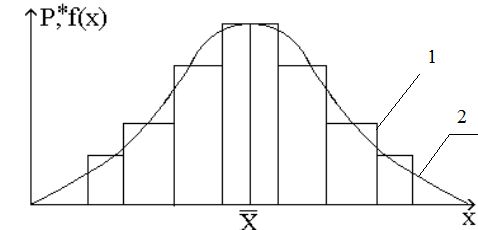
Рисунок 1 - Гистограмма (1) и график нормального распределения (2)

Количественно гипотеза о соответствии закона распределения случайной величины нормальному закону распределения проверяется несколькими способами. Одним из наиболее эффективных является способ на основании c²- критерия, расчётное значение которого вычисляется по формуле

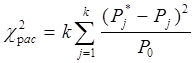                .                  (23)

Для проверки гипотезы необходимо сравнить расчётное значение c²_рас с его критическим значением c²_кр, которое находится из таблицы c²-распределения для n=k-2 числа степеней свободы при вероятности a=q. Если c²_рас<c²_кр, следовательно, этот критерий не противоречит гипотезе о нормальности распределения. Если закон распределения нормальный, то представляется возможным эффективно использовать оценки и S{x} для проверки гипотез о равенстве выборочного среднего математическому ожиданию, о равенстве оценки S{x} стандартному отклонению, о значимости выборочного коэффициента корреляции. Проведение анализа зависит от характера альтернативной гипотезы Н₁, противопоставляемой нулевой гипотезе Н₀. Если нулевой гипотезе Н₀:q=q₀ противопоставляется альтернативная гипотеза Н₁:q¹q_0, где q- значение оцениваемого параметра, а q₀ - его значение в генеральной совокупности, то критерий для проверки Н₀ носит название двустороннего, а его критическая область состоит из двух частей  (рисунок 2). Как правило, границы критической области выбираются таким образом, чтобы вероятность попадания в левую и правую части критической области была бы одинакова (a=q/2).