Анализ статистических параметров радиоэлементов массового производства: Методические указания к выполнению лабораторной работы № 1 по курсу "Элементная база РЭС", страница 11

На практике часто используют дифференциальную форму закона распределения, как более наглядную. Дифференциальная функция распределения, или функция плотности вероятности случайной величины, j(х)- это производная от интегральной функции распределения

                                                .                       (1)

Функция всегда положительна, стремится к нулю при êх÷®¥, площадь под кривой j(х), т.е. ,равна единице.

Для вычисления вероятности нахождения случайной величины внутри любой части из области её возможных значений нужно воспользоваться формулой

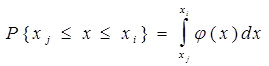,         (2)

где(х_i - x_j) - интервал, внутри которого определяют вероятность нахождения случайной величины x.

Если известна функция F(x), то аналогичные вычисления можно выполнить по формуле

                .                         (3)

Формулу (3) используют для определения вероятностей нормального закона распределения при использовании табулированных значений функции F(x).

Для построения эмпирического графика функции j(х) - гистограммы - строят ряд распределений эмпирических вероятностей (вариационный статистический ряд), в котором границы возможных значений функции j(х) определяет интервал, ограниченный максимальным x_max и минимальным x_min значениями случайной величины в выборке. Этот интервал разбивают на k частей, ширину каждой части определяют по формуле

.                            (4)

Количество интервалов k рассчитывают приближённо по формуле

                              (5)

округляя результат до ближайшего целого.

Вероятность Р^*_j попадания случайной величины в интервал (х_j+1-x_j) равна относительной частоте n_j, которую определяют по формуле

                                                         (6)

где N_j - количество дискретных значений случайной величины, попадающих в данный интервал; N - объём выборки.

При неограниченном объёме выборки N эмпирическая вероятность стремиться к теоретической, т.е. справедливо

                           при N=¥.                           (7)

Для интерполяции гистограммы теоретическим законом распределения используют выборочные оценки математического ожидания и дисперсии. Оценкой математического ожидания служит среднее значение случайной величины, которое рассчитывается по данным вариационного ряда по формуле

                                                          (8)

или по непосредственным данным выборки

                                                         (9)

где  - выборочное среднее значение случайной величины, являющееся оценкой её математического ожидания; х_j - компонента вариационного ряда; n_j - относительная частота для j-го интервала; k - количество членов вариационного ряда (количество интервалов гистограммы); N - объём выборки; x_i - i-я компонента выборки.

При неограниченном возрастании объёма выборки N оценка  стремится к математическому ожиданию случайной величины, т.е. 

                    при  N®¥.                           (10)

Оценкой дисперсии дискретной случайной величины S²{x} является математическое ожидание квадрата отклонений этой величины от центра её распределения, которое при известном математическом ожидании по данным вариационного ряда рассчитывают по формуле

                                 (11)

или непосредственно по данным выборки - по формуле

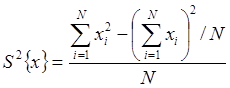                             (12)

Если значение параметра М{x} не известно, то при расчётах используют формулы

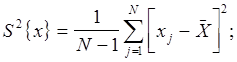                              (13)

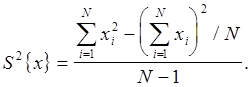                               (14)

При неограниченном возрастании объёма выборки N оценка S²{x} стремится к дисперсии s²{x}, т.е. справедливо

           при N®¥.                  (15)

Величину  называют среднеквадратичным или стандартным отклонением.