Анализ статистических параметров радиоэлементов массового производства: Методические указания к выполнению лабораторной работы № 1 по курсу "Элементная база РЭС", страница 12

Математическое ожидание М{x} и дисперсия s²{x} являются наиболее употребительными числовыми характеристиками случайной величины. Они полностью определяют одну из наиболее важных функций распределения, а именно нормальное распределение. Однако и для других распределений эти характеристики дают возможность в первом приближении оценить характер функции распределения и указывают центр рассеяния случайной величины и степень рассеяния.

Если необходимо определить наличие статистической связи между двумя случайными величинами X и Y, то для этого используют коэффициент взаимной корреляции. Оценка коэффициента корреляции r{x,y}, которая также является случайной величиной и зависит от объёма выборки N, рассчитывается по формуле

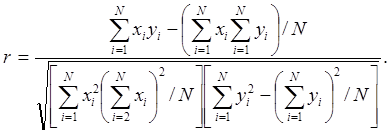         (16)

Оценки  и S² являются случайными величинами. При нормальном законе распределения случайной величины законы распределения этих оценок отвечают определённым функциям - статистикам, которые используют для проверки статистических гипотез. Параметры функций статистик зависят от объёма выборки N.

Статистика оценки  при известном значении параметра s²{x} отвечает нормальному закону распределения с дисперсией

                 .                 (17)

Если дисперсия s²{x} не известна, то статистика  отвечает t- распределение Стьюдента с n=N-1 степенями свободы.

Для проверки статистических гипотез используют нормированные значения оценок s²{x} и s²{}

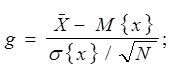                                       (18)

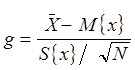                          .                           (19)

Нормированная дисперсия s²{x} оценка S²{x} отвечает c²- распределению с n=N степенями свободы при известном значении параметра М{x} и n=N-1степенями свободы при неизвестном параметре М{x}. Для проверки статистических гипотез о дисперсии случайной величины используют статистики:

                       ,                         (20)

если М{x} известно, и

                         ,                      (21)

если М{x} неизвестно.

Точное распределение выборочного коэффициента корреляции весьма сложно. При проверке значимости этого коэффициента на практике удобно пользоваться специальными таблицами, в которых приведены его критические значения в зависимости от объёма выборки N.

Определяющее практическое значение имеет проверка статистических гипотез, другими словами, определённых предложений относительно свойств генеральной совокупности, из которой извлекается выборка.

Статистические гипотезы проверяются по правилам-критериям, которые позволяют отвергнуть или принять данную гипотезу на основании выборки. При построении такого правила используют функции-статистики результатов наблюдений, значения которых вычисляют по формулам (13)-(21).

Все возможные значения функций-статистик для проверки той или иной гипотезы делятся на две части: область принятия гипотезы и критическую область. Критическая область состоит из всех значений статистики, при которых принимается решение отвергнуть проверяемую гипотезу как ложную. Проверка гипотезы сводится к выяснению, попадает или нет значение используемой статистики в критическую область: если нет, гипотеза принимается как не противоречащая результатам наблюдений, если да, гипотеза отвергается. Так как эти решения базируются на статистиках, найденных по выборкам ограниченного объёма, то при выборке решения всегда возможны ошибки (таблица 1).

Вероятность совершить ошибку первого рода, т.е. отвергнуть правильную гипотезу, называется уровнем значимости критерия и обозначается буквой q. Вероятность ошибки второго рода, т.е. вероятность принять неверную гипотезу, обозначается буквой b.

ТАБЛИЦА 1 Типы ошибок при проверке статистических гипотез