|
Ряды |
||
|
числовые |
функциональные |
|
|
Знакопостоянные |
Знакопеременные |
Степенные (ряды Тейлора и Маклорена) |
|
1) необходимый признак
|
1) исследование на абсолютную сходимость по необходимому признаку |
Ряды Фурье |
|
2) достаточные признаки (признак Деламбера)
|
2) если абсолютной сходимости нет, то на условную сходимость по признаку Лейбница
|
Просто функциональные |
|
3) Радикальный признак Каши
|
||
|
4) интегральный признак Каши
Из сходимости интеграла следует сходимость ряда. Из расходимости интеграла следует расходимость ряда. |
||
|
5) Признак сравнения
Если |
||
Ряды Фурье
![]()
![]() -
простая гармоника
-
простая гармоника
![]() -
пространство непрерывных на
-
пространство непрерывных на ![]() функций
функций
![]()
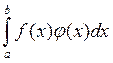 -
действительное пространство
-
действительное пространство
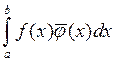 - в
комплексном случае
- в
комплексном случае
Определение: Функции ![]() и
и ![]() называются
ортогональными, если их скалярное произведение равно нулю.
называются
ортогональными, если их скалярное произведение равно нулю.
Системы функций
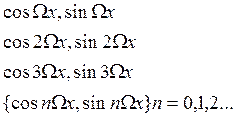 (1)
(1)
имеют общий период ![]()
Теорема: Тригонометрические функции системы (1) попарно ортогональны на любом отрезке длиной Т .
Доказательство: ![]()
![]()
![]()
![]()
1) ![]()
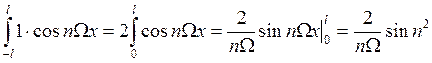
2) ![]()
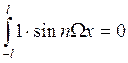
3) ![]()
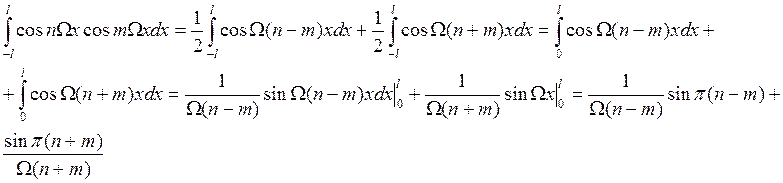 4)
4) ![]()
……………………
5) ![]()
……………………
Пусть ![]() -
периодическая с периодом Т функция
-
периодическая с периодом Т функция
![]() (1)
(1)
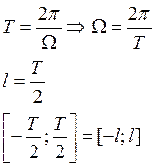
Пусть ряд (1) сходится
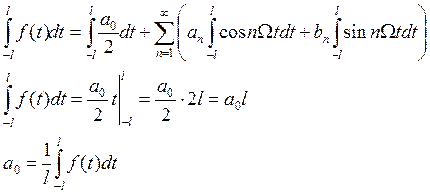
Умножим обе части равенства (1)
на ![]() и проинтегрируем на
и проинтегрируем на ![]()
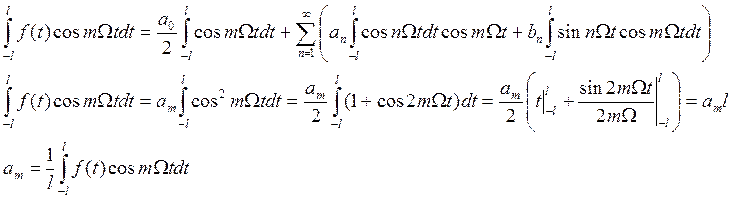
Умножим обе части равенства (1)
на ![]() и проинтегрируем:
и проинтегрируем:
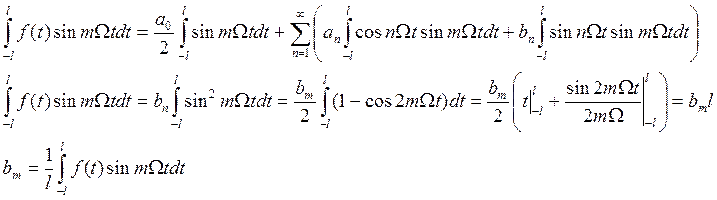
Определение: числа ![]() - называются коэффициента Фурье, а ряд
(1) – рядом Фурье функции
- называются коэффициента Фурье, а ряд
(1) – рядом Фурье функции ![]() .
.
Теорема: Пусть переодическая с
периодом Т функция ![]() определена на всей числовой
оси, кусочно монотонна и ограничена, тогда ее ряд Фурье сходится для любого t, причем в точке непрерывности сумма ряда
определена на всей числовой
оси, кусочно монотонна и ограничена, тогда ее ряд Фурье сходится для любого t, причем в точке непрерывности сумма ряда ![]() , а в точке разрыва
, а в точке разрыва ![]() .
.
Частный случай: пусть ![]() ,
тогда
,
тогда
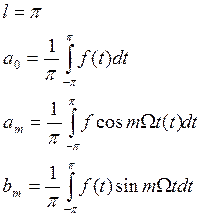
Замечание: в формулах для ![]() вместо
промежутка интегрирования
вместо
промежутка интегрирования ![]() можно поставить любой
промежуток от
можно поставить любой
промежуток от ![]() до
до ![]() .
.
![]()
![]()
![]()
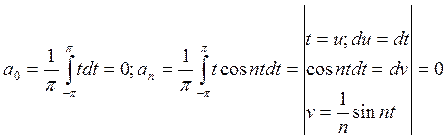
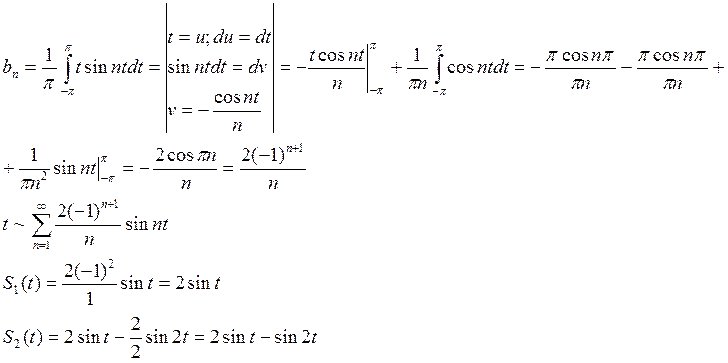
Ряды Фурье четных и нечетных функций
1) Предположим, что ![]() - четная, т.е.
- четная, т.е. ![]()
![]()
![]() .
.
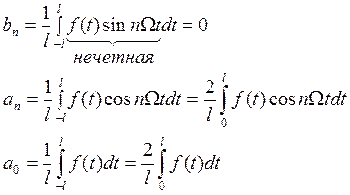
2) ![]() - нечетная
- нечетная
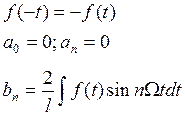
Замечание: Четная функция раскладывается в ряд Фурье по косинусу, а нечетная по синусу.
Ряды Фурье для функций заданных на полупериоде
![]()
Вместо функции f(t) рассматривают функцию F(t)
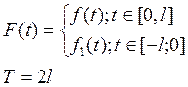
F(t) можно разложить в ряд Фурье на отрезке [-l,l], т.к. ![]() на отрезке
на отрезке ![]()
1) Нечетным образом, следовательно раскладывается на ряд Фурье по синусу.
2) Или четным образом, следовательно раскладывается на ряд Фурье по косинусу.
3) Любым другим способом.
Гармоники
![]() -
гармонические колебания
-
гармонические колебания
S – отклонение точки от положения равновесия
А – амплитуда колебаний
![]() -
частота
-
частота
![]() -
начальная фаза
-
начальная фаза
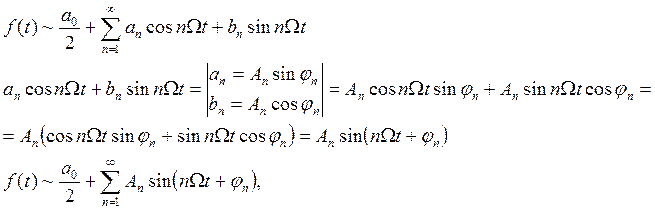
где ![]() ,
,
![]()
Совокупность чисел ![]() называется амплитудным спектром сигнала,
называется амплитудным спектром сигнала,
![]() - частотным спектром.
- частотным спектром.
Комплексная форма ряда Фурье
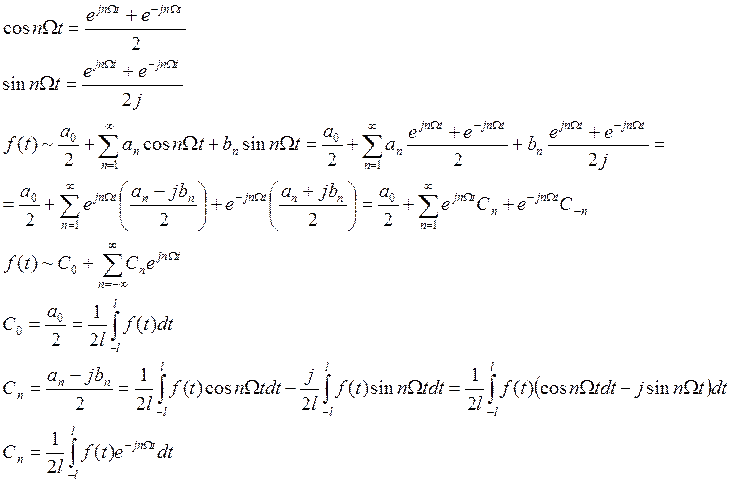
Если функция ![]() действительная, то числа
действительная, то числа ![]() и
и ![]() действительные
и
действительные
и ![]() .
.
n-ная
частичная сумма ряда ![]() , записывается в виде
, записывается в виде ![]() .
.
Ряд сходится для данного значения
t, если существует предел ![]() .
.
Введенная таким образом сходимость называется сходимостью в смысле главного значения.
Если ![]() -
четная, то
-
четная, то ![]() =0,
=0, ![]() ,
т.е. число
,
т.е. число ![]() - чисто действительное число.
- чисто действительное число.
Если ![]() -
нечетная, то
-
нечетная, то ![]() и
и ![]() равны
нулю,
равны
нулю, ![]() , т.е.
, т.е. ![]() -
чисто мнимое число.
-
чисто мнимое число.
Если ![]() функция
общего вида, то в
функция
общего вида, то в ![]() есть и действительная и мнимая
часть.
есть и действительная и мнимая
часть.
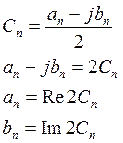
Комплексные функции ![]() ,
, ![]() образуют
ортогональную систему функций на отрезке [-l,l], т.к.
образуют
ортогональную систему функций на отрезке [-l,l], т.к.
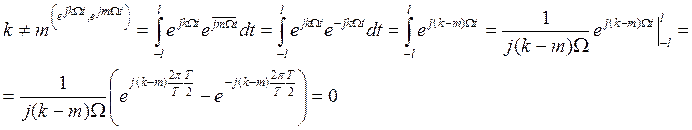
Последовательность ![]() , называется комплексным спектром
функции.
, называется комплексным спектром
функции.
Интеграл Фурье
1) ![]() ,
следовательно она раскладывается в ряд Фурье обычно (или комплексно)
,
следовательно она раскладывается в ряд Фурье обычно (или комплексно)
2) ![]() задана
на отрезке [-l,l]
задана
на отрезке [-l,l]
3) ![]() задана
на всей числовой прямой и не периодическая
задана
на всей числовой прямой и не периодическая
Пусть функция ![]() определена на всей числовой оси,
кусочномонотонна, ограничена и абсолютно интегрируема
определена на всей числовой оси,
кусочномонотонна, ограничена и абсолютно интегрируема 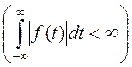 .
.
Устремим период ![]()
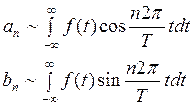
Выражение ![]()
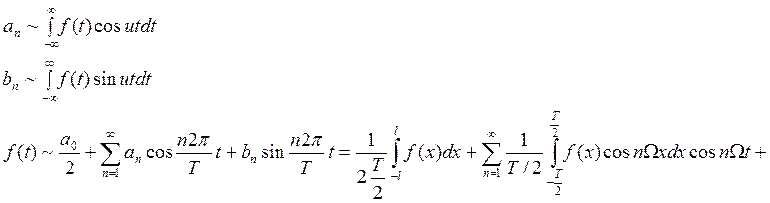
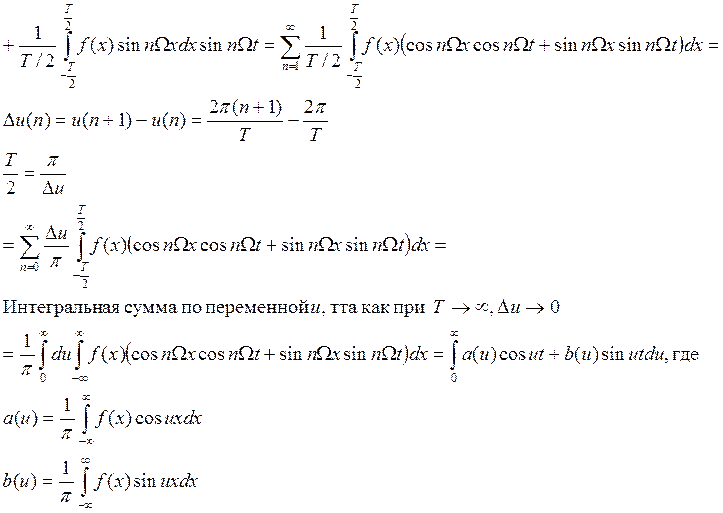
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.