Интеграл берется выделением полного квадрата и в зависимости от знака «а» сведением к табличным интегралам (12), (13), (14).
Пример:
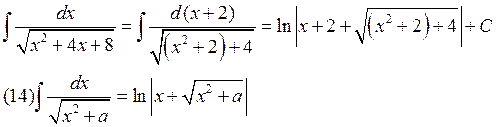
IV. 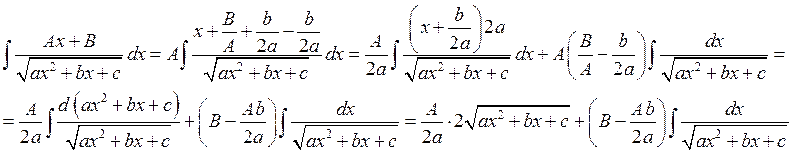
Интегрирование дробей.
1) Интегрирование простых дробей.
Определение: Простыми дробями I – IV типов называется дроби вида:
I. ![]()
II.![]()
III. ![]() ,
, ![]()
IV. 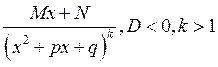
1) ![]()
2) 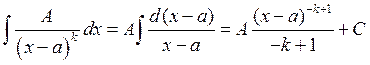
3) 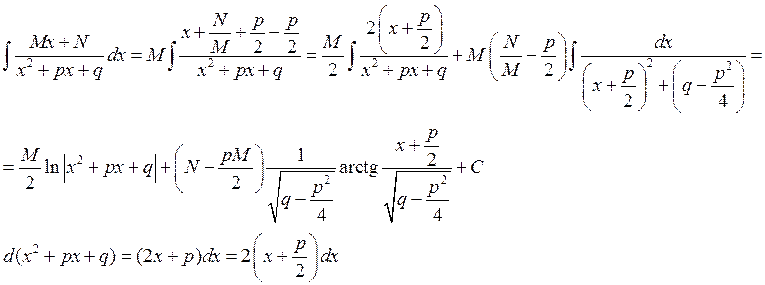
Интегрирование рациональных дробей.
Теорема 1:
Если знаменатель правильной рациональной не сократимой дроби ![]() имеет действительный корень
имеет действительный корень ![]() , т.е.
, т.е. ![]() , причем
, причем
![]() , то дробь представима в виде суммы двух
правильных дробей
, то дробь представима в виде суммы двух
правильных дробей ![]() .
.![]() и
степень
и
степень ![]() меньше степени знаменатель второго
слагаемого.
меньше степени знаменатель второго
слагаемого.
Доказательство:
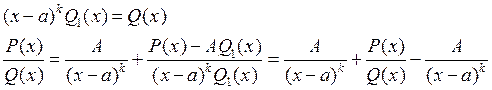
Подберем А
так, чтобы число ![]() было корнем второй дроби.
было корнем второй дроби.
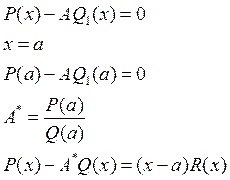
![]()
Замечание: Поскольку второе слагаемое также правильная рациональная не сократимая дробь, то его можно разложить с использованием этой теоремы:
![]()
Процесс
выделения простой дроби продолжается до тех пор пока знаменатель не будет
равным ![]() .
.
![]()
Замечание:
Если знаменатель правильной рациональной не сократимой дроби имеет вид ![]() , то дробь
, то дробь ![]() представима
в виде:
представима
в виде:
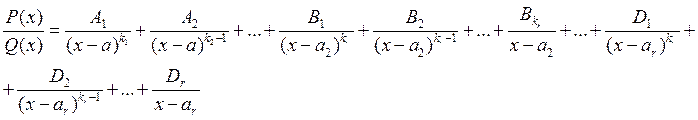
Пример:
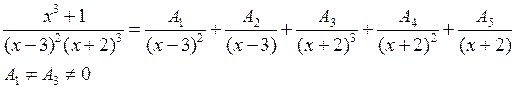
Теорема 2:
Если знаменатель правильной рациональной не сократимой дроби ![]() , где
, где ![]() имеет
комплексно сопряженные корни
имеет
комплексно сопряженные корни ![]() кратности
кратности ![]() , и
, и ![]() , то
эту дробь можно представить в виде суммы двух правильных дробей
, то
эту дробь можно представить в виде суммы двух правильных дробей
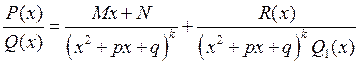 , где
, где ![]() -
константы не равные нулю одновременно,
-
константы не равные нулю одновременно, ![]() -
многочлен.
-
многочлен.
Так как второе
слагаемое также является правильной рациональной не сократимой дробью, то из
второй дроби можно выделить еще одну простейшую и т.д. , до тех пор пока не
останется дробь ![]() .
.
Вывод: Любая рациональная правильная не сократимая дробь может быть представлена виде суммы простейших дробей I-IV типа с помощью теорем 1 и 2.
Пример:
![]()
Для вычисления коэффициента необходимо:
I. Сравнение коэффициентов при одинаковых степенях.
1) Привести дроби в правой части разложения к общему знаменателю и записать в числитель получившийся многочлен с неизвестными коэффициентами.
![]()
![]() - многочлен с неизвестными
коэффициентами.
- многочлен с неизвестными
коэффициентами.
2) Так
как знаменатели дробей одинаковы, то одинаковыми должны быть и числители. ![]() (*)
(*)
3) Многочлены равны когда, когда равны коэффициенты при одинаковых степенях, т.е.
![]()
можно показать, что такая система всегда имеет единственное решение.
4) Решив систему находят числовые значения неизвестных коэффициентов и подставляют полученные числа в разложение.
II. Метод частных значений.
1) Привести дроби в правой части разложения к общему знаменателю и записать в числитель получившийся многочлен с неизвестными коэффициентами.
![]()
![]() - многочлен с неизвестными
коэффициентами.
- многочлен с неизвестными
коэффициентами.
2) Так как
знаменатели дробей одинаковы, то одинаковыми должны быть и числители. ![]() (*)
(*)
3) Если (*)
выполняется, то значение многочленов ![]() и
и ![]() при одинаковых числовых значениях
при одинаковых числовых значениях ![]() должны быть равными, поэтому взяв вместо
должны быть равными, поэтому взяв вместо
![]() разные числа и подставить их в (*) можно
также получить уравнения для неизвестных коэффициентов.
разные числа и подставить их в (*) можно
также получить уравнения для неизвестных коэффициентов.
Вместо ![]() берут значения совпадающие с
действительными корнями знаменателя.
берут значения совпадающие с
действительными корнями знаменателя.
III. Комбинированный метод.
Чаще используется комбинированный метод, когда часть уравнений получается приравниванием коэффициентов остальные методом частичных значений.
Пример:
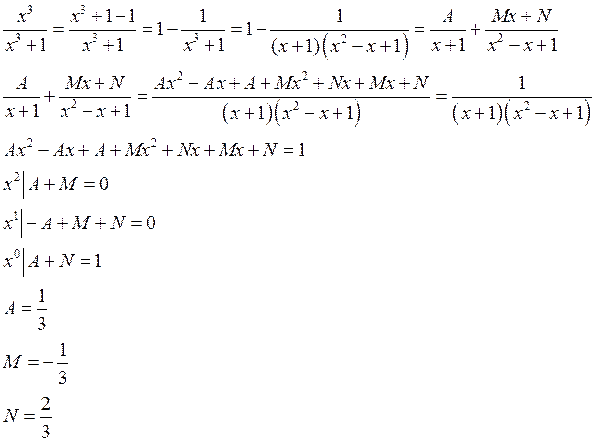
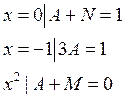
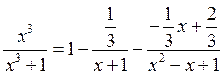
Метод
частичных значений предпочтительнее в случае, когда корни знаменателя
действительные и простые, при этом скобки в многочлене ![]() с
неизвестными коэффициентами раскрывать ненужно.
с
неизвестными коэффициентами раскрывать ненужно.
Алгоритм интегрирования рациональных дробей.
1) Представить неправильную дробь в виде суммы многочлена и правильной дроби.
2) Найти корни знаменателя и разложить его на множители.
3) Разложить правильную дробь на простейшие и найти неизвестные коэффициенты.
4) Проинтегрировать простые дроби.
Пример:
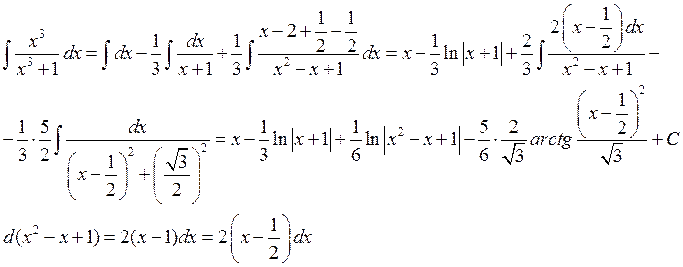
Интегрирование тригонометрических выражений.
![]() , где
, где ![]() -
рациональная функция от
-
рациональная функция от ![]() и
и ![]() .
.
1) ![]() (универсальная тригонометрическая
подстановка). Покажем, что такой интеграл подстановочный и сводится к интегралу
(универсальная тригонометрическая
подстановка). Покажем, что такой интеграл подстановочный и сводится к интегралу
![]()
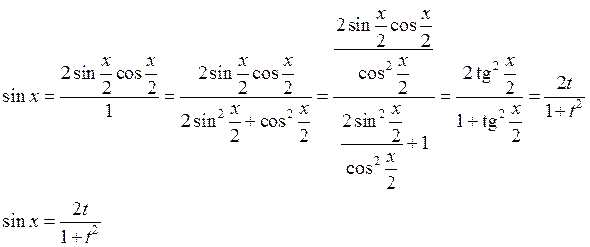
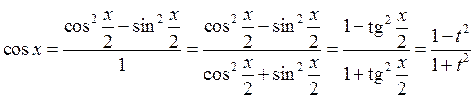
![]()
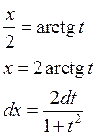
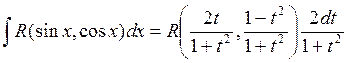
Пример:
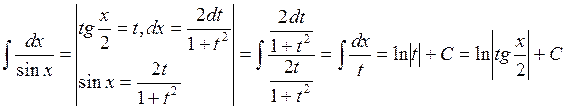
2) Подынтегральная функция четна по синусу и косинусу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.