Пусть кривая задана в параметрической форме
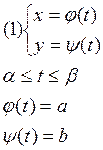
Пусть уравнения (1) определяют некоторую кривую y=f(x) на отрезке [a,b]. Тогда площадь можно вычислить по формуле
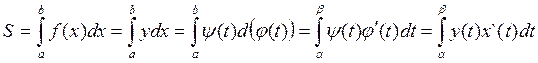
Пример:
![]()
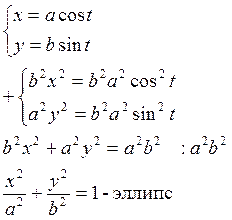
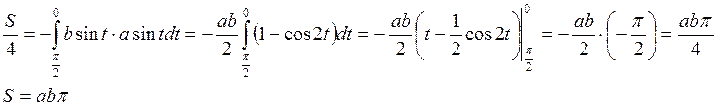
3) Площадь фигуры заданной в полярных координатах.
Пусть есть полярная система
координат. Кривая задана уравнением ![]() , где
, где ![]() - непрерывная функция при
- непрерывная функция при ![]() .
.
Найти площадь сектора AOB, ограниченного кривой ![]() и
лучами
и
лучами ![]() и
и ![]() .
.
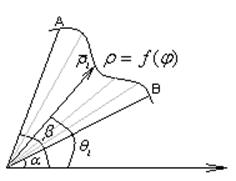
Разобьем площадь радиус-векторами
![]() .
.
![]()
![]() -
длина радиус-вектора соответствующего углу
-
длина радиус-вектора соответствующего углу ![]() ,
тогда площадь сектора с радиусом
,
тогда площадь сектора с радиусом ![]() и углом
и углом ![]() вычисляется по формуле:
вычисляется по формуле:
![]()
Сложив элементарные площади
получим ![]() .
.
Последнее равенство есть
интегральная сумма для функции![]() на отрезке
на отрезке ![]() ,
, 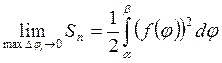 .
.
Пример: Найти площадь фигуры
ограниченной вторым витком спирали Архимеда (![]() )
)
![]()
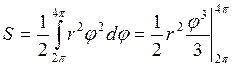
4) Длина дуги кривой в декартовой системе координат.
Задана кривая y=f(x). Найти длину дуги кривой заключенной между вертикальными прямыми х=а, х=b.
![]() Возьмем на дуге точки А, М1,
М2, …,Мi, В с абсциссами а, х1, х2,
…, хi, b и проведем
хорды АМ1, М1М2, …, длины которых
соответственно
Возьмем на дуге точки А, М1,
М2, …,Мi, В с абсциссами а, х1, х2,
…, хi, b и проведем
хорды АМ1, М1М2, …, длины которых
соответственно ![]() … .
… .
Хорда ![]() вписана
в хорду АВ.
вписана
в хорду АВ.
![]() .
.
Докажем, что если на отрезке [a,b] функции y=f(x) и y=f`(x) непрерывны, то этот предел
существует, пусть ![]()
По теореме Пифагора:
По теореме Лагранжа:
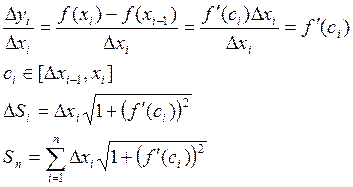
Так как функция f `(x) непрерывна, то функция ![]() тоже непрерывна и существует
тоже непрерывна и существует ![]() , который равен
, который равен 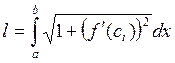 -
длина линий в декартовых координатах.
-
длина линий в декартовых координатах.
Пример: Вычислить длину
окружности ![]() .
.
![]()
![]()
следовательно ![]()
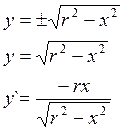
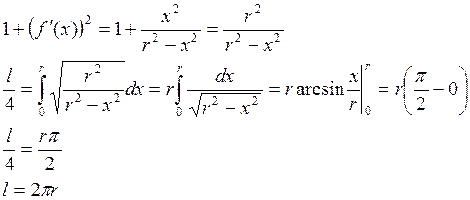
5) Длина линии, если кривая задана параметрически.
![]()
![]() , где
, где ![]() и
и ![]() непрерывные
на
непрерывные
на ![]() функции.
функции.
![]() и
и ![]() , также непрерывны на
, также непрерывны на ![]() и
и ![]() ,
тогда система (1) определяет кривую y=f(x), где f(x)
непрерывна, f `(x) непрерывна и
,
тогда система (1) определяет кривую y=f(x), где f(x)
непрерывна, f `(x) непрерывна и ![]() .
.
Пусть ![]() , тогда
в формуле
, тогда
в формуле 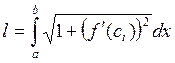 сделаем замену.
сделаем замену.
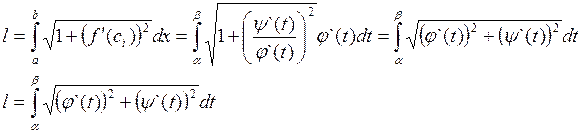
Замечание: Если кривая задана
пространственными координатами 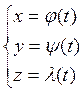 , то длина дуги
считается по формуле
, то длина дуги
считается по формуле 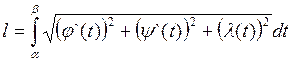
Пример: Вычислить длину астроиды
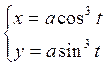
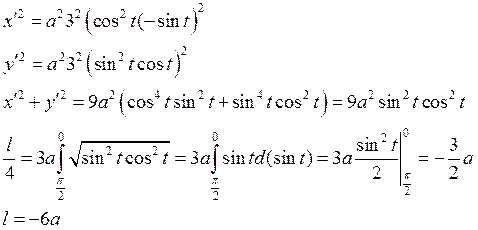
6) Длина дуги в полярной системе координат.
Пусть ![]() и
и ![]() меняется
меняется ![]()
![]()
х, у – декартовы
![]() и
и ![]() - полярные.
- полярные.
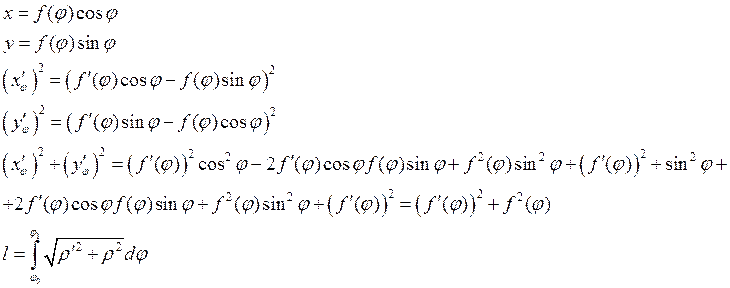
7) Вычисление объема тела по площади параллельного сечения.
Известно тело Т и известны площадь любого сечения плоскостью, перпендикулярной оси Ох.
![]() Пусть Q(x) есть непрерывная функция по х. Определить объем данного
тела.
Пусть Q(x) есть непрерывная функция по х. Определить объем данного
тела.
Проведем плоскости ![]() , где
, где ![]() .
.
Эти плоскости разобьют тело на
слои. В каждом промежутке ![]() выбирают точку
выбирают точку ![]() и на каждом промежутке строят цилиндрическое
тело образующая которого параллельна оси Ох, а направляющая есть контур сечения
тела Т плоскостью
и на каждом промежутке строят цилиндрическое
тело образующая которого параллельна оси Ох, а направляющая есть контур сечения
тела Т плоскостью ![]() .
.
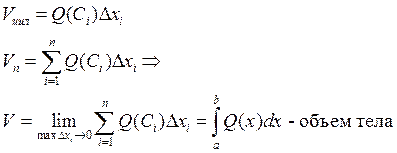
Физические приложения определенного интеграла.
1) Пусть под действием силы F материальная точка движется по прямой OS
и направление силы совпадает с направлением движения. Тогда работа производимая
силой F при перемещении материальной точки из положения
а в положение b, считается по формуле 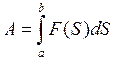 .
.

Пример: Какую работу надо затратить чтобы растянуть пружину на 7 см, если сила в 1 Н растягивает пружину на 1 см.
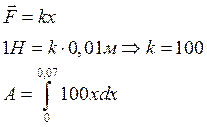
2) Вычисление пути.
Пусть точка движется по некоторой
линии и ![]() - ее скорость.
- ее скорость.
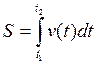 .
.
Пример:
![]()
t = 10 с
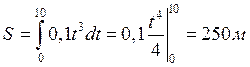
![]()
3) Координаты центра тяжести:
а) кривой АВ, заданной уравнением
y=f(x),
![]() , если линейная плотность кривой
постоянна, считаются по формуле
, если линейная плотность кривой
постоянна, считаются по формуле
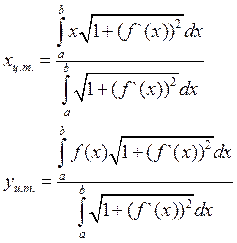
б) фигуры ограниченной прямыми
![]()
при условии что плотность фигуры постоянна считается по формуле
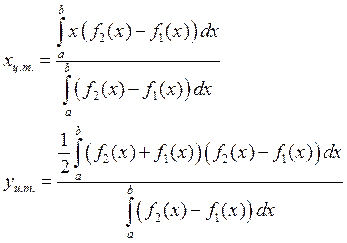
РЯДЫ
Числовые ряды.
Определение: Выражение вида ![]() называют числовым рядом.
называют числовым рядом.
![]()
Определение: числа ![]() называют членами ряда.
называют членами ряда.
Определение: Сумма n первых членов ряда называется частичной суммой ряда и
обозначается ![]() .
.
![]()
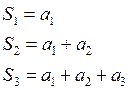
Если существует конечный предел ![]() , то ряд называется сходящимся рядом, а
число S – суммой ряда. Если же конечного ряда не
существует, то ряд называется расходящимся.
, то ряд называется сходящимся рядом, а
число S – суммой ряда. Если же конечного ряда не
существует, то ряд называется расходящимся.
Пример:
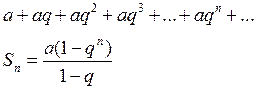
1) ![]() ,
тогда
,
тогда
![]() -
геометрическая прогрессия сходится по определению.
-
геометрическая прогрессия сходится по определению.
2) ![]()
![]() -
геометрическая прогрессия расходится.
-
геометрическая прогрессия расходится.
3) ![]()
а) ![]()

б) ![]()
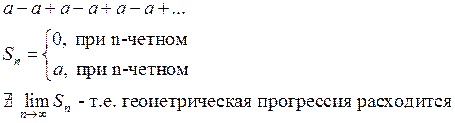
Теорема 1: Если сходится ряд получившийся из данного ряда отбрасыванием конечного числа ее членов, то сходится и данный ряд.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.