Производная неявной функции. Производная по направлению и градиент. Экстремум функции нескольких переменных, страница 5

1)

2)  и  - непрерывны на

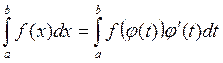3)  - определена и непрерывна на , то  (1)

Доказательство: Если F(x) – первообразная для f(x), то - первообразная для , тогда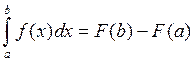

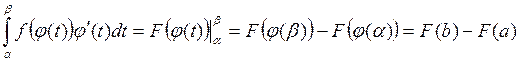
Замечание: При вычислении по формуле (1) к старой переменной не возвращаются, а пересчитывают в пределе.

Пример:

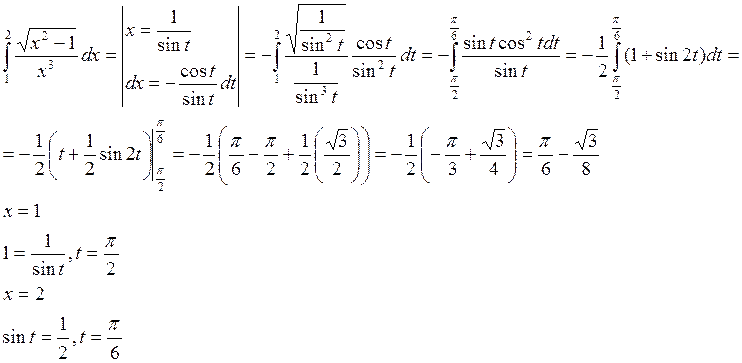
Интегрирование по частям в определенном интеграле.

Пусть u и v – дифференцируемые функции от х

Если  - первообразная для , то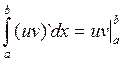

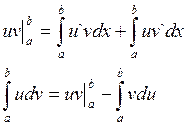
Пример:

Несобственный интеграл.

Два вида:

I.  Интеграл с бесконечными пределами.

II.  Интеграл от разрывной функции.

                          

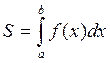
I. Интеграл с бесконечными пределами.

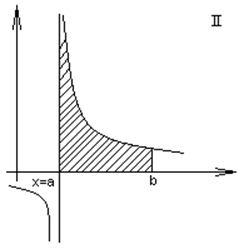
Пусть f(x) – определена  непрерывна при

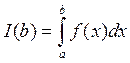 имеет смысл при b а..

Если существует конечный предел 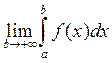, то этот предел называется несобственным интегралом от функции y=f(x) на интервале и обозначают .

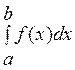 - сходящийся интеграл.

Если не существует конечного предела 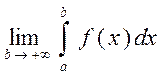 , то  - расходящийся интеграл.

Пример:

следовательно интеграл сходящийся.

Геометрический смысл: Пусть f(x)>0 при х>a.

 - выражает площадь неограниченной или бесконечной области, ограниченной линиями Ох, х=а, y=f(x).

Интеграл считается расходящимся, если хотя бы один из интегралов расходится.

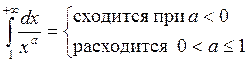
1) а=1

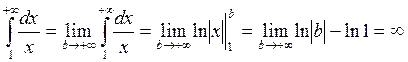 - расходится.

2) а>1

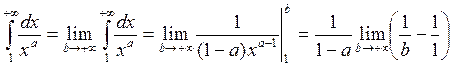 - расходится.

3) 0<a<1

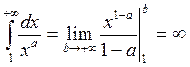 - расходится.

Теорема (Признак сравнения):

Пусть даны два интеграла I -  и II -  и пусть при всех выполняется неравенство , тогда

1)  из сходимости II следует сходимость I.

2)  из расходимости I следует расходимость II.

Вторая формулировка признака сравнения:

Если функции f(x) и не отрицательны и существует, конечный отличный от нуля предел не равный одновременно нулю и бесконечности, то интегралы I и II ведут себя одинаков, т.е. или оба сходятся или оба расходятся.

Пример:

 - сходится.

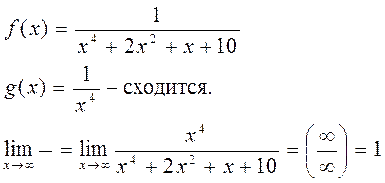
не равен 0 и не равен

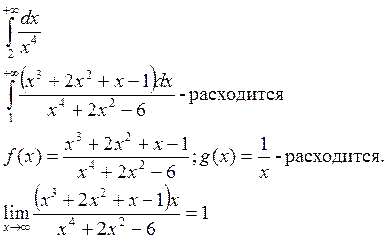
не равен 0 и не равен

Определение:

Интеграл , называется абсолютно сходящимся, если сходится .

Теорема: Если интеграл сходится абсолютно, т.е. , то интеграл - сходится.

Пример: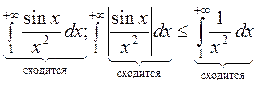

Интеграл от разрывной функции.

Пусть функция y=f(x) определена и непрерывна, на полуинтервале , а точке х=с функция либо неопределенна, либо терпит разрыв, в этом случае нельзя говорить об , как о пределе интегральных сумм, т.к. функция y=f(x) в точке С не непрерывна и этот предел может не существовать, по этому этот интеграл определяют как несобственный по следующей формуле:

.

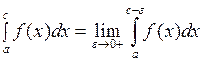Если правый интеграл существует, то его называют несобственным сходящимся интегралом, а в противном случае расходящимся интегралом.

Если функция y=f(x) не непрерывна при х=а, то .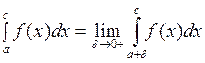

Если функция y=f(x) не непрерывна в точке , то

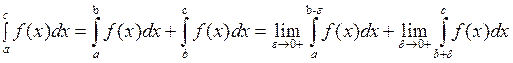
причем  сходится, если оба предела из правой части существуют.

Примеры:

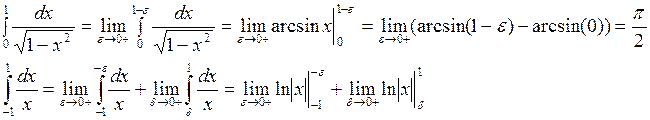
интеграл расходится.

Признак сравнения для несобственных интегралов от разрывной функции аналогичен признаку сравнения для несобственных интегралов с бесконечными пределами.

В качестве интегралов с которыми сравнивают рассматривают следующие интегралы:

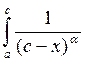 и 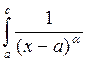, которые сходятся при  и расходятся при .

Интеграл по симметричному промежутку от четной и нечетной функций.

Рассмотрим интеграл .

1) Пусть функция y=f(x) четная, т.е. f(-x)=f(x).

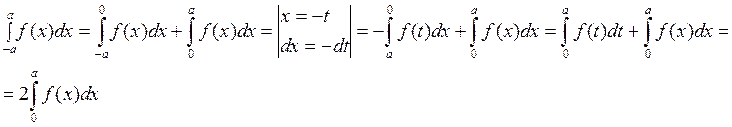
2) Пусть f(x)  нечетная, т.е. . f(-x)= -f(x).

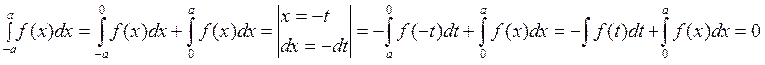
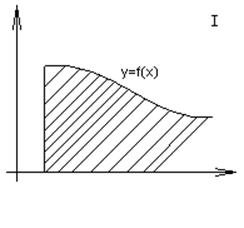
Геометрические приложения определенного интеграла.

1)  Площадь фигуры (если фигура задана в декартовых координатах).

Если на отрезке [a,b], функция f(x) не отрицательна, то площадь криволинейной трапеции считается по формуле .

Если же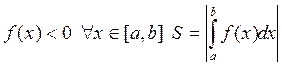

Если на отрезке [a,b] функция f(x), конечное число раз меняет знак, то отрезок [a,b] разбивается на частичные отрезки, на которых функция знакопостоянна и интеграл разбивается на сумму интегралов по частичным отрезкам.

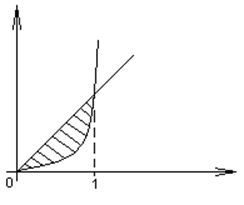
Пример:

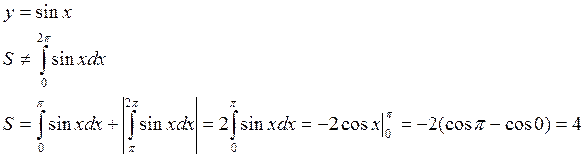
Если считают площадь области ограниченной линиями , прямыми х=а, х=b, при условии >, то .

Пример:

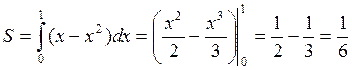
2) Площадь фигуры заданной в параметрической форме.