![]()
![]()

Подстановка:

Пример:
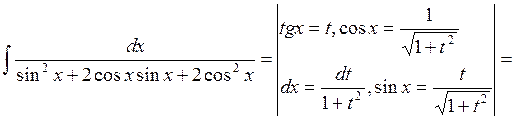
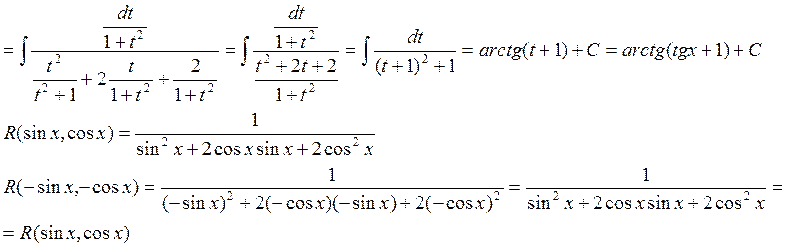 3) Подынтегральная
функция четна по синусу.
3) Подынтегральная
функция четна по синусу.
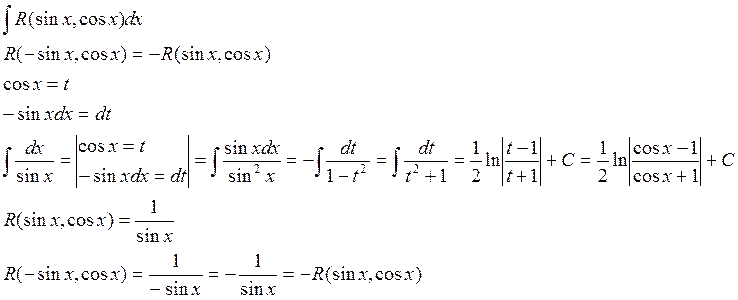
4) Подынтегральная функция нечетна по косинусу.
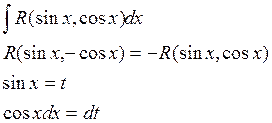
Пример:
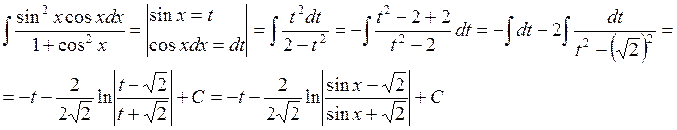
5) ![]()
Интеграл вида ![]() считается понижением степени по
формулам:
считается понижением степени по
формулам:
![]()
![]()
Пример:
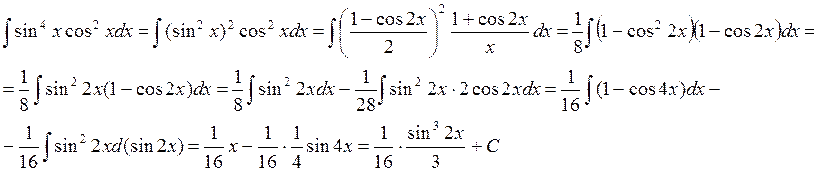
![]()
6) ![]()
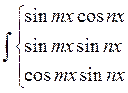
![]()
Преобразовывают подынтегральное выражение по следующим формулам:
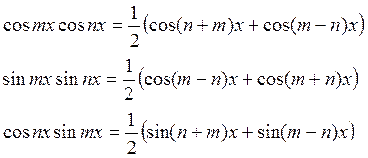
Пример:
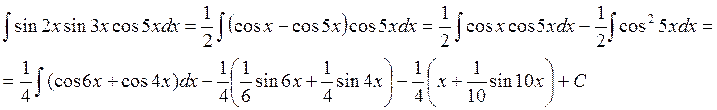
Интегрирование иррациональностей с помощью тригонометрической подстановки.
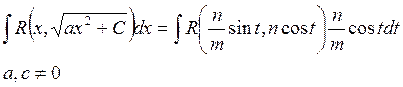
1) ![]()
![]()
Замена ![]() ,
,
![]() .
.
![]()
Пример:

2) ![]()
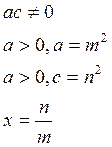
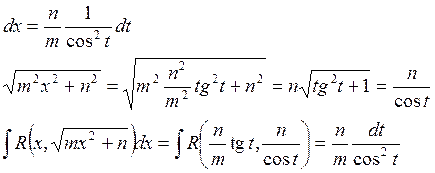
Пример:

3) ![]()

Пример:
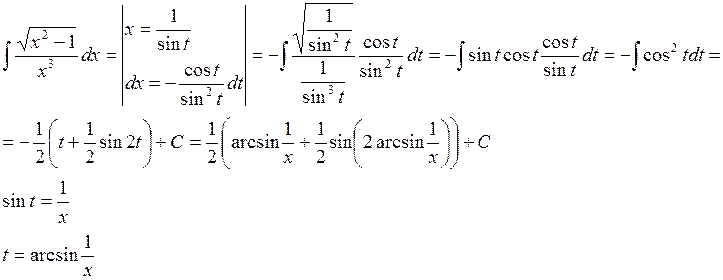
Интегрирование алгебраических иррациональностей.
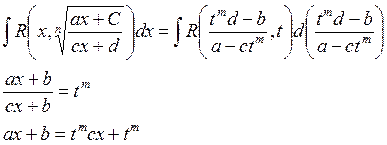
![]()
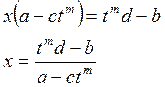
Пример:
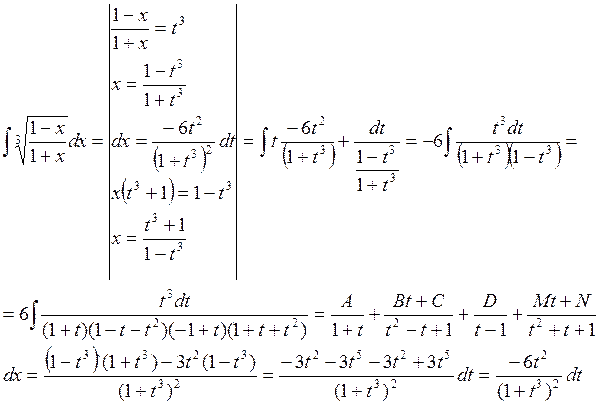
Интегрирование иррациональностей.
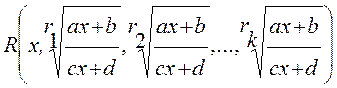
![]()
r – НОК (![]() )
)
Определенный интеграл.
Найти площадь
криволинейной трапеции ограниченной осью Ох, прямыми х=а, х=b,
y=f(x),
f(x) ![]() [a,b]
[a,b]

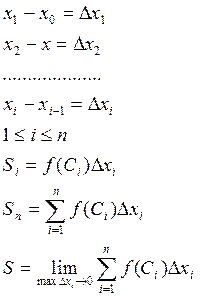
Пусть функция y=f(x) определена и непрерывна на отрезке [a,b]. Разобьем отрезок точками деления
![]()
На каждом
участке ![]() выберем точку
выберем точку ![]() и
составим сумму, называемую интегральной суммой. Если при любых разбиениях
отрезка [a,b]
и
составим сумму, называемую интегральной суммой. Если при любых разбиениях
отрезка [a,b] ![]()
![]() и при
любом выборе точек
и при
любом выборе точек ![]() интегральная сумма
интегральная сумма ![]() стремится к одному и тому же пределу
суммы, то этот предел называется определенным интегралом от функции f(x) на отрезке [a,b] и обозначается
стремится к одному и тому же пределу
суммы, то этот предел называется определенным интегралом от функции f(x) на отрезке [a,b] и обозначается 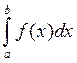 .
.
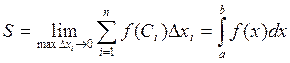
Число а называют нижним пределом интеграла, число b – верхним, отрезок [a,b] – отрезком интегрирования, х – переменной интеграла.
Если для функции f(x) существует предел интегральной суммы, то функция f(x) называется интегрируемой на отрезке [a,b].
Теорема: Если функции f(x) непрерывна на отрезке [a,b], то она интегрируема на нем.
Замечание 1:
При введении понятия определенного интеграла предполагалось, что a<b. В случае если b<a, то по определению полагали 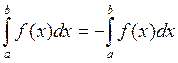 .
.
Заечание 2:
Если a=b, то все ![]() , следовательно
, следовательно 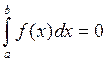 .
.
Свойства определенного интеграла.
1) Константу можно выносить за знак определенного интеграла.
Доказательство:
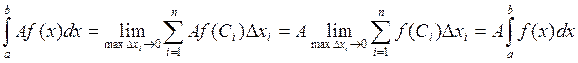
2) Определенный интеграл от алгебраической суммы функций равен алгебраической сумме определенных интегралов от слагаемых.
Доказательство:
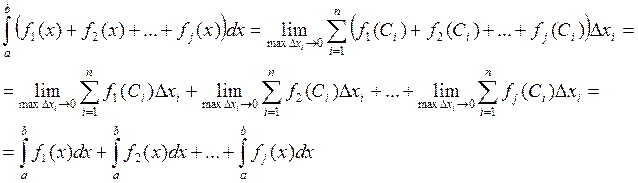
3) Если на отрезке [a,b], где a<b,функции f(x)
и ![]() таковы, что f(x)<
таковы, что f(x)< ![]() , то
, то 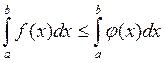 .
.
Доказательство: Рассмотрим 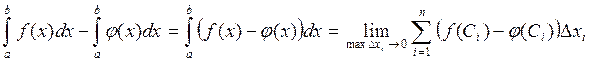
![]() , так
как
, так
как ![]() .
.
4) Если m и M наименьшее и наибольшее значение
функции f(x) на отрезке [a,b], и ![]() , то
, то 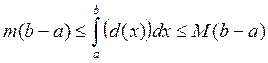
Доказательство:
![]() ,
,
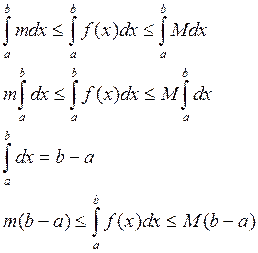
5) Теорема о среднем.
Если функция f(x) непрерывна на отрезке [a,b], то существует такая точка С на этом отрезке, такая что 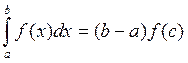 .
.
Доказательство: Пусть a<b, тогда из свойства (4),
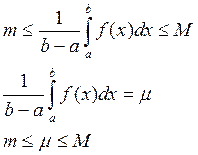
Так как функция f(x) непрерывна на отрезке [a,b], то она принимает на этом отрезке любые значения заключенные между наименьшим m и наибольшим M значениями. Следовательно
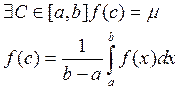
6) Для любых трех чисел a,b,c справедливо равенство  ,
если только эти интегралы существуют.
,
если только эти интегралы существуют.
Доказательство:
1. a<c<b.
Составим интегральную сумму для функции f(x) на отрезке [a,b], так как предел интегральной суммы не зависит от способа разбиения отрезка [a,b], на части, то разбивают отрезок [a,b] на малые отрезки так, чтобы С – была точкой деления, следовательно интегральная сумма составленная по отрезку [a,b], разбивается на 2 суммы, составленные по отрезку [a,с] и отрезку [c,b].
![]()
Переходя в последнем равенстве к
пределу при ![]() и получаем доказываемое равенство.
и получаем доказываемое равенство.
2. ![]() ,
тогда
,
тогда 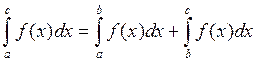 , следовательно
, следовательно
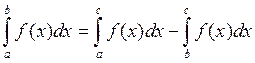 ,
следовательно
,
следовательно
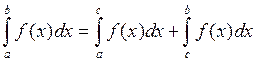
Формула Ньютона-Лейбница.
Рассмотрим интеграл  , в котором нижний предел а – закреплен,
а b – меняется, то интеграл функцией своего верхнего
предела
, в котором нижний предел а – закреплен,
а b – меняется, то интеграл функцией своего верхнего
предела 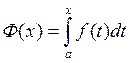 .
.
Теорема 1: Если f(x) непрерывная функция и 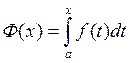 , то
имеет место равенство
, то
имеет место равенство ![]() .
.
Доказательство: 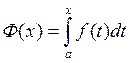 , дадим аргументу приращение
, дадим аргументу приращение ![]() .
.
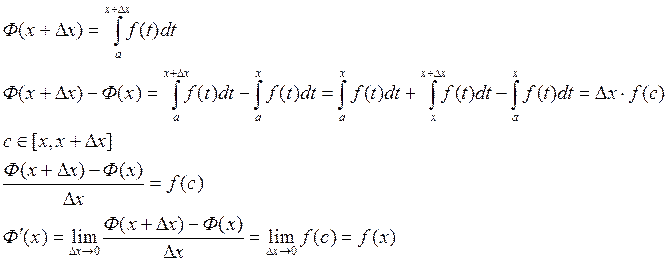
Теорема 2: Если F(x) есть какая-либо первообразная от f(x), то имеет место формула Ньютона-Лейбница 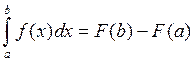 .
.
Доказательство: Пусть F(x) – первообразная. По теореме 1, 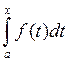 - первообразная, а две первообразные
отличаются
- первообразная, а две первообразные
отличаются 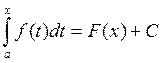 . Так как последнее равенство справедливо
при любых х, то оно справедливо при любых х=а и х=b.
. Так как последнее равенство справедливо
при любых х, то оно справедливо при любых х=а и х=b.
Пусть х=а 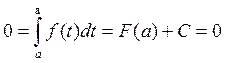
![]() ,
тогда
,
тогда 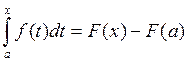 .
.
Пусть x=b 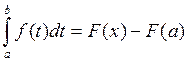 .
.
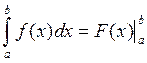
Пример:

Замена переменной в определенном интеграле.
Теорема: Пусть дан 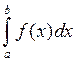 , где f(x) – непрерывна на отрезке [a,b] и
, где f(x) – непрерывна на отрезке [a,b] и ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.