Производная неявной функции. Производная по направлению и градиент. Экстремум функции нескольких переменных, страница 7

Обратная теорема: Если сходится данный ряд, то сходится и ряд получившийся из данного отбрасыванием конечного числа членов.

Доказательство: Пусть  - сумма первых n членов ряда,  - сумма k-отбрасываемых членов.

 - сумма членов входящих в  и не входящих в , тогда

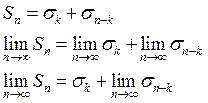
С точки зрения сходимости ряды ведут себя одинаково.

Теорема 2: Если ряд  сходится и его сумма равна S, то сходится и ряд (с=const) и его сумма равна cS.

Доказательство: Пусть  частичная сумма ряда , а  частичная сумма ряда .

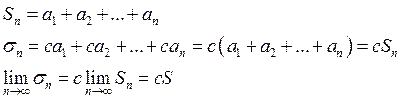
Теорема 3: Если ряды  и  сходятся и их суммы равны  и  соответственно то ряды  и , также сходятся  и их суммы равны  и .

Доказательство:

Пусть   - частичная сумма первого ряда

 - частичная сумма второго ряда .

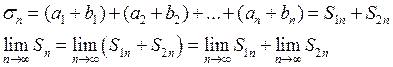
Правило: Сходящиеся ряды можно почленно складывать и вычитать.

Ряд и несобственный интеграл.

Теорема (Интегральный признак Коши): Пусть член ряда (1) задается равенством , если функция f(x) принимающая в точках х=n (n=1,2,…) значение f(n), монотонно убывает в некотором промежутке , то ряд (1) и несобственный интеграл 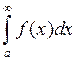 или оба сходятся или оба расходятся.

Доказательство: Изобразим члены ряда графически.

 равна сумме площадей построенных прямоугольников.

Площадь криволинейной трапеции ограниченной линиями

(2)

Рассмотрим правые прямоугольники.

Сумма площадей равна

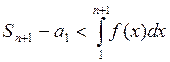(3)

Пусть интеграл 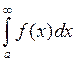 сходится, т.е. 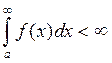, но 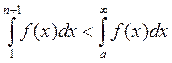; 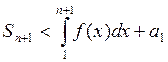, т.е. частичная сумма ограничена при всех значениях n и т.к. последовательность частичных сумм  возрастающая, то существует  следовательно ряд сходится.

Пусть интеграл 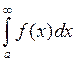 расходится, т.е. 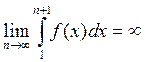, перейдем к пределу b не равному (2), получаем , получаем что  и ряд расходится.

Определение: Ряд  называется гармоническим рядом.

Гармонический ряд расходится.

Необходимый признак сходимости ряда

Теорема: Если ряд сходится, то .

Доказательство:

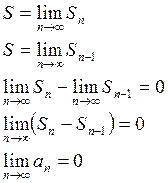
Из необходимого признака следует

 следовательно ряд расходится, а если , то ?!

Пример:

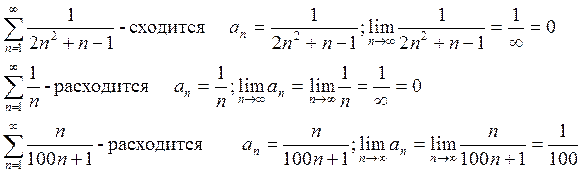
Достаточные признаки сходимости рядов

I. Признак сравнения:

(1)

(2)

Теорема 1: Пусть  для всех достаточно больших n, тогда из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда(2).

Теорема 2: Если существует конечный отличный от нуля предел , то ряды (1) и (2) ведут себя одинаково, т.е оба сходятся или оба расходятся.

Пример:

1)

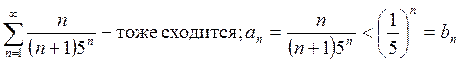
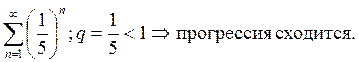
2)

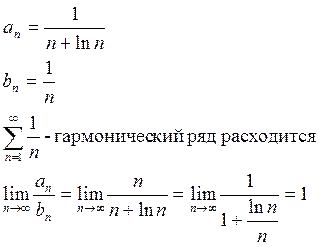
3)

Признак Даламбера

Теорема: Если существует предел , то

1)  l < 1 ряд сходится

2)  l>1 ряд расходится

3)  l=1 ряд может как сходится так и расходится

Доказательство:

1) Пусть l<1 (l<q<1)

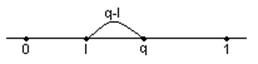
Из того что  следует, что .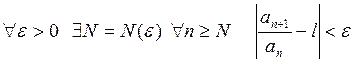

Пусть

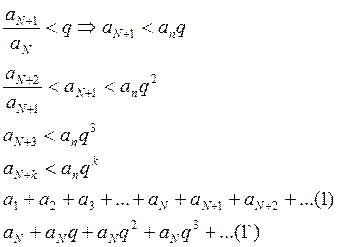
Ряд (1`) это геометрическая прогрессия со знаменателем q<1, поэтому ряд (1`) – сходится, но члены ряда (1), начиная с  меньше членов ряда (1`). На основании того, что конечное число членов ряда можно отбросить и признака сравнения следует, что ряд (1) сходится, как меньший ряд.

2) Пусть l>1, тогда начиная с некоторого номера N, отношение , следовательно , следовательно члены ряда  возрастают и не стремятся к 0, т.е  и ряд расходится по необходимому признаку.

Пример:

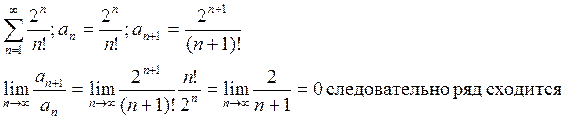
Теорема 3 (Радикальный признак Каши):

Если для ряда  существует предел , то при:

1)  l<1 – ряд сходится

2)  l>1 – ряд расходится

3)  l=1, ряд может как сходится, так и расходится.

Доказательство:

1) l<1 

 

Предположим   , тогда

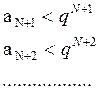
Ряд (2`) – геометрическая прогрессия со знаменателем q<1, поэтому ряд (2`) – сходящийся ряд, ряд (2) сходится, т.к. начиная с номера N его члены меньше, чем члены ряда (2`), а первые n-1 члены могут быть отброшены.

2) Пусть l>1. С некоторого номера N,  следовательно .

Пример:

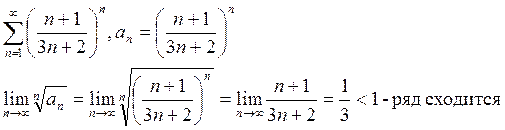
Знакопеременные ряды

Ряд называется знакопеременным, если среди его членов имеется как положительные так и отрицательные.

Ряды вида  называется знакочередующимся .

Теорема Лейбница: Если в знакочередующимся ряде (1), его члены таковы, что (2) и , то ряд (1) сходится его сумма положительна и не превосходит первого члена.